문제

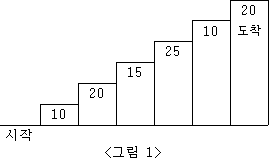
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.

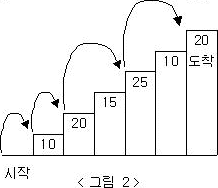
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

계단 오르는 데는 다음과 같은 규칙이 있다.

계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.

각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.

입력

입력의 첫째 줄에 계단의 개수가 주어진다.

둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.

출력

첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.

풀이

이 문제는 문제에서 주어진 요구 조건을 유의해서 풀어야 한다.

1. 한번에 한 계단, 두 계단 오를 수 있음
2. 연속된 세 개의 계단은 밟아서는 안됨
3. 마지막 도착 계단은 반드시 밟아야 함

이 3가지 조건을 생각하면서 규칙을 찾아보자.
d[N]은 N까지의 최대값, arr[N]은 N의 계단 값이라고 했을 때,
첫 번째 계단만 있을 경우 : arr[1]
두 번째 계단인 경우 : arr[1] + arr[2] , arr[2]
세 번째 계단인 경우 : arr[1] + arr[3] , arr[2] + arr[3]
네 번째 계단인 경우 : arr[1] + arr[2] + arr[4] , arr[1] + arr[3] + arr[4] , arr[2] + arr[4]

이와같이 진행되는데, 3번째 경우를 보면 첫 번째 계단에서 두 계단을 넘어간 경우와 두 번째 계단에서 한 계단을 오른 경우를 볼 수 있다.

마찬가지로 4번째 경우를 보면 2번째 계단에서 두 계단을 넘어간 경우와, 3번째 계단에서 한 계단을 오른 경우를 볼 수 있다.

여기서 더 자세히 들여다 보면, 문제에서는 최대값을 구하라 했으니 arr[1] + arr[2] 와 arr[2] 중 최대값을 이용할 것이고, 세번째 계단에서 하나 올라온 것이라면 그 전에는 조건2에 의해서 첫번째 계단(4번째 -3)에서 두 계단을 넘어선 다음 세번쩨 계단으로 올라온 것을 확인 할 수 있다.

즉, d[N]은 N-1번째에서 한 계단 올라온 경우와 N-2번째에서 두 계단을 올라온 경우 중 최대값을 저장하면 된다.

식으로 정리하면, d[N] = max(d[n-3] + arr[n-1] + arr[n], d[n-2] + arr[n]) 이라고 할 수 있다.

추가적으로 N=1인 경우도 유의해서 풀어야 한다.

소스

import java.util.*;

public class Main {
	public static int n;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		n = sc.nextInt();
		int[] arr = new int[n + 1];
		int[] d = new int[n + 1];

		for (int i = 1; i <= n; i++) {
			arr[i] = sc.nextInt();
		}

		d[1] = arr[1];
		if (n >= 2)
			d[2] = arr[1] + arr[2];

		for (int i = 3; i <= n; i++) {
			// 두 계단 뛰어서 올라오는 경우, 바로 아래 계단에서 올라오는 경우
			d[i] = Math.max(d[i - 2] + arr[i], d[i - 3] + arr[i - 1] + arr[i]);
		}

		System.out.println(d[n]);
	}

}