[Fourier Series and Fourier Transform] 1. Periodic Function and Fourier Series
Signal Analysis
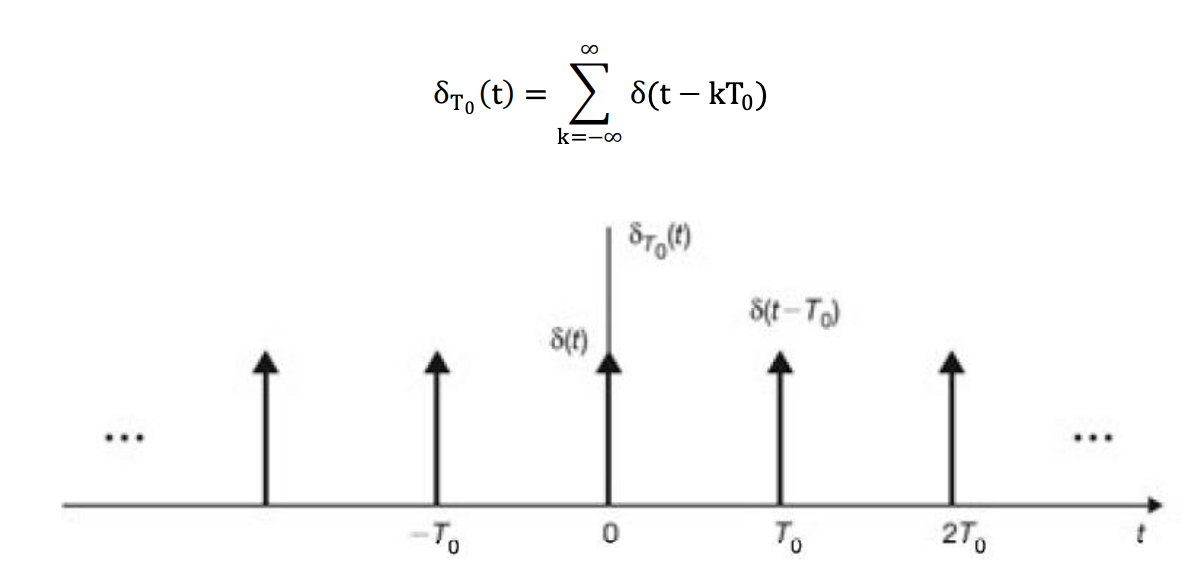
1. 주기함수
고등학교 과정을 마쳤다면,
위에서 제시한 함수 가 의 주기를 갖는 주기 함수라는 것은 한눈에 보고도 알 것이다.
자, 여기서 생각을 좀 더 해 보자.
를 만족하는 함수 는, 당연히 를 만족한다.
가 만족된다면,
를 만족하며,
이런 과정의 연속으로 주기 를 갖는 주기함수 에 대해,
라는 수식을 유도할 수 있게 된다.
그러나, 가 만약 과 같은 분수라면? 그럼에도 이 수식은 충족될 수 있을 것인가?
이에 대한 해답은 가장 간단한 주기함수인 삼각함수에서도 찾을 수 있다.
예를 들어, 는 의 주기를 갖는 주기함수이고, 에 대해서도, 에 대해서도, 그 주기성을 만족한다.
하지만, 나 와 같이,
주기의 정수의 배수가 아닌 경우에도 는 주기성을 만족하는가?
당연히 답은 '아니오' 이다. 너무나도 당연한 말로 들릴 지 모르겠지만,
주기함수는 그 정의에서 의 가 정수가 아니라면, 등식의 성립을 보장하지 않는다.
자, 그러나 조금 다르게 생각해 보자.
이라는 의 주기를 갖는 함수 가 있고,
, 라고 가정해 보자. 쉽게 말하여, 의 주기 는 의 주기 의 정수배이다.
함수 는 당연히 위에서 설명한 대로 를 충족한다.
자, 그런데 우리는 라는 사실을 기억해야 할 필요가 있다.
에 특정 정수를 곱할 시 의 주기 가 된다. 즉 는 의 주기인 를 주기로 갖는,
더 쉽게 표현하여, 로도 볼 수 있게 된다.
역은 성립되지 않지만, 우리는 와 동일한 주기를 갖는 함수로도 볼 수 있는 함수 를 구해내었다.
2. Fourier Series
오일러의 공식, 세상에서 가장 아름다운 수식으로도 잘 알려진 수식이다.
해당 수식을 유도해내기 위해서, 우리는 초월함수인 를 초등함수의 합으로 나타내는 "테일러 급수 (Talyor Series)" 를 사용하게 된다.
실제로 이렇게, 어떠한 수학적인 표현 (Mathematical Implementation) 을 또다른 관점에서 보기 위하여,
다른 함수들의 합, 곱 등의 다른 특정한 조합의 형태로 표현하는 일을 꽤 많이 하게 된다.
이번 장에서 다룰, Fourier Series 또한 이러한 "관점의 변환" 의 일환으로도 볼 수 있다.
무수한 수식으로 다루기 어려운 어떤 현상들을, 주기성만 가지고 있다면 주기함수의 합으로 관점을 변환시켜,
현상을 보다 쉽게 분석하게 할 수 있는 강력한 도구가 될 수 있다.
예를 들어 이러한 하나의 "현상" 을 보자.
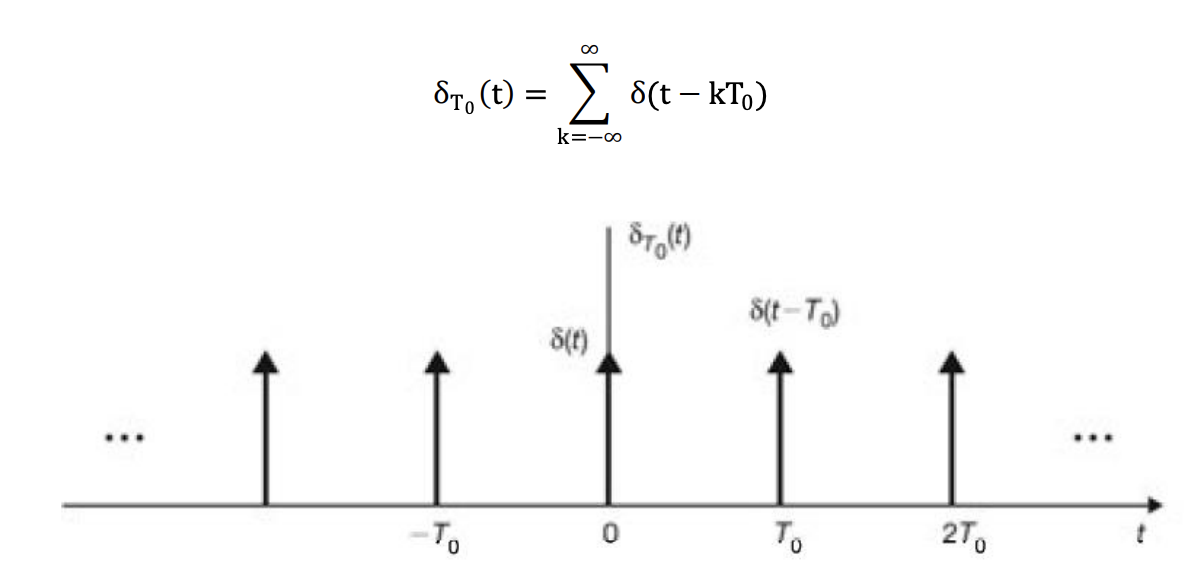
나중에 다시 한번 설명하겠지만, 이러한 현상을 우리는 "Impulse Train" 이라고 부른다.
Impulse Train이 무엇인가에 대해 알아보기에 앞서, 이러한 "현상" 을 우리가 수식으로 표현할 수 있는가?
물론 Impulse를 나타내는 표현인 가 있지만,
우리에게 익숙한 함수들인 나, / 등을 이용하여 표현해 낸다면,
이러한 Impulse Train을 주파수와 주기의 관점에서 분석할 때, 훨씬 더 편리할 것이다.
를 다루기 위한 특수한 방법 없이도 우리가 복소수나 삼각함수를 다루던 방법 그대로 다루면 되니까.
자, 그렇다면 어떻게 해야 하는가?
우리는 위에서 관점의 변화를 위하여, 하나의 수식을 다른 수식의 조합으로 "근사" 할 수 있다는 사실을 배웠다.
위의 Impulse Train은 주기 를 갖는 주기함수로도 표현될 수 있다.
이는, Impulse Train 은, 의 형식으로도 표현될 수 있다는 것이다.
위에서 배운 내용을 떠올려 보자.
함수의 "형태" 를 전혀 고려하지 않은 채, "주기" 의 관점으로만 함수를 바라봤을 때,
인 함수와, 의 주기 를 갖는 라는 함수를 떠올려 보면,
로도 결국 생각될 수 있다는 사실을 우리는 배웠다.
이러한, 과 같은 주기를 갖는 함수가 무한히 많다고 생각해 보자.
와 같이 표현될 수 있을 것이다.
우리가 가장 편하게 생각할 수 있는 주기함수는 다름아닌 복소수와 삼각함수이다.
이 둘을 각각 위의 방식으로 표현해 보면,
로 표현될 수 있다.
눈치가 빠른 분들이라면 벌써 필자가 무슨 말을 하고 싶은지 알아채셨을수도 있을 듯 하다.
그렇다. Impulse Train이라는 주기성을 가진 '낮선' 현상을, 친숙한 삼각함수와 복소수의 조합으로 다르게 표현하여,
분석에 훨씬 용이하게끔 만드는 하나의 "작업" 이 될 수 있는 것이다.
위의 두 수식이 바로, 오늘의 핵심 내용인 "Fourier Series" 에 해당하는 수식이다.
여기서 잠깐, Impulse Train과 삼각함수 및 복소함수는 주기성을 가진다는 것 이외에는,
전혀 닮은 점이 없는데 어떻게 저 둘이 같게 될 수 있냐 (등식이 성립하냐) 는 질문이 있을 수도 있다.
이러한 과정을 근사라고 부른다.
무한히 증가하거나, 감소한다는 하나의 '상태' 를 표현하는 기호인 를 통해,
현재 Fourier Series의 일환인 삼각함수와, 그 진폭들은 모두 다르며,
무수히 많은 삼각함수의 합으로 Fourier Series Expression은 Impulse Train에 무한히 "다가간다" 라는 표현을 사용한다.
쉽게 말하여, 주기함수의 특성을 활용하여 Impulse Train을 무수히 많은 삼각함수의 합으로 표현한 후,
무수히 많은 삼각함수의 합은 Impulse Train에 근접한다는 것을 보여주는 것이 바로 Fourier Series인 것이다.
