[Fourier Series and Fourier Transform] 2. Orthogonal Function

1. 내적 (Dot Product) 과 직교 (Orthogonal)

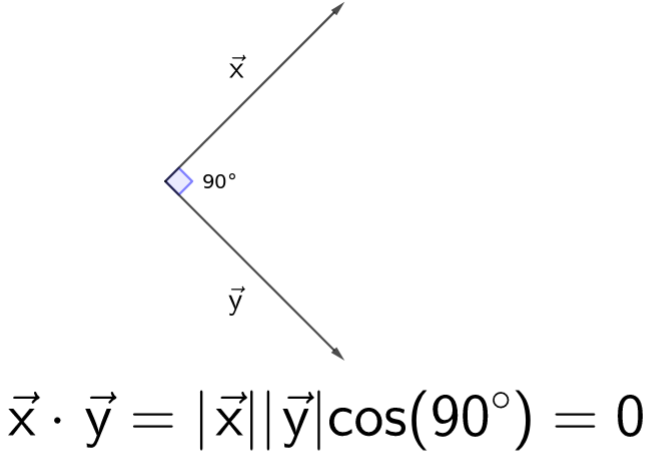
고등학교 기하와 벡터 과정에서 배우는 내용이다.
위의 사진과 같이, 두 벡터가 수직 관계에 있을 경우 두 벡터의 내적(Dot Product) 는 항상 0이 된다.

이 의미는 무엇인가. 대체 왜 0인 것인가? 단순히 $cos(\theta)$에서 $\theta$가 90 도라서?
무엇이 두 벡터의 "곱" 을 0으로 만드는 것인가?


자세한 설명에 앞서, Dot Product는, "종속적인 (Dependant)" 성분의 곱을 의미한다는 것을 먼저 말하겠다.
이해를 돕기 위하여 아래의 사진을 첨부하였다.

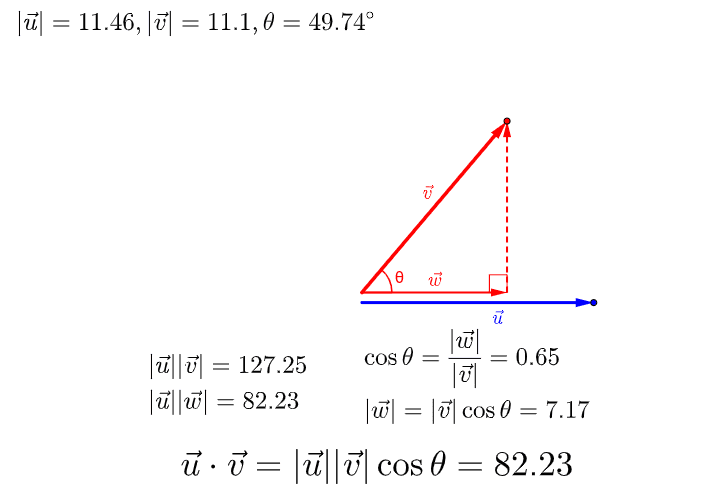
두 벡터 $v$와 $w$의 Dot Product를 나타낸 사진이다.

$v$를 Basis Vector의 합으로 볼 수도 있지만, $w$와 $w$에 수직하는 벡터의 합으로도 우리는 표현할 수 있다.
벡터를 하나의 "경로" 를 향한 직진으로 생각해 봤을 때, 어디로 가든 서울로만 가면 된다는 말처럼,

하나의 벡터는 무수한 벡터의 합으로 표현되어질 수 있다. 그 중 우리가 가장 많이 사용하는 것이 Basis Vector의 합일 뿐,
벡터는 다른 무수히 많은 벡터들의 합으로도 표현되어질 수 있다.

자, 벡터 $v$는, $w$와 $w$에 수직하는 벡터의 합으로도 표현될 수 있다고 위에서 말했다.
이를 우리는 벡터 $v$는 벡터 $w$에 해당하는 성분을 가진다고 표현한다.

(더 깊게 들어간다면 Vector Space를 이루는 조건에 대한 내용이 들어가게 된다.
여기까지 들어가는 것은 선형 대수의 내용이기에 이 글에서는 다루지 않겠다.)

더 표현해 보자면, 벡터 $w$는 벡터 $v$의 표현에 관여할 수 있다고도 필자는 말한다.
벡터 $w$와 이에 수직하는 벡터로 $v$를 표현해낼 수 있기에, $w$는 $v$의 표현에 관여할 수 있게 된다.


문제는 첫 번째 사진과 같은 경우이다. 벡터 $y$와 그에 수직하는 벡터를 활용하여 벡터 $x$를 표현해낼 수 있는가?
당연히 불가능하다. 벡터 $y$에 수직하는 벡터는 다름아닌 벡터 $x$이기 때문이다.

더 간단하게 말하여, 벡터 $x$는 벡터 $y$와 "아무 상관이 없는",
즉 벡터 $x$는 벡터 $y$에 종속적인 어떠한 성분도 가지지 않는다고 우리는 표현한다.


종속적인 성분이 단 하나도 없으니 당연히 종속적인 성분의 곱을 구해내는 Dot Product의 값은 0이 될 것이다.
이러한 관계를 수학에서는 '직교 (Orthogonal)'라고 표현한다. 겹치는 성분히 단 하나도 없게 되는 것이다.

2. 함수의 벡터 표현

아래의 아주 간단한 두 함수를 생각해 보자.

$y = x$
$y = 2x$


정의역에 손을 대지 않고, 위의 함수에서 아래의 함수를 만들어낼 수 있는가?
답은 당연히 Yes이다. 위의 함수의 모든 치역에 2를 곱해주기만 하면 아래의 함수가 되기 때문이다.

문제는, 저런 쉬운 1차함수가 아닌, 초월함수와 같은 형태가 나온다면 어떻게 될 것인가?
우리는 어떻게 $sin(x)$와 $cos(x)$가 서로 종속적인지 아닌지에 대해 판단할 것이며,

$e^{iw_0x}$와 $e^{iw_1x}$가 종속적인지 아닌지,
$\log{a_0}$와 $log{b_0}$이 종속적인지 아닌지 어떻게 판단할 것인가?


종속의 여부를 우리는 위에서 벡터의 Dot Product로 구해내었다.
Dot Product가 0이라는 것은, 서로가 서로에게 그 어떠한 성분도 종속되지 않음을 의미한다.

그렇다면 함수를 벡터로 표현할 방법은 없는 것인가?
벡터 함수가 아닌, 그냥 순수한 Linear Vector로 함수를 표현해내는 방법은 없는 것인가?


현대의 선형대수는 이에 대해 명확한 해답을 준다.
왜 굳이 벡터가 우리 눈에 보이는 2차원 혹은 3차원 공간에만 국한되어 있을 것이라 생각하는가?

함수를 무한대의 차원의 벡터로 표현해 보자.
아마 그 형태는 $(..., f(-2dx), f(-dx), f(0), f(dx), f(2dx), ...)$ 와 같은 형태가 될 것이다.

위에서 제시한 두 1차 함수 또한 이러한 벡터의 방식으로 표현될 수 있을 것이다.
각각 $v_0 =(..., -2dx, -dx, 0, dx, 2dx, ...)$ 와 $v_1 = (..., -4dx, -2dx, 0, 2dx, 4dx, ...)$ 로 말이다.

여기서, 벡터 $v_1$은 벡터 $2v_0$과도 같다.
이는 우리가 위에서 $y = x$의 모든 치역 원소에 2를 곱함으로서 $y = 2x$와 동일하게 만들 수 있다는 것을 보였다.

이는 벡터 $v_1$로 표현된 함수 $y = x$는, 벡터 $v_2$로 표현된 함수 $y = 2x$에 종속됨을 의미하며,
두 함수는 서로 겹치는 성분을 가짐을 의미하기도 한다.

3. 함수의 내적

함수를 "벡터" 라는 하나의 렌즈를 끼고 보고 있기에,
두 함수의 곱, 그러니까 $y = x$와 $y = 2x$의 모든 치역에 대한 곱은 여기선 "내적" 이 될 것이다.

이를 수학적으로 표현해 보면,

$f(x) = x, g(x) = 2x$

$\displaystyle\sum_{k = -\infty}^{\infty}f(x + kdx)g(x + kdx)$의 형태가 될 것이다.

즉, 무한소로 표현되는 각 함수의 모든 치역의 곱을 합한 것이다.
자, 여기서 시그마 기호와 $dx$ 기호를 보고 무언가 떠올려지는 것이 없는가?


바로 "적분" 이다.
위의 식은 표현하기에는 직관적이나 실제로 저 값이 0인지 아닌지에 대해 구해낼 길이 전혀 없다.

이를 해결하기 위해,
다시 말해 저 값이 실제로 0인지 아닌지에 대해 판단하기 위해, 우리는 이를 적분으로 표현해내게 된다.

$\displaystyle\int\limits_{-\infty}^{\infty}f(x)g(x)dx$ 와 같이 말이다.

실제로 위의 적분식은, 함수의 내적에 대한 공식이다.
위의 공식이 0이 된다면, 두 함수는 벡터 공간에서 서로 겹치는 성분이 없는 "독립"적인 성분이 되는 것이고,

0이 아닌, 발산 혹은 다른 값이 나온다면,
두 함수는 벡터 공간에서 서로 겹치는 성분이 있는 "종속" 적인 성분이 되는 것이다.

4. 우함수와 기함수의 직교

$f(x) = f(-x)$
$f(x) = -f(-x)$

각각 우함수 (Even Function)와 기함수 (Odd Function) 에 대한 조건 표현이다.
우함수인 함수와, 기함수인 함수는 서로 직교하게 된다.

잠시 생각을 해 보자. 하나는 $y$축을 중심으로 대칭되고, 하나는 원점을 중심으로 대칭되는 함수이다.
어떻게 $y$축 대칭의 함수를 원점 대칭으로 만들 것인가? 그 반대는 또 어떻게 할 것이고?

우함수인 함수를 백날 더해 봤자 결국 우함수이다. 마찬가지로 기함수인 함수를 백날 더해 봤자 결국 기함수이다.
이는 아래의 계산으로 깔끔하게 보여질 수 있다.

$f(x) = f(-x)$
$g(x) = -g(-x)$

$f(x)g(x) = f(-x) \times(-g(x)) =-f(-x)g(-x)$

$\displaystyle\int\limits_{-\infty}^{\infty}f(x)g(x)dx$

$= \displaystyle\int\limits_{0}^{\infty}f(x)g(x)dx + \displaystyle\int\limits_{-\infty}^{0}f(x)g(x)dx$

$= \displaystyle\int\limits_{0}^{\infty}f(x)g(x)dx - \displaystyle\int\limits_{0}^{\infty}f(x)g(x)dx$

$= 0$

다시 말해 우함수는 기함수인 성분을 가지지 않으며,
기함수 역시 우함수인 성분을 전혀 가지지 않고, 둘은 직교한다고 볼 수 있다.