3. Line Search Methods

1. 개요

본격적인 최적화 기법으로 넘어가 보도록 하겠습니다.

3장은 앞서 몇 번 언급된 Line Search 기법입니다.

아래의 식과 같이, Search Direction $p_k$의 방향으로 $\alpha_k$(Step Length)만큼 이동해가며, $x$값을 계속 갱신해 나가며, 최적값을 찾는 방식입니다.

$x_{k+1}=x_k+\alpha_kp_k$

책에서는 방향을 의미하는 $p_k$가 decent direction으로 가야 된다고 언급하고 있습니다. $x$값이 수렴을 해야 하니 당연한 말입니다. 중요한 부분은 다음 수식입니다.

$p_k=-B_k^{-1}\nabla f_k$

사실 위의 수식에서 $B_k^{-1}$부분은 생략되어서, $f$의 미분 값으로만 최적화를 하는 것도 가능은 합니다. 하지만, 수렴 속도나 정밀도 등을 고려할 때, $B_k^{-1}$를 제어하는 것이 필요합니다.

1.1 예제

예제를 가지고 한번 설명해보겠습니다.
아래의 $f(x)$를 최적화를 해보겠습니다.

$f(x)=0.01x^4-0.03x^3-0.45x^2+0.3x-1$

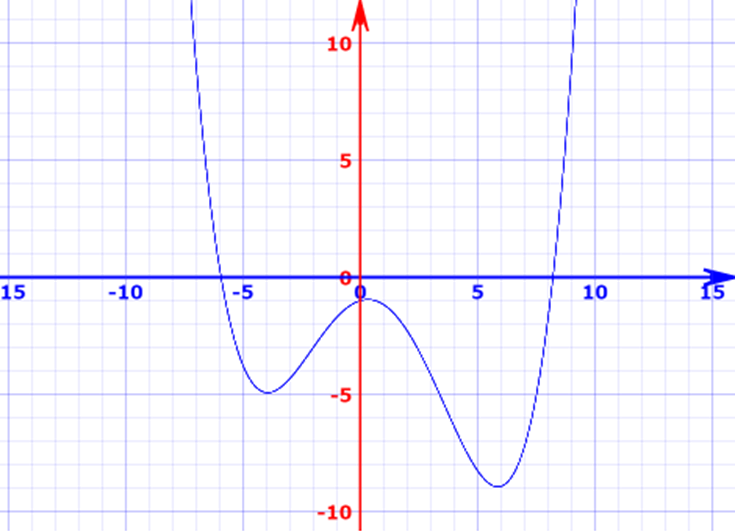
이 함수의 형태는 아래와 같습니다.
대략, $x=6$근처에서 최적값이 존재하는 것을 볼 수 있습니다.

여기서는 간단하게 위의 $B_k^{-1}$는 1이라고 하겠습니다.

그럼, $p_k=-\nabla f_k$이며, $\nabla f_k=0.04x_k^3-0.09x_k^2-0.9x_k+0.3$ 입니다.

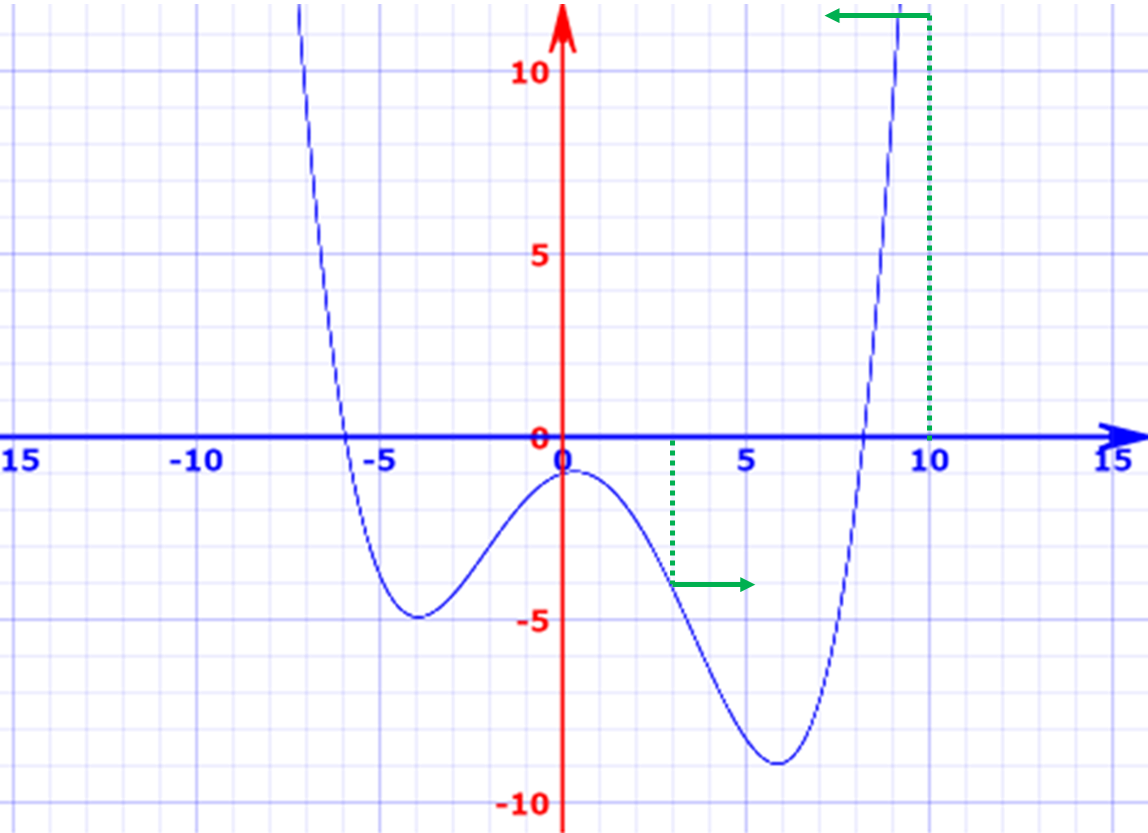
$x_k=10$, $x_k=3$인 경우를 보면 각각, $\nabla f_k$값은 22.3, -2.13 이며, $p_k$는 -22.3, 2.13입니다. 여기서 $p_k$는 decent direction이 되어야 한다는 의미를 보면, $x_k=10$인 경우를 보면, 최적이 되기 위해서는 x가 감소를 해야 합니다. 이를 위해서는 방향이 (-)로 가야 합니다. -22.3의 (-)부호가 그 의미입니다. 반대로 $x_k=3$인 경우는 최적으로 가기 위해서는 증가를 해야 합니다. 2.13 즉 양의 값을 가지는 의미입니다.

시작점 $x_0=10$, Step Length $\alpha$를 0.01로 두고 한번 코드를 짜보겠습니다.

class LineSearchIntro
{
private:
	static double nextX_k(double x_k)
	{
		double derivF = 0.04 * x_k * x_k * x_k - 0.09 * x_k * x_k - 0.9 * x_k + 0.3;
		double p_k = -derivF;
		double stepLen = 0.01;

		return x_k + p_k * stepLen;
	}

public:
	static double getSolve(double init_x)
	{
		double prev = init_x;

		while (true)
		{
			double next = nextX_k(prev);

			if(abs(prev - next)<0.001)
				break;

			prev = next;
		}

		return prev;
	}
};

    double sol = LineSearchIntro::getSolve(10.0);

위의 코드에서 getSolve를 보면 while문을 통해 계속 x의 값을 업데이트 하는 것을 볼 수 있으며, 이전 값과의 변화가 0.001이하이면 종료하도록 했습니다. 이 작업을 iteration이라고 합니다.

그리고 실제 x를 업데이트 하는 nextX_k메소드를 보면, $x_{k+1}=x_k+\alpha_kp_k$, $p_k=-\nabla f_k$ 2개 수식에 의해서 업데이트 되고 있습니다.

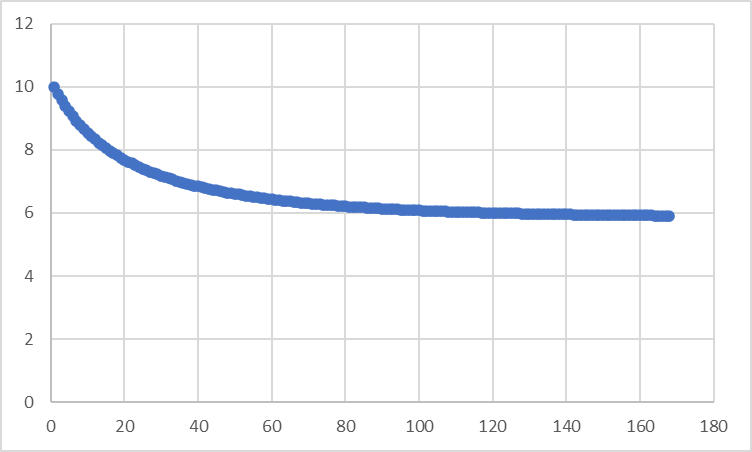
결과를 보면 5.9118835346333682로 위 그래프에서 보듯이 6근처의 값이 나옵니다. 그리고 x값의 변화를 보면, 아래 그래프와 같습니다.
약 170번 정도 iteration을 하며 Solution으로 수렴해 가는 것을 볼 수 있습니다. 앞으로 우리가 해야 하는 모든 작업은 이 그래프 같이 결과가 수렴하도록 해야 하는 것입니다.

이번에는 반대로 시작점 $x_0=-6$으로 해보겠습니다.

    double sol = LineSearchIntro::getSolve(-6.0);

약 180회의 iteration을 거쳐 결과는 -3.9998828942235911이 나옵니다. 이는 위의 그래프에서 좌측의 Local Optimization을 찾은 경우가 됩니다. 시작 위치에 따라서 결과가 크게 달라지는 것을 볼 수 있습니다.

이해하기에 도움이 되는 예제지만, 실무에서는 절대 못 만날 예제입니다...

2. Step Length

앞서 예제를 보면, Step Length ($\alpha$)를 임의로 0.01로 두었고, 이 때 Iteration횟수는 170회 정도였습니다. 경우에 따라서 다르기는 하겠지만, Iteration이 100회를 넘어가는 건 그렇게 좋은 경우는 아닙니다.
예제와 같이 단순한 문제에서는 이 원인은 Step Length가 너무 작았기 때문엡니다. 하지만 무작정 Step Length를 키우지도 못하는데 그 이유는 자칫 수렴도 아니고 발산도 아니고 핑퐁을 치는 (steady state에 도달하지 못하는) 상태가 되어 버릴 수도 있습니다.

그래서 Step Length를 결정하는 몇 가지 기법에 대해 설명합니다.
사실 기법이라기 보다는 분석에 더 가깝지 않을까 싶습니다. 이 방법도 결국은 임의 선택의 순간이 있기 때문입니다. 단지 이런 기법을 통해서 조금 더 논리적으로 Step Length를 찾아보는데 의미가 있다고 할 수 있습니다.

2.1. Wolfe Condition

Step Length 를 결정하기 위한, 기법도 복수가 존재하나
대표적인 wolfe condition에 대해서만 간략하게 언급하겠습니다.

수식적 구성은 아래와 같습니다.

첫 번째가 일반적인 wolfe condition이고, 두 번째가 strong wolfe condition입니다. 여기서 중요한 점은 step length가 k에 따라 다를 수 있습니다. 즉 iteration마다 업데이트 될 수 있다는 의미입니다.

$f(x_k+\alpha_kp_k) \leq f(x_k)+c_1\alpha_k\nabla f_k^Tp_k,$
$\nabla f(x_k+\alpha_kp_k)^Tp_k \geq c_2\nabla f_k^Tp_k$
$0<c_1<c_2<1$

Strong condition을 보면 2 번째의 등호 방향이 반대인 것을 볼 수 있읍니다.
이 말은 양 변이 음(-)의 값을 가지는 경우에 만족할 수 있습니다.

$f(x_k+\alpha_kp_k) \leq f(x_k)+c_1\alpha_k\nabla f_k^Tp_k,$
$|\nabla f(x_k+\alpha_kp_k)^Tp_k| \leq c_2|\nabla f_k^Tp_k|$
$0<c_1<c_2<1$

수식으로만 보면 이해가 잘 안될 수 있으니 그림을 보겠습니다.

위의 예제에서
$x=-2.5$인 경우, $c_1=0.1, c_2=0.5$로 두고 $\alpha$를 x축으로 하여 그래프를 그려보면 아래와 같습니다.

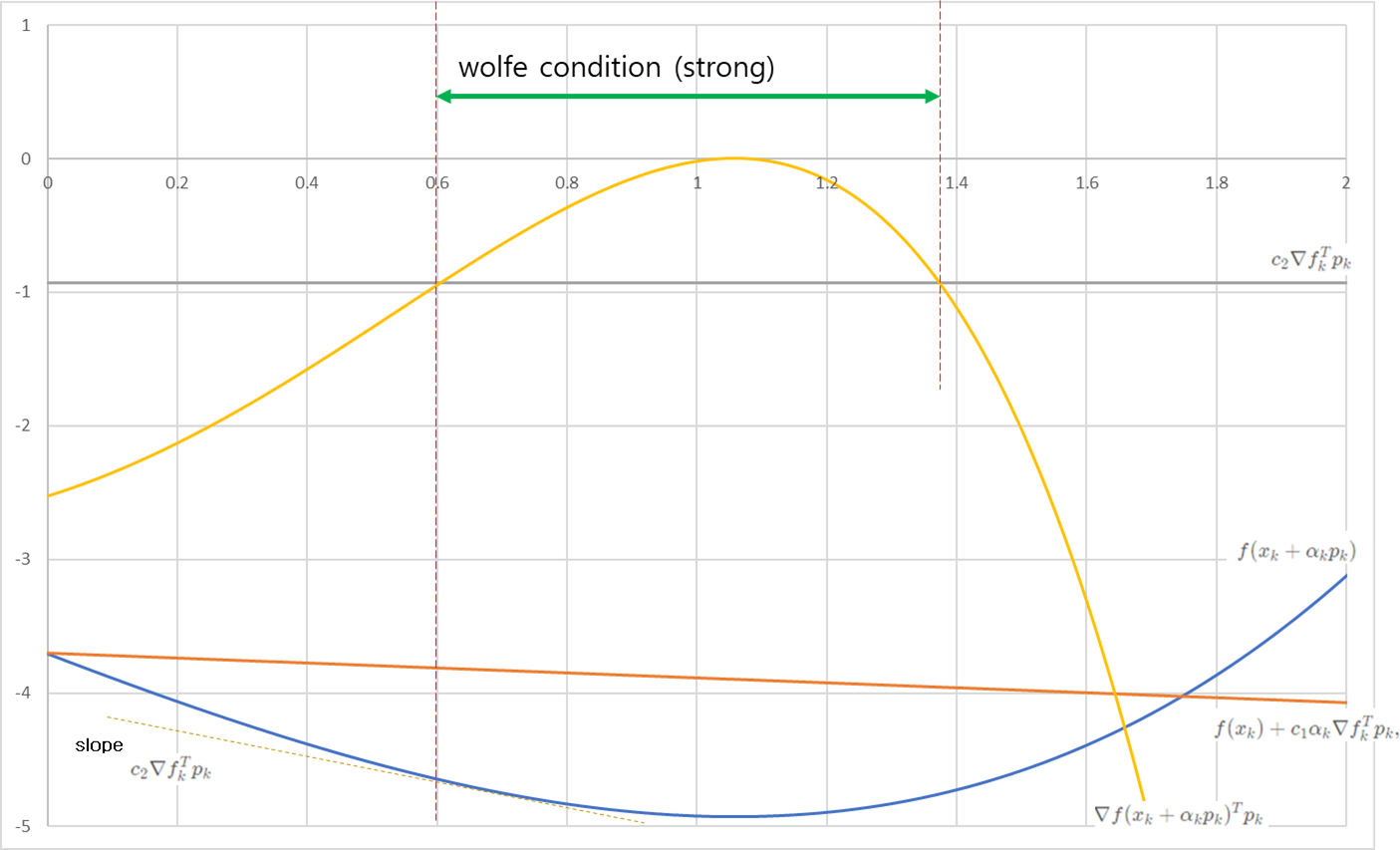
파란색 라인이 $f(x_k+\alpha_kp_k)$이고, 주황색 라인이 $f(x_k)+c_1\alpha_k\nabla f_k^Tp_k$ 입니다. 위의 첫 번째 조건을 만족하는 $\alpha$는 $0\leq\alpha \leq 1.73$ 입니다.
이 구간 내에서 두 번째 조건을 만족하는 구간은 $0.61\leq\alpha \leq 1.37$ 입니다. 이 예제에서는 이 구간은 strong condtion도 동시에 만족합니다. 즉 step length는 이 사이의 값을 사용하면 됩니다.

눈 여겨볼 부분은 $c_2\nabla f_k^Tp_k$ 값입니다. $p_k$가 $f$의 미분값이기 때문에 이는 2차 미분에 해당합니다. 그래서 curvature condition이라고도 부르며, 이 값을 기울기로 하는 직선이 $f(x_k+\alpha_kp_k)$ 만나는 지점, 즉 $f(x_k+\alpha_kp_k)$의 미분 값이 $c_2\nabla f_k^Tp_k$인 지점이 두 번째 조건을 만족하는 위치이기도 합니다.

이 외에도 Goldstein condition이라는 방식도 존재하는데, 개념 자체는 크게 다르지않습니다.

2.2. Wolfe Condition 예시

위의 예제에서 Wolfe Condition을 적용해보겠습니다.

기존 nextX_k의 stepLen을 0.01로 고정했으나,
findStepViaWolfeCondition이라는 메소드에서 Wolfe Condition을 이용하여 찾도록 했습니다.

        static double nextX_k(double x_k)
	{
		double derivF = 0.04 * x_k * x_k * x_k - 0.09 * x_k * x_k - 0.9 * x_k + 0.3;
		double p_k = -derivF;
		//double stepLen = 0.01;
        double stepLen = findStepViaWolfeCondition(x_k, derivF);
		return x_k + p_k * stepLen;
	}

원할한 계산을 위해서 $f$와 $\nabla f$를 계산하는 메소드를 따로 만들고
findStepViaWolfeCondition 을 구현했습니다.
여기에도 일종의 최적화 기법이 들어가야 하는데, 간단히 step이 0.0에서 0.01씩 증가해가며, 조건을 만족하는 step length를 찾도록 했습니다.

	static double func(double x_k)
	{
		double f = 0.01 * x_k * x_k * x_k * x_k - 0.03 * x_k * x_k * x_k - 0.45 * x_k * x_k + 0.3 * x_k - 1.0;
		return f;
	}

	static double derivFunc(double x_k)
	{
		double derivF = 0.04 * x_k * x_k * x_k - 0.09 * x_k * x_k - 0.9 * x_k + 0.3;
		return derivF;
	}

	static double findStepViaWolfeCondition(double x_k, double derivF)
	{
		double c1 = 0.1;
		double c2 = 0.5;

		double p_k = -derivF;
		double slop = -c2 * derivF * derivF;

		double step = 0.0;
		double x = 0.1;
		while (true)
		{
			//f(x_k+\alpha_kp_k)
			double f_x_ap = func(x_k + step * p_k);
			//f(x_k)+c_1\alpha_k\nabla f_k^Tp_k
			double f_x = func(x_k) + c1 * step * derivF * p_k;
			//\nabla f(x_k+\alpha_kp_k)^Tp_k
			double derF_p_k = derivFunc(x_k + step * p_k) * p_k;
			//$c_2\nabla f_k^Tp_k$
			double c2_derF_p_k = c2 * derivF * p_k;

			//Strong Condition
			derF_p_k = abs(derF_p_k);
			c2_derF_p_k = abs(c2_derF_p_k);

			
			if (f_x_ap > f_x || derF_p_k > c2_derF_p_k)
			{
				step += 0.01;
				continue;
			}
			else
				break;
		}
		
		return step;
	}

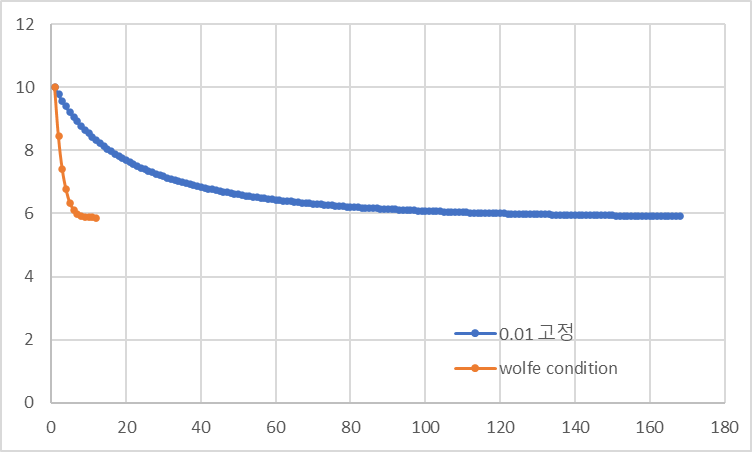
$x_0=10$인 경우에 결과를 보면, Wolfe Condition을 적용(Iteration 12회)했을 때, 고정했을 때(Iteration 168회)와 달리 10배 이상 빨리 수렴하는 것을 확인할 수 있습니다. 물론 조건에 따라 다르며, 추가적으로 step length를 찾는 부분이 들어갔기 때문에 리소스는 더 소모됩니다. 즉 trade off가 발생하기 때문에 적당한 선을 찾아야 합니다.