Numerical Optimization

위의 책은 공학 문제에 있어, 가장 중요한 요소인 최적화(Optimization)에 관한 일종의 교재입니다. 공학계열의 석사 과정 이상을 밟는다면 꼭 한번 쯤 다뤄야 하는 주제로 생각되고, 현업에서도 저와 같은 Engineering 알고리즘 개발자는 꼭 알아야 하는 내

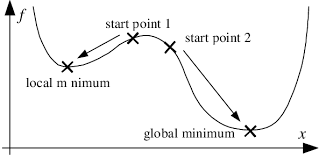
첫 장은 소개이므로, 간단히 요약 정리하는 수준으로 적어볼 예정입니다. Optimization 최적화를 하기 위해서는 먼저 Objective(목적)를 정의해야 됩니다. 이 용어는 Cost(비용), Energy와 같은 단어로 표현됩니다. 저는 개인적으로 Cost를 많이

2장 입니다. 2장 역시 간단한 개념 소개를 하기 때문에 간략하게 언급하는 정도로 넘어가겠습니다. 용어 정도 알고 넘어가는 정도면 되겠네요. 1. Solution이란 Solution, 우리 말로는 해를 말합니다. 책에서는 1장에서도 언급된 개념인 Global 과 L

개요 Linear Solver라고 하면, 통상 $Ax=b$ 형태의 수식에서 $x$를 구하는 방법을 말함. 여기서 $A$와 $b$는 matrix의 형태가 될 수 있으며, $A$가 $(m\times n)$일 때, $b$는 $(m\times 1)$, $x$는 $(n\tim

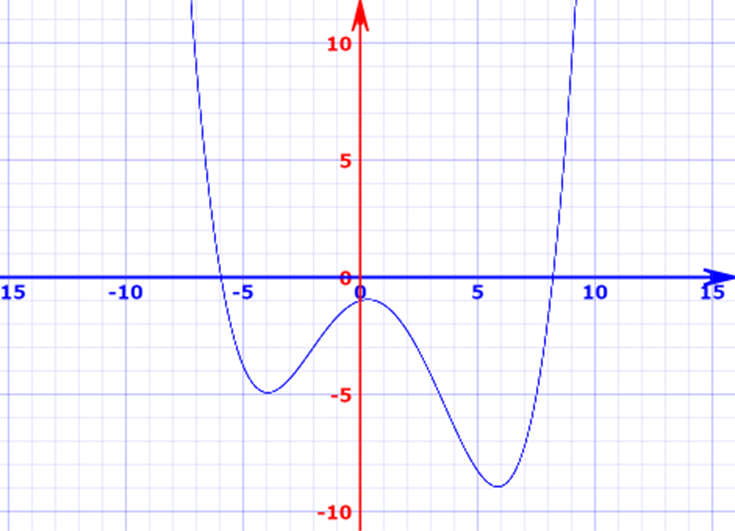
본격적인 최적화 기법으로 넘어가 보도록 하겠습니다. 3장은 앞서 몇 번 언급된 Line Search 기법입니다. 아래의 식과 같이, $pk$의 방향으로 $\alphak$(Step Length)만큼 이동해가며, $x$값을 계속 갱신해 나가며, 최적값을 찾는 방식입니다

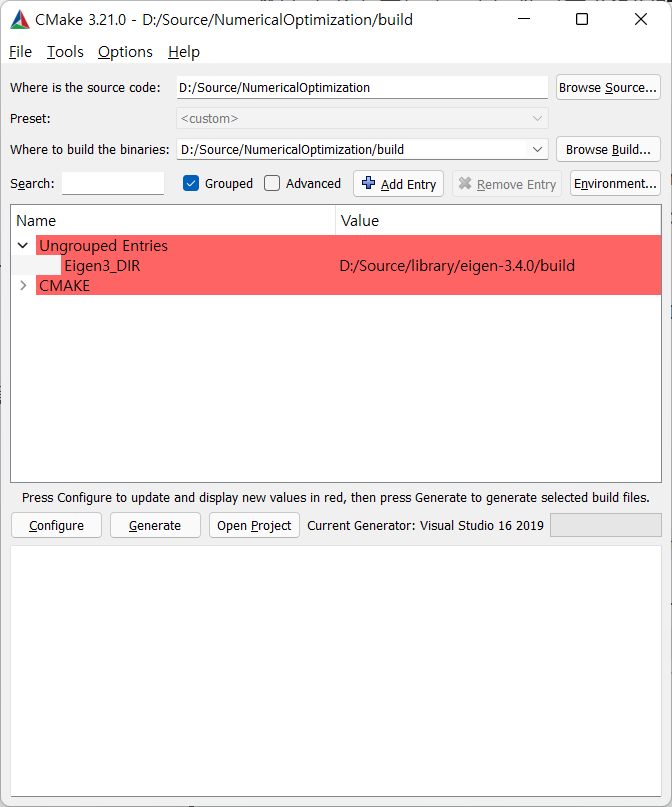
Optimization코딩을 위해서는 Linear Algebra용도의 라이브러리가 반드시 필요합니다. 직접 짤 수도 있겠지만, 여기서 설치할 Eigen의 경우는 제공되는 기능이나, 성능적으로 충분히 최적화되고 안정화된 라이브러리이기 때문에 Eigen 사용을 권합니다.

True Region기법은 큰 틀에서 본다면, Line Search와 유사합니다.다만, Cost Function($f$)를 그대로 사용하는 것이 아니라,유사한 Model Function($m$)으로 근사하여, 최적화를 수행하며,동시에 일정한 Bound내에서 Model