코딩테스트

문제 1.

1 ~ n 까지의 숫자 중 소수 (1 과 자기자신으로만 나누어지는 수) 를 출력하는 코드를 작성해보자.

1. 하나씩 다 확인해보는 방법

def solution(x):
    x=100
    a =[]
    for j in range(2,x+1):
        check = 0
        for i in range(2,j):
            if j % i == 0:
                check = 1
        if check == 0:
            a.append(j)
    return a

2. 에라토스테네스의 체

def prime_list(n):
    # 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
    sieve[n] = [True] * n
# i=sqrt(n)까지 검사
    m = int(n ** 0.5)
    for i in range(2, m + 1)
        if sieve[i] == True:           # i가 소수인 경우
            for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
                sieve[j] = False
 # 소수 목록 산출
    return [i for i in range(2, n) if sieve[i] == True]
    

에라토스테네스는 자연수 중에서 소수를 가려내는 방법을 고안했다. 예를 들어 50이하의 소수를 찾아보자.

1단계 : 1~50까지의 수를 나열해보자.

2단계 : 먼저 소수도 합성수도 아닌 1을 지운다.

3단계 : 2는 약수가 자기자신과 1뿐인 가장 작은 소수가 됩니다. 방금 찾은 소수 2를 제외한 2의 배수는 체에 거르듯이 모두 지운다. 아래 그림에서는 주황색으로 지웠다.

4단계 : 이제 남은 수들 중 가장 작은 수인 3을 보니, 소수임을 확인할 수 있다. 이제 3을 제외한 3의 배수를 모두 지운다. 아래 그림에서 파란색으로 지웠다.

5단계 : 그 다음 수인 5도 소수이므로 5를 제외하고 5의 배수도 지우고, 그 다음 소수인 7을 제외한 7의 배수도 지운다. 아래 그림에서 각각 초록색 동그라미와 빨간색 세모로 지웠다.

6단계 : 계속 반복한다.

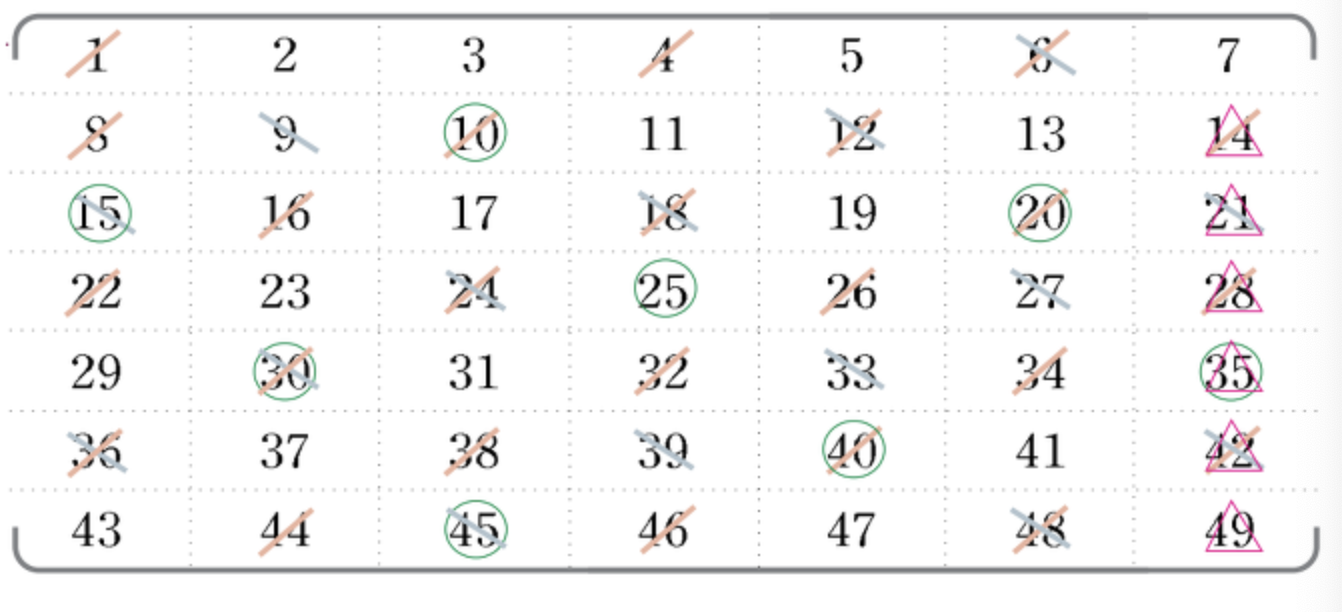
이렇게 에라토스테네스의 체를 거르고 나면 남은 숫자들은 소수가 남게된다.

잠깐 생각해볼것 ! 왜 여기에서는 하필 7까지 밖에서 살피지 않았는데도 모든 소수를 구할 수 있었을까? 굳이 47까지 확인을 하지 않아도 되는 이유는 무엇일까?

바로 7의 제곱이 50과 가까운 49이기 때문이다. 50이 2의 배수임을 감안하고 2의 배수들을 지워나갈 때, 50을 소수가 아님을 (체에 걸러짐을) 예상할 수 있다. 그럼 우리는 49까지의 숫자에서 소인수를 생각해보면 된다. 만약 49이하의 어떤 수가 a * b 로 소인수분해 된다고 한다.

만약 a 가 7보다 더 큰 소인수라면, b는 7보다 작은 소인수여야 한다. 즉, 2,3,5 중 하나이므로 이미 7을 시행하기 전 단계에서 체에 걸러졌다는 것이다.

즉 1~n까지 수에서 소수를 찾을게 된다면,
sqrt(n)보다 작은 소수값까지에서 소수가 아닌 수들이 다 체에 걸러지게 된다.
그렇다면 소수 7까지로 체에 거릴 수 있는 n의 수는 120이다. 그리고
11까지로 체에 거를 수 있는 n의 수는 12의 제곱인 144 전까지인 143인 셈이다.

에라토스테네스의 체 의 방법의 시간 복잡도는 O(nloglogn)이고 첫번째 방법은 O(n**2)으로 시간초과이다.
에라토스테네스의 체의 방법으로 푸는 것이 훨씬 효율적이다.

문제 2.

입력된 수의 제곱근을 구하는 함수를 작성해보자. (math.sqrt 를 사용하지 않고)

• 오차범위는 소수점 3자리 까지로 제한한다.

def solution(x)
	x = int(input())
	a= x**0.5
print(round(a,3))

-> pow 사용하는 거와 같다.

pow(number,0.5)
-> number**0.5

문제 3.
{}. (), [] 의 괄호가 문자열로 주어졌을 때 이 문자열이 아래의 조건에 맞는지 출력하는 코드를 작성해보자.

• 각 괄호는 같은 형식의 괄호와 쌍이 된다.
• 누적된 괄호는 각 쌍에 맞추어 닫힐 수 있다.

작동 예시
Input: "()[]{}"
Output: true

Input: "(]"
Output: false

Input: "([)]"
Output: false

Input: "{[]}"
Output: true

def is_valid(s):
  a={'(':0, ')':1, '[':2, ']':3, '{':4, '}':5}
  length = len(s)
  if length % 2 != 0:
    return False
  
  r =[s[0]]
  for i in range(1,length):
    if len(r)>0:
      if a[r[len(r)-1]]+1 == a[s[i]]:
        r.pop()
      else:
        r.append(s[i])
    else:
      r.append(s[i])
  
  if len(r) ==0:
    return True
  return False

다른 풀이 방법

def is_valid(string):
	left = ['(', '{', '[']
	right = [')', '}', ']']
	stack = []
	for letter in string:
		if letter in left:
			stack.append(letter)
		elif letter in right:
			if len(stack) <= 0:
				return False
			if left.index(stack.pop()) != right.index(letter):
				return False
	return len(stack) == 0
   ```