Queue 개념 이해하기
큐의 구조는 스택과 다르게
'선입선출',FIFO(First In First Out)의 구조를 가지고 있다. 스택은 막힌 박스와 같아 먼저 들어온 것이 가장 나중에 나가는 구조지만, 큐는 먼저 들어온 것이 먼저 나가는 구조이다. 그래서 데이터를 추가한 순서대로 제거할 수 있기 때문에 스트리밍(streaming), 너비 우선 탐색(breath first search) 등 소프트웨어 개발에서 널리 응용되고 있다.
좋은 예로 은행에 있는 번호표가 있다. 은행에 방문하여 기다리는데 나보다 늦게 온 다른 분이 먼저 업무를 본다면 기분이 나쁘지 않겠는가?
이러한 상황을 만들지 않기 위해 은행에서는 번호표를 나눠준다. 먼저 온 손님은 늦게 온 손님보다 먼저 서비스를 받게 하기 위해서이다. 이러한 은행의 번호표의 체계가 큐(Queue)이다.
은행의 번호표를 다시 한번 생각해보면,
현재 내가 303번의 번호표를 뽑았다고 가정해보자.
지금 302번까지 서비스를 받은 상태이다. 그러면 번호표 시스템 내부에서는 다음 서비스를 받을 번호를 어떻게 기억을 할까?
1번부터 확인하면서 이 손님이 서비스를 받았는지 안받았는지 확인을 하며 다음으로 호출할 번호를 정할까? 그러면 너무 비효율적일 것이다.
서비스를 받을 처음 위치와 마지막의 위치만 기억하면 모든게 쉽게 풀린다.
이 위피들을 큐(Queue)에서는 front, rear이라고 한다.
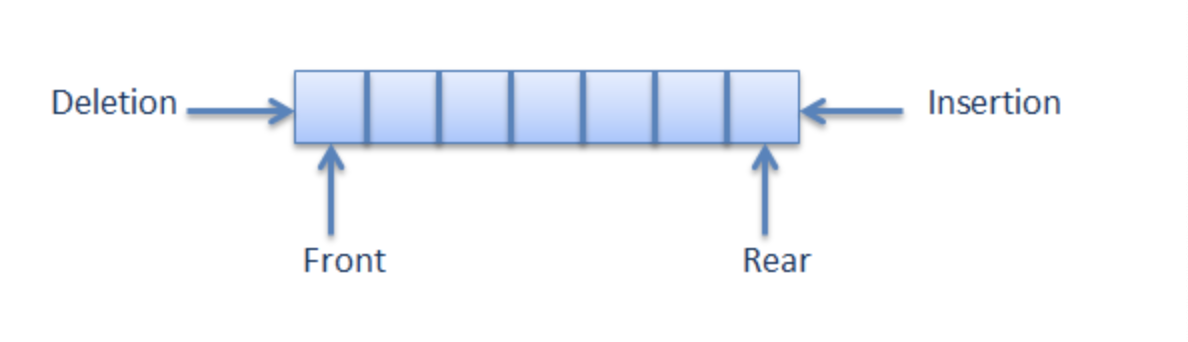
위 그림을 보면 Deletion, Insertion이라는 용어가 있다. 이 용어보다는 많은 사람들이 Dequeue, Enqueue라는 용어를 사용한다. Enqueue는 위 그림에서 Insertion과 같다. 마지막으로 온 손님에게 번호표를 주는 것이다. 그럼 Dequeue는 서비스를 받은 번호표는 대기목록에서 지우는 것이라고 할 수 있다. 그래야 다음으로 호출할 번호를 알 수가 있으니까.
정리하면,
(1) Enqueue : 큐 맨 뒤에 어떠한 요소를 추가, 마지막으로 온 손님에게 번호표 발부
(2) Dequeue : 큐 맨 앞쪽의 요소를 삭제, 창구에서 서비스를 받은 손님의 번호표를 대기목록에서 삭제
(3) Peek : front에 위치한 데이터를 읽음, 다음 서비스를 받을 손님이 누구인지 확인
(4) front : 큐의 맨 앞의 위치(인덱스), 다음 서비스를 받을 손님의 번호
(5) rear : 큐의 맨 뒤의 위치(인덱스), 마지막에 온 손님의 번호
(6) isFull : 큐가 꽉 찼는지 확인. rear = n-1 즉 rear가 마지막 인덱스이면 꽉 찬것 (선형 큐)
(7) isEmpty : 큐가 비었는지 확인. front = rear 이면 큐가 비었다고 판단 (선형 큐)
queue의 종류는?
1. Linear Queue(선형 큐)
- 기본적인 큐의 형태
- 막대 모양으로 된 큐로, 크기가 제한되어 있고 빈 공간을 사용하려면 모든 자료를 꺼내거나 자료를 한칸 씩 옮겨야 한다는 단점이 있다.
Enqueue
1번이 Enqueue 되어진 상태이다. 첫 번째로 번호표를 뽑은 사람이므로 front와 rear이 둘다 1번을 가르키고 있다.
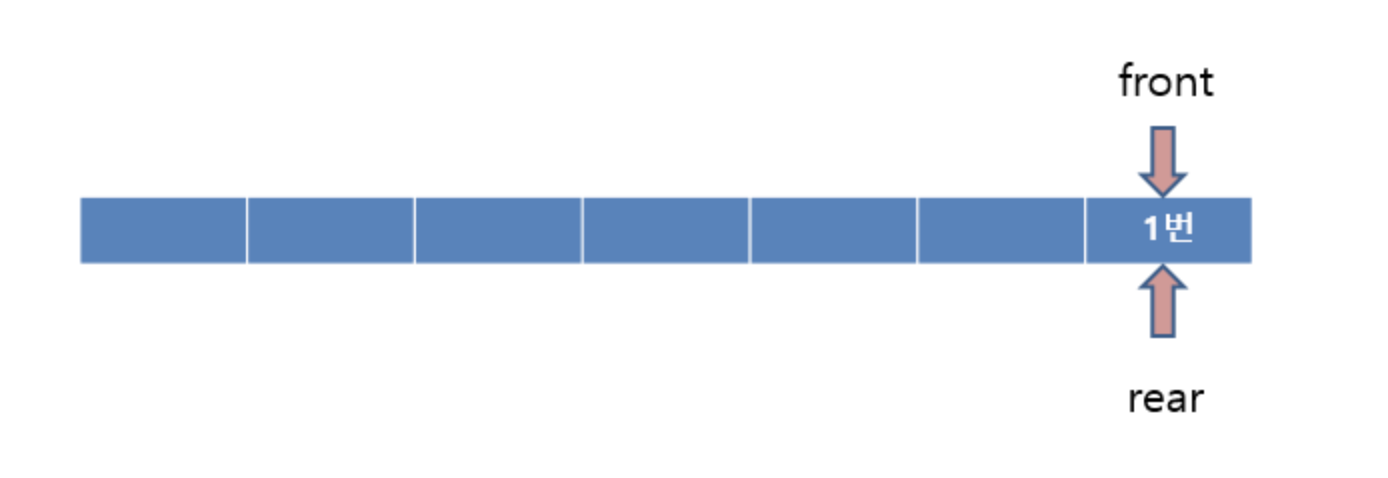
다음으로 2,3,4번이 Enqueue 기능을 수행 한 상태이다. Front는 고정되어 있고 rear만 가장 나중에 들어온 4번을 가르키고 있는 상태이다.
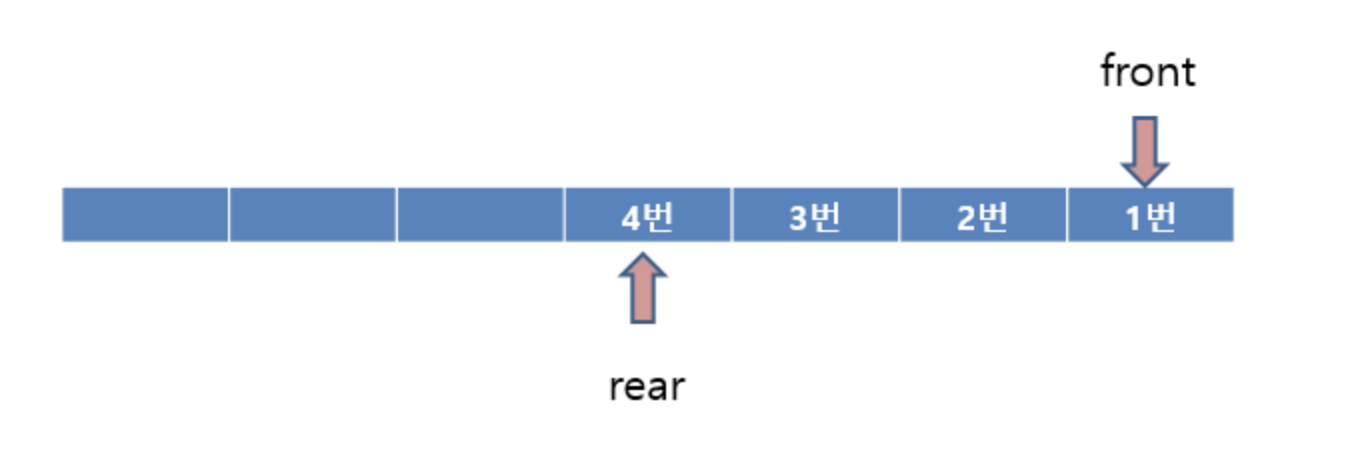
Dequeue
다음으로 Dequeue 기능이다. Dequeue는 반대로 큐에서 데이터를 내보내는 기능을 수행한다.
Dequeue 기능을 수행하고 front의 인덱스를 증가시키는게 보통이지만 여기서는 front를 고정시키고 rear 인덱스만 줄인 채로 뒤에 데이터를 앞으로 이동시키는 방식을 사용한다.
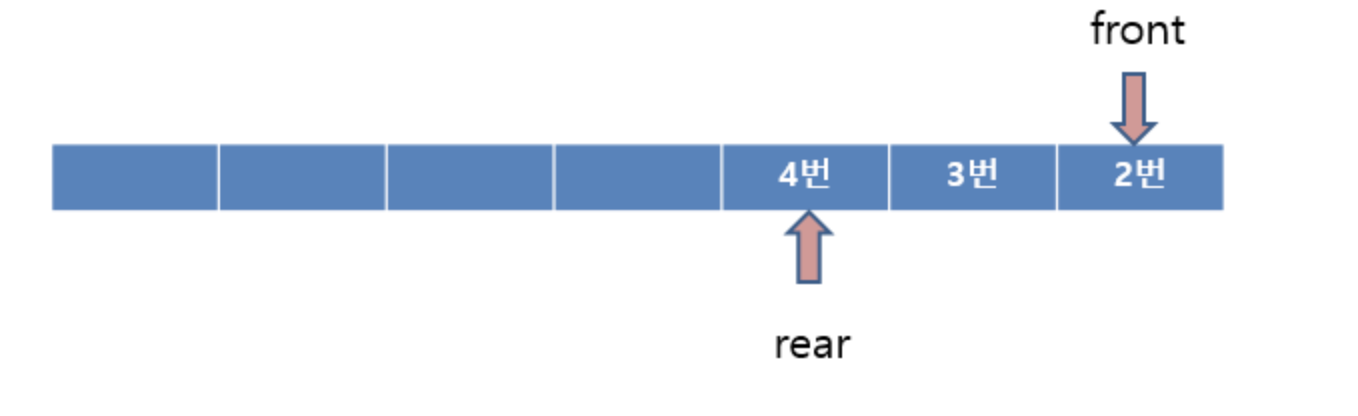
Dequeue를 두번 수행하고 나면 1번과 2번이 순차적으로 큐에서 내보내지고 front는 고정된채로 뒤에 데이터가 앞으로 한칸씩 이동하게 된다. 이 방식은 나중에 rear이 큐의 마지막 인덱스를 가르키고 있을 때 앞의 공간을 활용하기 위해서이다.
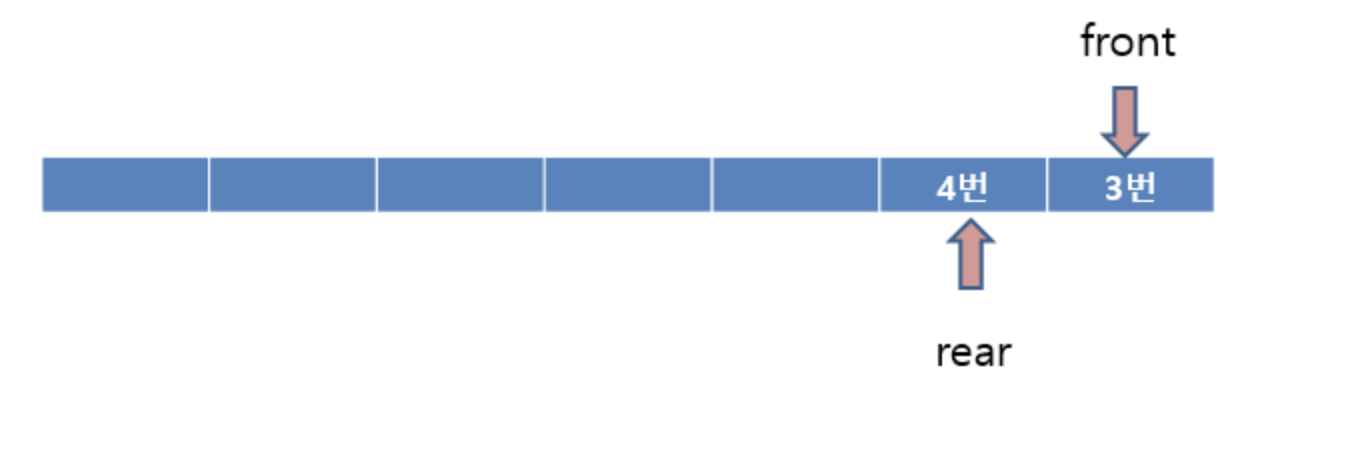
선형 큐의 문제점
일반적인 선형 큐는 rear이 마지막 index를 가르키면서 데이터의 삽입이 이루어진다. 문제는 rear이 배열의 마지막 인덱스를 가르키게 되면 앞에 남아있는 (삽입 중간에 Dequeue 되어 비어있는 공간) 공간을 활용 할 수 없게 된다. 이 방식을 해결하기 위해서는 Dequeue를 할때 front를 고정 시킨 채 뒤에 남아있는 데이터를 앞으로 한 칸씩 당기는 수밖에 없다. 그래서 이를 보안하기 위해 나온 것이 원형 큐이다.
2. Circular Queue (원형 큐)
- 선형 큐의 문제점을 보완하고자 나왔다.
- 배열의 마지막 인덱스에서 다음 인덱스로 넘어갈 때
'(index+1) % 배열의 사이즈'를 이용하여Out Of Bounds Exception이 일어나지 않고 인덱스 0으로 순환되는 구조를 가진다.
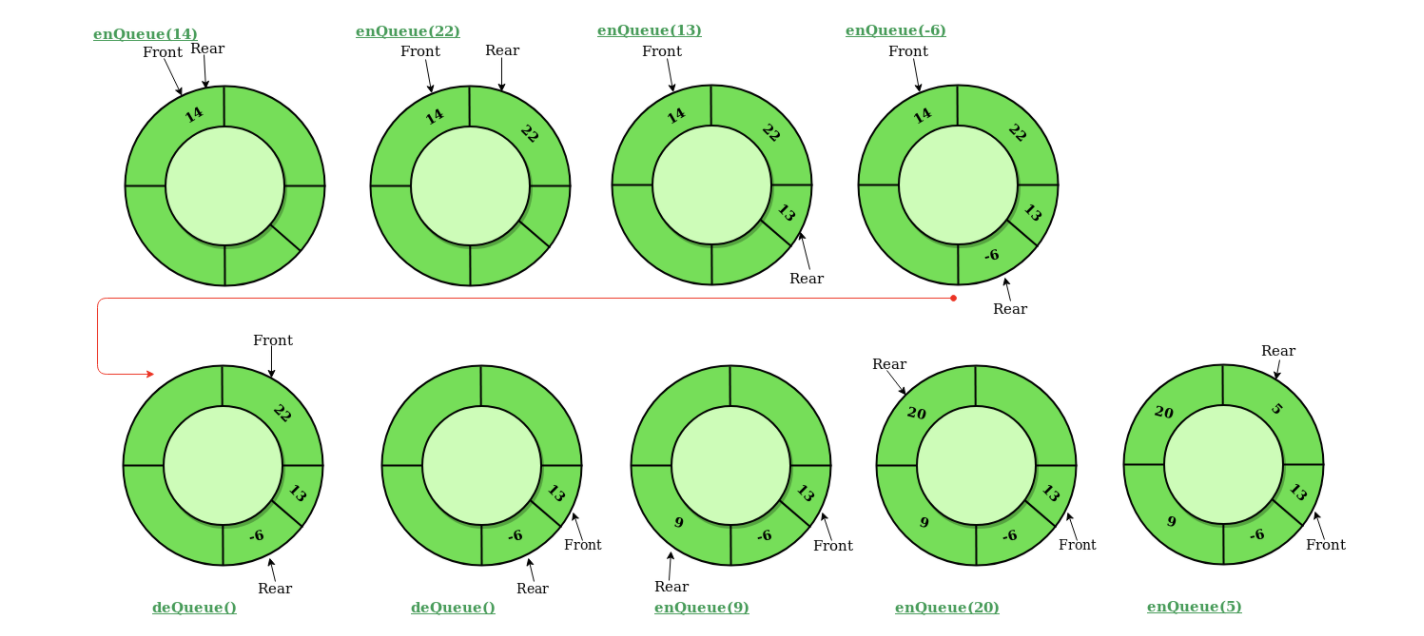
front에 데이터를 넣는 방법과 넣지 않고 비어두는 방법이 있는데 굳이 비어두지 않아도 되므로 데이터의 효율을 위해 나는 원형에 데이터를 다 채울 방법에 대해 알아보려 한다.
초기 front와 rear는 맨 처음 인덱스에 위치한다.
원형에 들어갈 수 있는 데이터 수를 size라고 하면,
Enqueue 연산 시 (데이터 추가) rear = (rear + 1) % size 하여 데이터를 새로 넣는다.
그런데 (rear + 1) % size = front이면 꽉 차 있다고 판단한다.
Dequeue 연산 시 (데이터 삭제) front가 1칸 움직인다. front도 (front+1) % size 만큼 움직인다.**
python으로 circular queue 구현
class CircularQueue():
# constructor
def __init__(self, size): # initializing the class
self.size = size
# initializing queue with none
self.queue = [None for i in range(size)]
self.front = self.rear = -1
def enqueue(self, data):
# condition if queue is full
if ((self.rear + 1) % self.size == self.front):
print(" Queue is Full\n")
# condition for empty queue
elif (self.front == -1):
self.front = 0
self.rear = 0
self.queue[self.rear] = data
else:
# next position of rear
self.rear = (self.rear + 1) % self.size
self.queue[self.rear] = data
def dequeue(self):
if (self.front == -1): # codition for empty queue
print ("Queue is Empty\n")
# condition for only one element
elif (self.front == self.rear):
temp=self.queue[self.front]
self.front = -1
self.rear = -1
return temp
else:
temp = self.queue[self.front]
self.front = (self.front + 1) % self.size
return temp
def display(self):
# condition for empty queue
if(self.front == -1):
print ("Queue is Empty")
elif (self.rear >= self.front):
print("Elements in the circular queue are:",
end = " ")
for i in range(self.front, self.rear + 1):
print(self.queue[i], end = " ")
print ()
else:
print ("Elements in Circular Queue are:",
end = " ")
for i in range(self.front, self.size):
print(self.queue[i], end = " ")
for i in range(0, self.rear + 1):
print(self.queue[i], end = " ")
print ()
if ((self.rear + 1) % self.size == self.front):
print("Queue is Full")
3. Priority Queue(우선순위 큐)
- 우선순위 큐(Priority Queue)는 들어가는 순서에 관계없이 큐에서 dequque 될 때, 우선순위에 맞게 나간다.
- 예를들어 A,B,C가 있을 때, A가 우선순위가 1, B가 3, C가 2면 C, B, A순으로 넣어도 A, C, B순으로 나온다.
- 우선순위 큐의 logarithmic한 성능을 보장하기 위해 항상 이진 트리의 균형을 맞추어야 함
- 완전 이진 트리(Complete Binary Tree)의 구조를 이용하여 트리의 균형을 맞춤
구현방법
- 배열 기반 구현 - 데이터를 삽입 및 삭제하는 과정에서 데이터를 한 칸씩 뒤로 밀거나 한 칸씩 당기는 연산을 수반해야 함 + 원소의 삽입 위치를 찾기 위해 배열의 저장된 모든 데이터와 우선순위의 비교를 진행해야 할 수도 있음
- 연결리스트 기반 구현 - 원소의 삽입 위치를 찾기 위해 첫 번째 노드에서부터 마지막 노드까지에 저장된 데이터들과 우선순위의 비교를 진행해야 할 수도 있음.
- 힙(Heap)을 이용하여 구현 - 모든 부모와 자식 간의 비교만 이루어짐
배열과 연결리스트 기반으로 구현하면 성능이 저하되므로, 일반적으로 힙을 이용하여 많이 구현한다.
힙(Heap)
- 힙은 완전 이진 트리(Complete Binary Tree)이다.
- 모든 노드에 저장된 값(우선순위)들은 자식 노드들의 것보다 (우선순위)가 크거나 같다.
- 직접 연결된 자식-부모 노드 간의 크기만 비교하면 된다.
최대 힙(Max Heap)
최대 힙(Max Heap)은 완전 이진트리이면서, 루트 노드로 올라갈수록 저장된 값이 커지는 구조이다.
우선순위는 값이 큰 순서대로 매기게 된다.
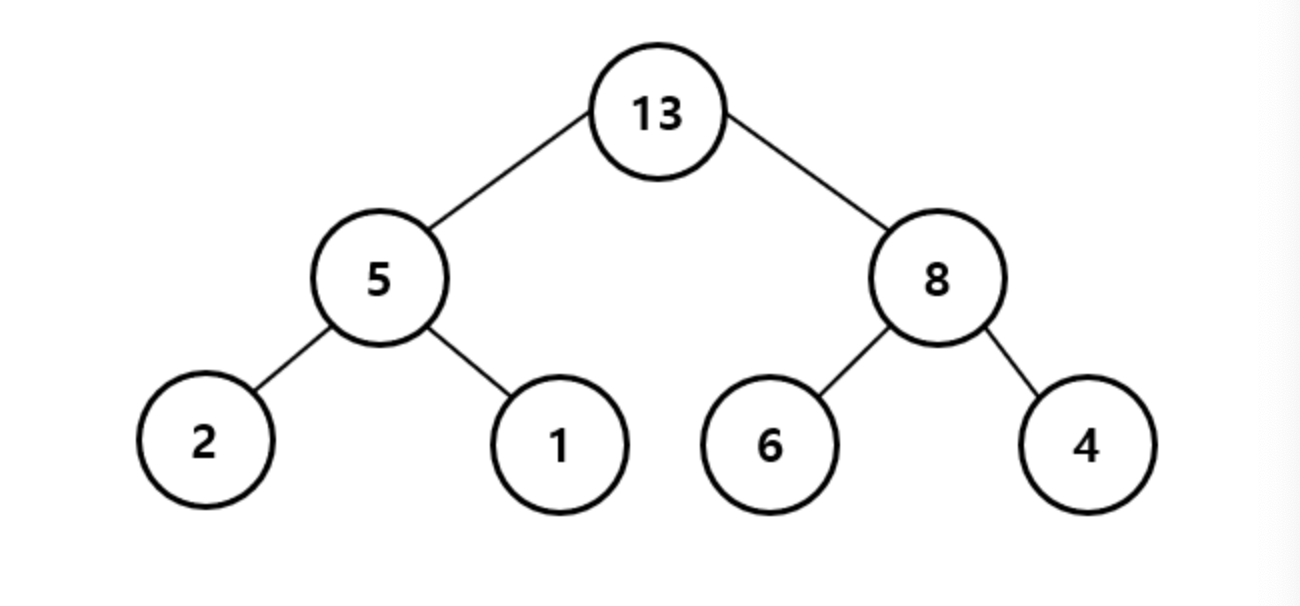
최소 힙(Min Heap)
최소 힙(Min Heap)은 완전 이진트리이면서 루트 노드로 올라갈수록 값이 작아지는 구조이다.
그리고 우선순위는 값이 작은 순서대로 매기게 된다.
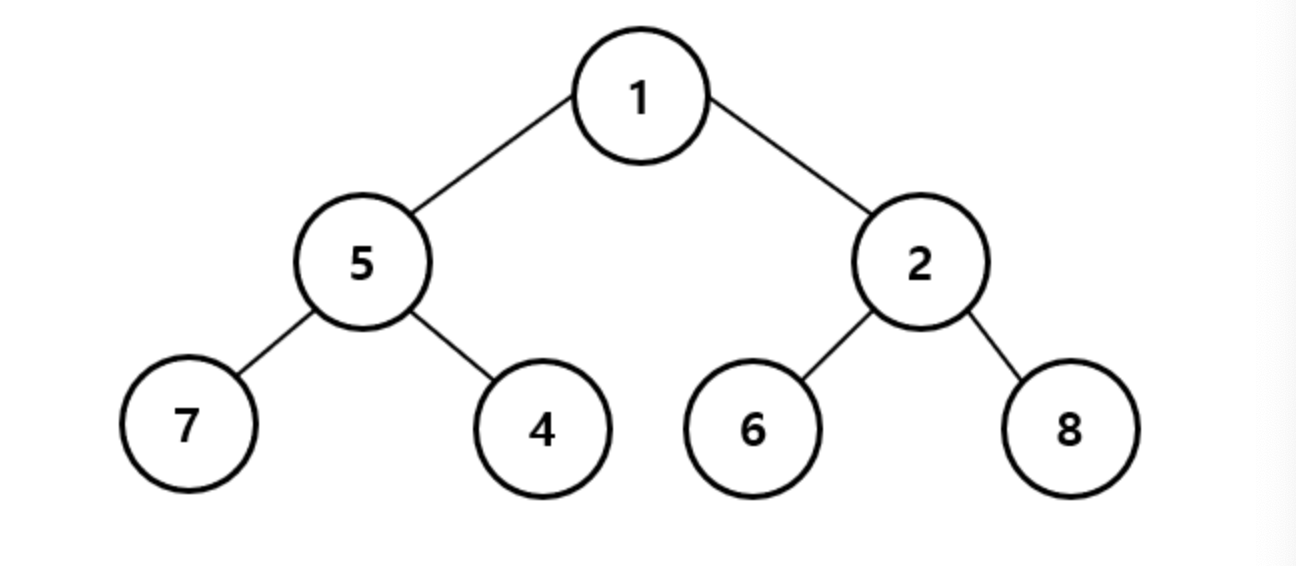
힙에 대한 더 자세한 개념은 다음에 포스팅할 예정이다.
