[청년취업사관학교 새싹]핀테커스 수업 7주차(10/13)

<수업 내용>

Decision Tree

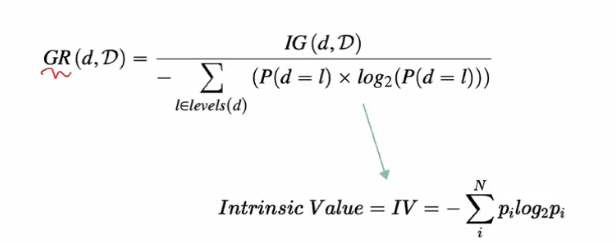
• Information Gain Ratio=Infomation Gain / Intrinsic Value
  

• Intrinsic Value : 분기에 의해 나눠진 타켓 클래스 원소의 개수로 entropy계산

  ** feature에 의해 분기가 너무 세세하게 나워지면, 오히려 잘못된 분기이다. 같은 target class는 최대한 모여 있도록 분기되는 것이 유용하다. 따라서 어떤 feature의 분기에 의한 가지 수를 $N$, $i$번 째 가지에 해당 할 확률을 $p_i$라 하면 intrinsic value는 위의 이미지와 같다

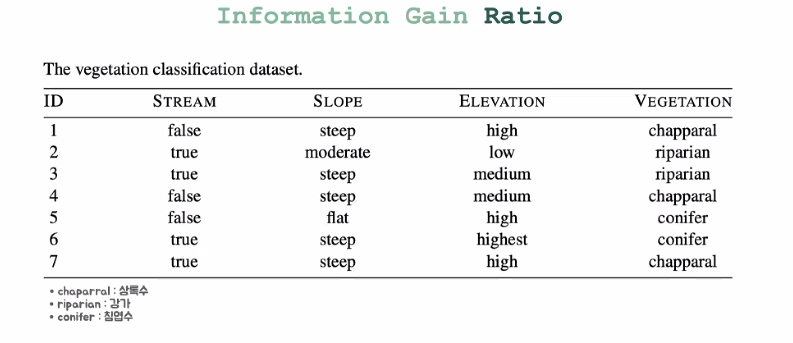
실습

import numpy as np

Total=-((3/7)*np.log2(3/7)+(2/7)*np.log2(2/7)+(2/7)*np.log2(2/7))
stream=(4/7)*(-((2/4)*np.log2(2/4)+(1/2)*np.log2(1/4)))+(3/7)*(-((2/3)*np.log2(2/3)+(1/3)*np.log2(1/3)))
slope=(5/7)*(-((3/5)*np.log2(3/5)+(2/5)*np.log2(1/5)))
elevation=(3/7)*(-(((2/3)*np.log2(2/3))+(1/3)*np.log2(1/3)))+(2/7)*(-(np.log2(1/2)))

IG_stream=Total-stream
IG_slope=Total-slope
IG_elevation=Total-elevation

Iv_stream=-((4/7)*np.log2(4/7)+(3/7)*np.log2(3/7))
Iv_slope=-((5/7)*np.log2(5/7)+(2/7)*np.log2(1/7))
Iv_elevation=-((3/7)*np.log2(3/7)+(2/7)*np.log2(2/7)+(2/7)*np.log2(1/7))

GR_stream=IG_stream/Iv_stream
GR_slope=IG_slope/Iv_slope
GR_elevation=IG_elevation/Iv_elevation

print(GR_stream,GR_slope,GR_elevation)
>>
0.310545833678267 0.5026016408718359 0.47622713750154505


# 첫 번째 분기 feature는 slope

H=-((3/5)*np.log2(3/5)+(1/5)*np.log2(1/5)+(1/5)*np.log2(1/5))
rem_stream=(3/5)*(-np.log2(1/3))
rem_elevation=(2/5)*(-np.log2(1/2))

stream_iv=-((3/5)*np.log2(3/5)+(2/5)*np.log2(2/5))
elevation_iv=-((2/5)*np.log2(2/5)+(2/5)*np.log2(1/5))

stream_gr=(H-rem_stream)/stream_iv
elevation_gr=(H-rem_elevation)/elevation_iv

print(stream_gr,elevation_gr)
>>
0.4325380677663127 0.6661559512003519

# 두번 째 분기 feature는 elevation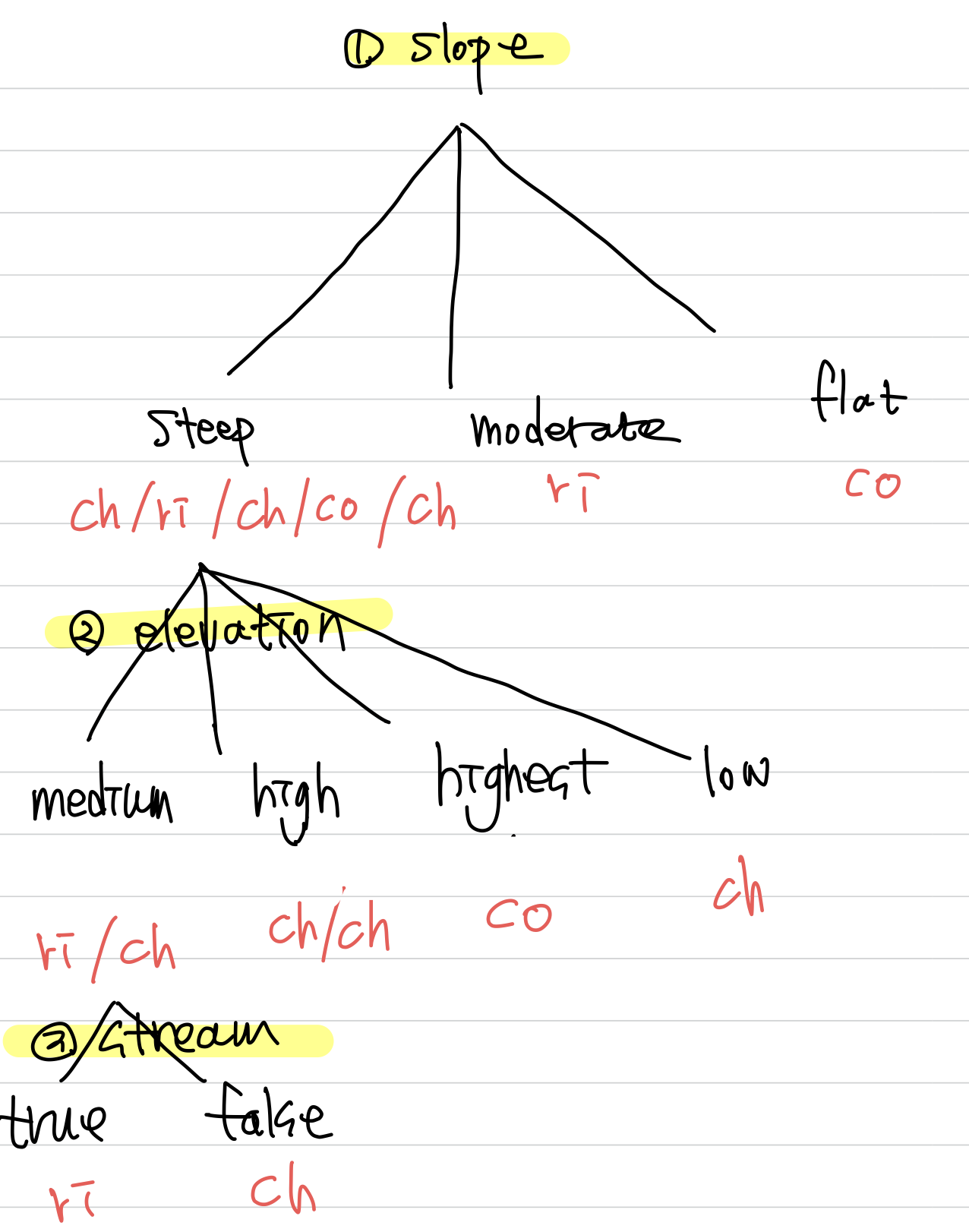

요약

1. target class로 entropy 계산 : $H(t,D)$

2. 각 features에 의한 entropy 계산 : $rem(d,D)=$$\displaystyle\sum$$\left\lvert D_{d=l} \right \rvert\over \left\lvert D \right \rvert$$H(t,D_{d=l})$

3. information gain ,$IG(d,D)=$$H(t,D)-rem(d,D)$

4. instrinsic value , $Iv(d,D)= -p_ilog_{2}p_i$

5. information gaion, $GR=$ $H(t,D)-rem(d,D)\over IG(d,D)$