새해 알고리즘 스터디(1.1~7)
3일차
백준 문제 :
2193, 11726, 11727, 2133
DP 빡공 +2👩💻
DP 공부를 시작하는 마음가짐 🐳
◻️ 내 것이 될 때까지 물어보고 공부하고 정리하자
◻️ 파이써닉한 코드를 많이 보고 연구하자
◻️ 조급해 말고 나만 꽉 채우자
A) 2193번
조건:
- 이친수는 0으로 시작하지 않는다.
- 이친수에서는 1이 두번 연속으로 나타나지 않는다. 즉, 11을 부분 문자열로 갖지 않는다
패턴을 알아보자:
~ 0자리 ➡ 0
~ 1자리 ➡ 1 (1)
~ 2자리 ➡ 1 (10)
~ 3자리 ➡ 2 (100, 101)
~ 4자리 ➡ 3 (1000, 1001, 1010)
dp=[0, 1, 1, 2, 3] 리스트를 먼저 만들 수 있다!
1차 시도(성공):
# append
n =int(input())
dp=[0, 1, 1, 2, 3]
for i in range(5,91):
dp.append(dp[i-1]+dp[i-2])
print(dp[n])N(1 ≤ N ≤ 90)을 적용할 수 있는 for문+range을 작성하고, dp[i-1]+dp[i-2] 패턴을 안에 넣었다.
문제풀이 체크리스트
◻️ 시간 제한 지났음에도 문제 터치 못함
◻️ 시간 제한 후 코드 완성
◻️ 코드 미완성
◻️ 코드 완성 - 에러
◼️ 코드 완성 - 정답
B) 11726번

패턴을 알아보기 위해 [6]까지 그려봤다.
이제 패턴을 알아보자:
~ 1자리 ➡ 1
~ 2자리 ➡ 2
~ 3자리 ➡ 3
~ 4자리 ➡ 5
~ 5자리 ➡ 8
dp=[0, 1, 2, 3, 4, 5] 리스트를 만들고 시작하자!
1차 시도(성공):
memo = {0:0,1:1,2:2}
def num_tile(number : int) -> int:
if number in memo:
return memo[number]
memo[number] = num_tile(number-1) + num_tile(number-2)
return memo[number]
num = int(input())
print(num_tile(num) % 10007)딕셔너리를 활용해 봤다.
** 일반 for i in range():와 시간, 메모리 똑같이 29836KB, 76ms...!
문제풀이 체크리스트
◻️ 시간 제한 지났음에도 문제 터치 못함
◻️ 시간 제한 후 코드 완성
◻️ 코드 미완성
◻️ 코드 완성 - 에러
◼️ 코드 완성 - 정답
C) 11727번
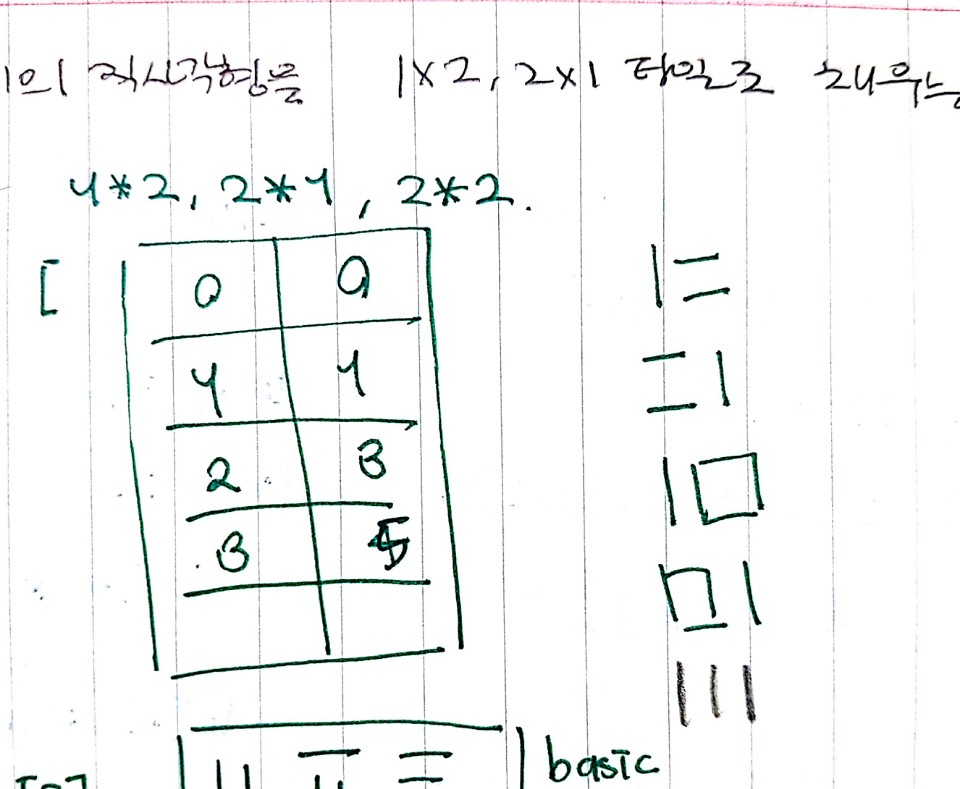
dp=[0, 1, 3, 5]을 만들고, dp[i-1] + (2*dp[i-2])을 패턴으로 잡았다.
1차 시도(성공):
n = int(input())
dp = [0, 1, 3, 5]
for i in range(4,n+1):
dp.append(dp[i-1] + (2*dp[i-2]))
print(dp[n] % 10007)출력 예제인 8을 입력해보고 패턴이 맞는지 확인하기로 했다.171 출력 성공!

문제풀이 체크리스트
◻️ 시간 제한 지났음에도 문제 터치 못함
◼️ 시간 제한 후 코드 완성
◻️ 코드 미완성
◻️ 코드 완성 - 에러
◻️ 코드 완성 - 정답
D) 2133번
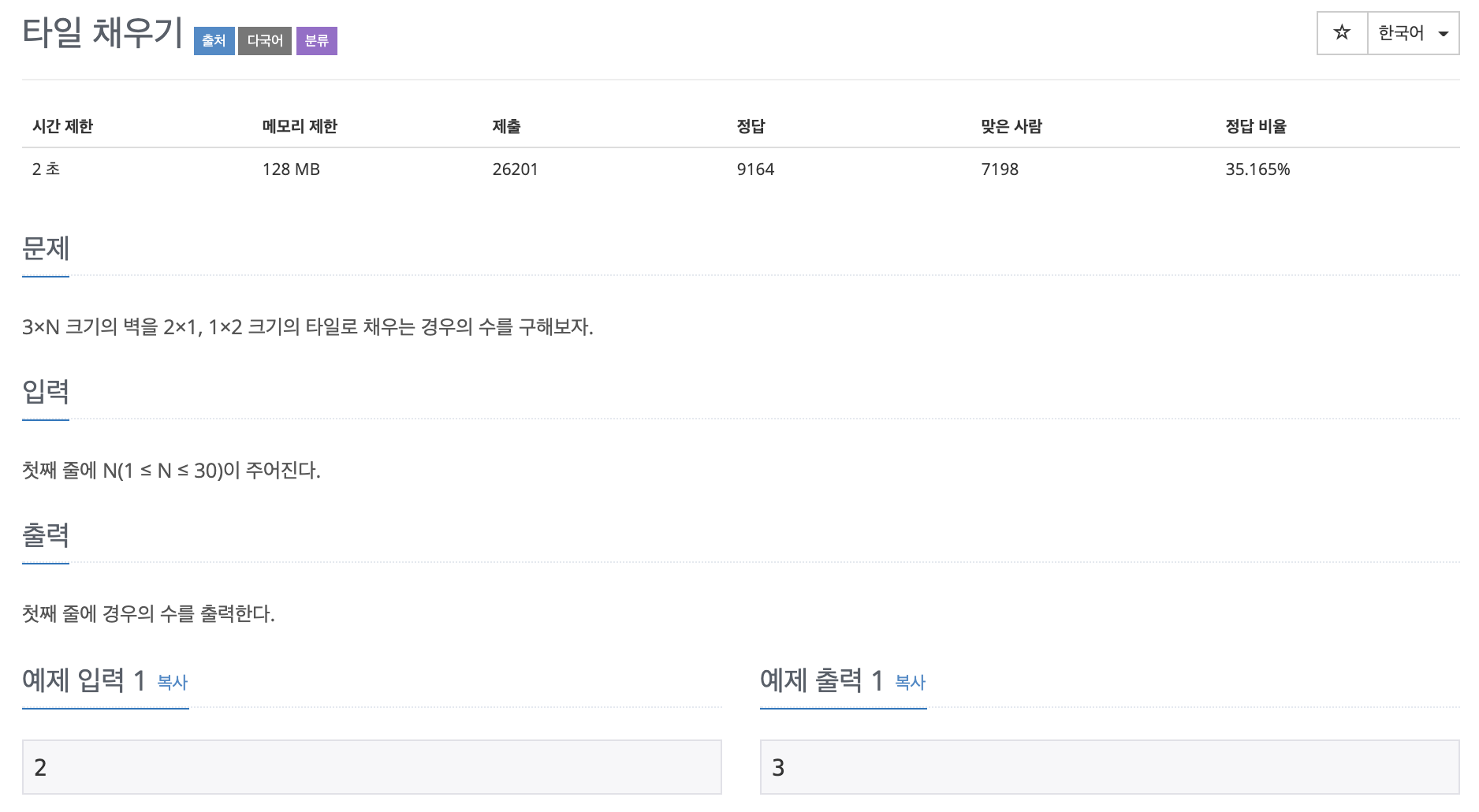
1시간 패턴 찾으려고 그림만 계속 그렸다..

이제 패턴을 알아보자:
~ 1자리 ➡ 0
~ 2자리 ➡ 3
~ 3자리 ➡ 0
~ 4자리 ➡ 11
** 홀수는 무조건 0으로 출력된다
1차 시도(실패):
n = int(input())
dp = [0 for _ in range(31)]
dp[2] = 3
dp[4] = 11
for i in range(6, n+1, 2):
dp.append((dp[i-2] * 3) + 2)
print(dp[n])0이 나왔다✨
소스 코드:
n = int(input())
dp = [0 for i in range(31)]
dp[2] = 3
for i in range(4, 31, 2):
dp[i] = dp[2] * dp[i - 2]
for j in range(4, i, 2):
dp[i] += 2 * dp[i - j]
dp[i] += 2
print(dp[n])출처 - pacific-ocean
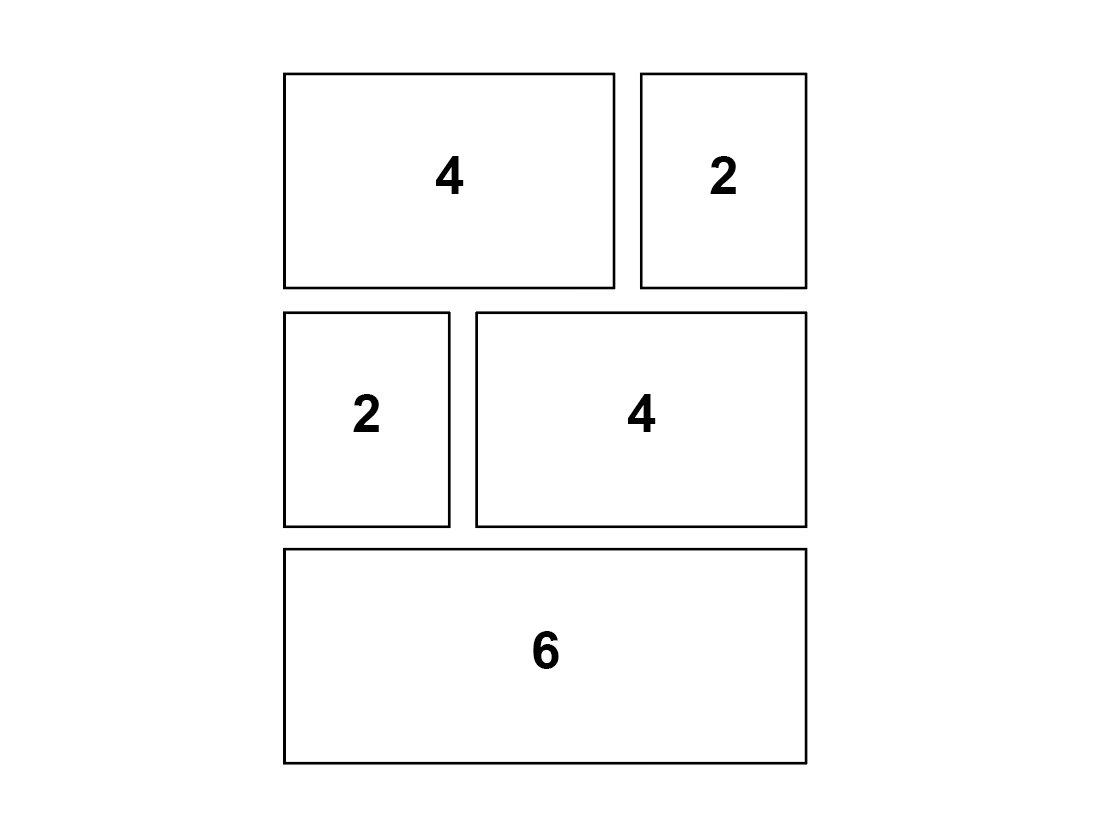
6을 만들 수 있는 방법은 총 3가지다.
- basic[4] + [2]
앞서dp[4]에서 본 모양과dp[2]에서 본 모양 ➡ (11 x 3) * 3 - [2] + new[4]
앞서dp[2]에서 본 모양과 (dp[2]로 만들 수 없는 연결되어 있는 구조를 가진 )dp[4]의 새로운 모양 ➡ 3 * 2 - new[6]
(dp[2], dp[4]로 만들 수 없는 연결되어 있는 구조를 가진)dp[6]의 새로운 모양➡ 2
☄️ dp[6] = 33 + 6 + 2 = 41
1번에 집중한 나머지.. 2번을 잊었다. 이런 실수는 하지말자!
문제풀이 체크리스트
◻️ 시간 제한 지났음에도 문제 터치 못함
◻️ 시간 제한 후 코드 완성
◻️ 코드 미완성
◼️ 코드 완성 - 에러
◻️ 코드 완성 - 정답
Reference
https://www.acmicpc.net/
https://pacific-ocean.tistory.com/208
https://suri78.tistory.com/103

