유클리드 호제법(Euclidean algorithm)

• 2개의 자연수의 최대공약수(GCD, Greatest Common Divisor)를 구하는 알고리즘
• 2개의 자연수 a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다.

알고리즘

1. 큰 수를 작은 수로 나누는 MOD 연산을 수행한다.
2. 앞 단계에서의 작은 수와 MOD 연산 결괏값(나머지)으로 MOD 연산을 수행한다.
3. 단계 2를 반복하다가 나머지가 0이 되는 순간의 작은 수가 최대공약수이다.

그림으로 이해하기

• 270과 192의 최대공약수를 유클리드 호제법으로 찾아보자.

• 위에서 설명한 알고리즘대로 연산을 수행하면 270과 192의 최대 공약수는 6이 된다.

코드 작성하기

• 위에서 설명한 알고리즘을 Python 코드로 작성하면 다음과 같다.

# 최대공약수 구하기
def gcd(a, b):
    # b가 0이면 a가 최대 공약수
    if b == 0:
        return a
    else:
        #  a를 b로 나눈 나머지를 구하여 재귀호출
        return gcd(b, a % b)

a, b = map(int, input().split())  # 두 수 입력, a > b
result = gcd(a, b)

print(result)

• math 모듈의 gcd 함수를 사용하면 최대공약수를 바로 구할 수도 있다.

from math import gcd

a, b = map(int, input().split())  # 두 수 입력
result = gcd(a, b)

print(result)

응용 1 - 최소 공배수 구하기

• 두 수의 최소 공배수(LCM; Least Common Multiple)가 두 수의 곱을 두 수의 최대공약수로 나눈 값임을 이용하면 유클리드 호제법을 이용하여 최소공배수를 구할 수 있다.

# 최대공약수 구하기
def gcd(a, b):
    # b가 0이면 a가 최대 공약수
    if b == 0:
        return a
    else:
        #  a를 b로 나눈 나머지를 구하여 재귀호출
        return gcd(b, a % b)
    
a, b = map(int, input().split())  # 두 수 입력, a > b

lcm = a * b // gcd(a, b)
print(lcm)

• 최대 공약수와 마찬가지로 math 모듈의 gcd 함수를 사용할 수도 있다.

from math import gcd

a, b = map(int, input().split())  # 두 수 입력

lcm = a * b // gcd(a, b)
print(lcm)

• 파이썬 3.9버전에는 최소공배수를 바로 구할 수 있는 lcm 함수도 추가되었다.

from math import lcm

a, b = map(int, input().split())  # 두 수 입력
result = lcm(a, b)

print(result)

응용 2 - 방정식의 해 구하기

알고리즘

해를 구하고자 하는 방정식이 ax + by = c(a, b, c, x, y 는 정수) 와 같을 때 방정식의 해 x, y 를 구하는 알고리즘은 다음과 같다.

1. 유클리드 호제법을 이용하여 나머지가 0이 될 때 까지의 몫, 나머지를 저장한다.
2. 반복으로 구한 나머지와 몫을 이용하여 거꾸로 올라가며 x = y', y = x' - y' * q를 역계산한다.
   ➝ x'는 이전 x, y'는 이전 y를 의미하고 q는 현재 몫을 의미한다.
   ➝ 처음 시작하는 x, y는 이전 값이 없으므로 x', y'를 각각 1, 0으로 지정하여 역계산을 진행한다.
3. 이렇게 재귀 방식으로 알아낸 최종 x, y는 ax + by = gcd(a, b)를 만족한다.
4. c / gcd(a, b) = K를 가정하면 최초 방정식의 해는 Kx, Ky가 된다.
   ➝ 만약 c가 최대공약수의 배수가 아니라면 방정식의 해를 구할 수 없다.

예시를 통해 이해하기

5x + 9y = 2 일 때 만족하는 정수 x, y를 구해보자.

STEP 0

• 조건을 정리하면 다음과 같다.
  

STEP 1

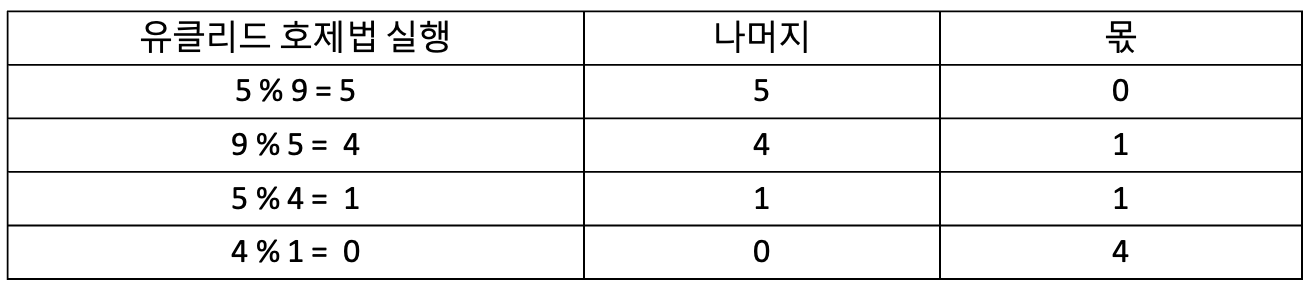
• 유클리드 호제법을 반복 실행하며 몫, 나머지를 저장한다.
• 반복은 나머지가 0이 되면 중단한다.
  

STEP 2

• 반복으로 구한 나머지와 몫을 이용하여 거꾸로 올라가며 x = y', y = x' - y' * q를 역계산한다.
  • x'는 이전 x, y'는 이전 y를 의미하고 q는 현재 몫을 의미한다.
  • 처음 시작하는 x, y는 이전 값이 없으므로 x', y'를 각각 1, 0으로 지정하여 역계산을 진행한다.

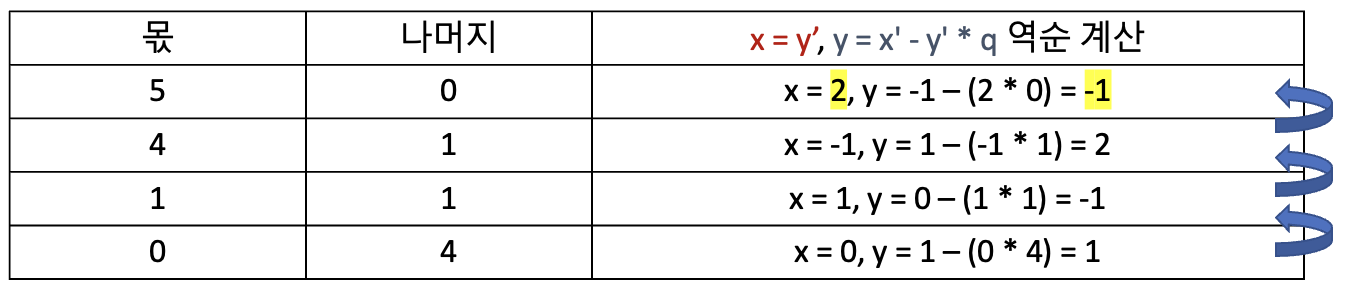
• 이렇게 알아낸 최종 x = 2, y = -1은 ax + by = gcd(a, b)를 만족한다.

STEP 3

• c / gcd(a, b) = K 를 가정하면 최초 방정식의 해를 구할 수 있다.
  • 주어진 조건에서 c = 2, gcd(a, b) = 1 이므로 K = 2 이다.
• 따라서 해 Kx, Ky는 각각 2*2 = 4, 2 * (-1) = -2 가 된다.

코드 작성하기

• 위에서 설명한 알고리즘을 코드로 작성하면 다음과 같다.

a, b, c = map(int, input().split())  # ax + by = c 일 때 세 수 입력

# 유클리드 호제법을 이용한 최대 공약수 구하기
def gcd(a, b):
    if b == 0:
        return a
    else:
        return gcd(b, a % b)

def solve(a, b):
    result = [0] * 2  # x, y를 저장할 배열

    # x', y' 초기 값 설정
    if b == 0:
        result[0] = 1
        result[1] = 0
        return result
    
    q = a // b  # q = a를 b로 나눈 몫
    v = solve(b, a % b)  # 재귀 형태로 유클리드 호제법 수행

    # 역순으로 올라오며 x, y 계산
    result[0] = v[1]
    result[1] = v[0] - v[1] * q
    
    return result

# c가 최대공약수의 배수가 아니라면 방정식의 해를 구할 수 없음
if c % gcd(a, b) != 0:
    print(-1)
else:  # 방정식의 해 구하기
    k = int(c / gcd(a, b))
    ret = solve(a, b)
    x = k * ret[0]
    y = k * ret[1]
    print(x, y)

문제 추천

• BOJ 1850 - 최대공약수
• BOJ 1934 - 최소공배수
• BOJ 1033 - 칵테일
• BOJ 21568 - Ax+By=C