[Algorithm] 최소 공통 조상(Lowest Common Ancestor, LCA) - Python

문지은·2023년 12월 28일

LCA algorithm python tree

Algorithm with Python

목록 보기

15/19

최소 공통 조상(Lowest Common Ancestor, LCA)

두 노드의 공통된 조상 중에서 가장 가까운 조상을 찾는 문제
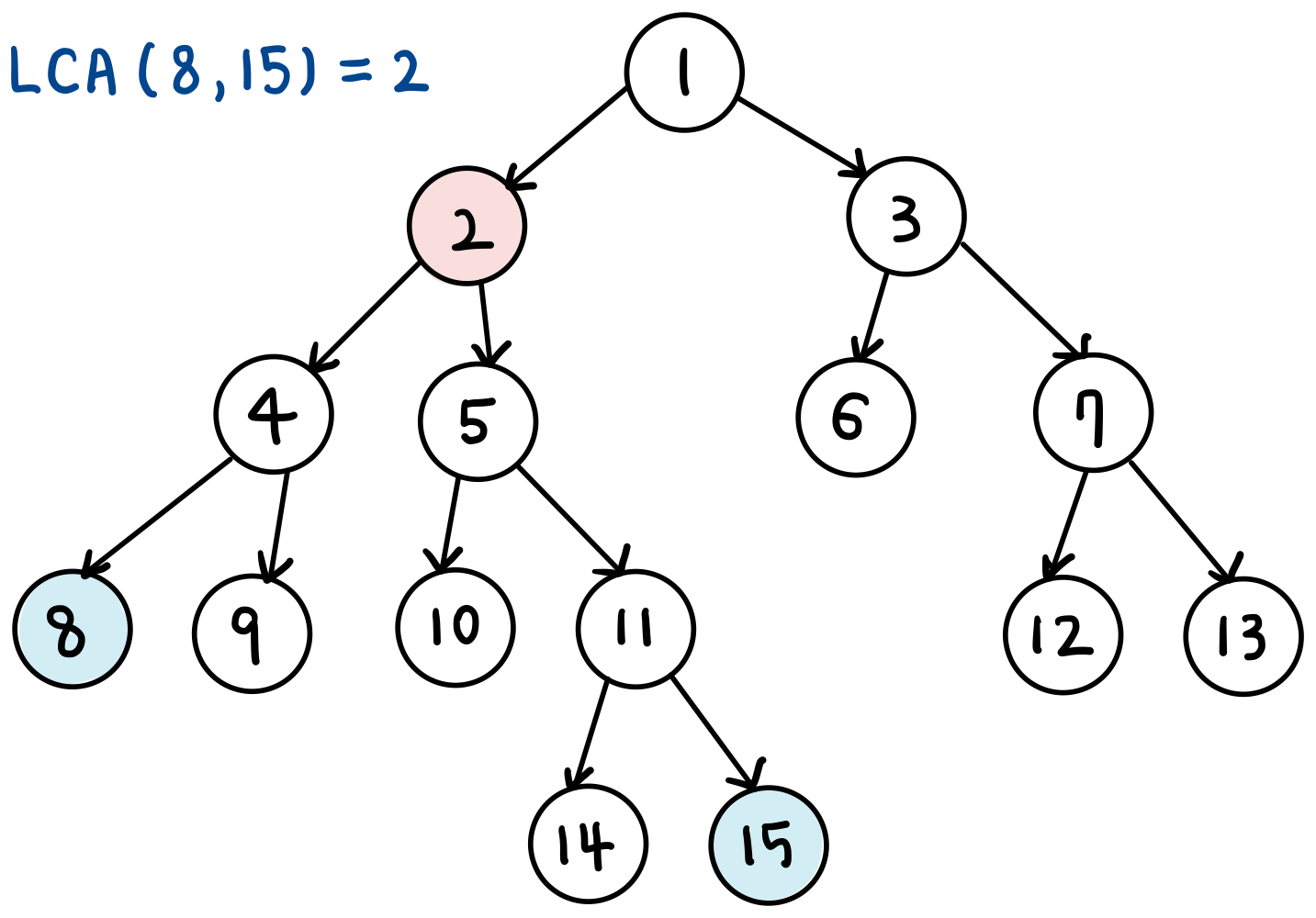
예를 들어, 아래 그림에서 8번 노드와 15번 노드의 공통 조상은 2번 노드
- 8번 노드의 조상 - 1, 2, 4
- 15번 노드의 조상 - 1, 2, 5, 11
- 공통 조상 - 1, 2 중에서 가장 가까운(낮은) 조상은 2번 노드이다.

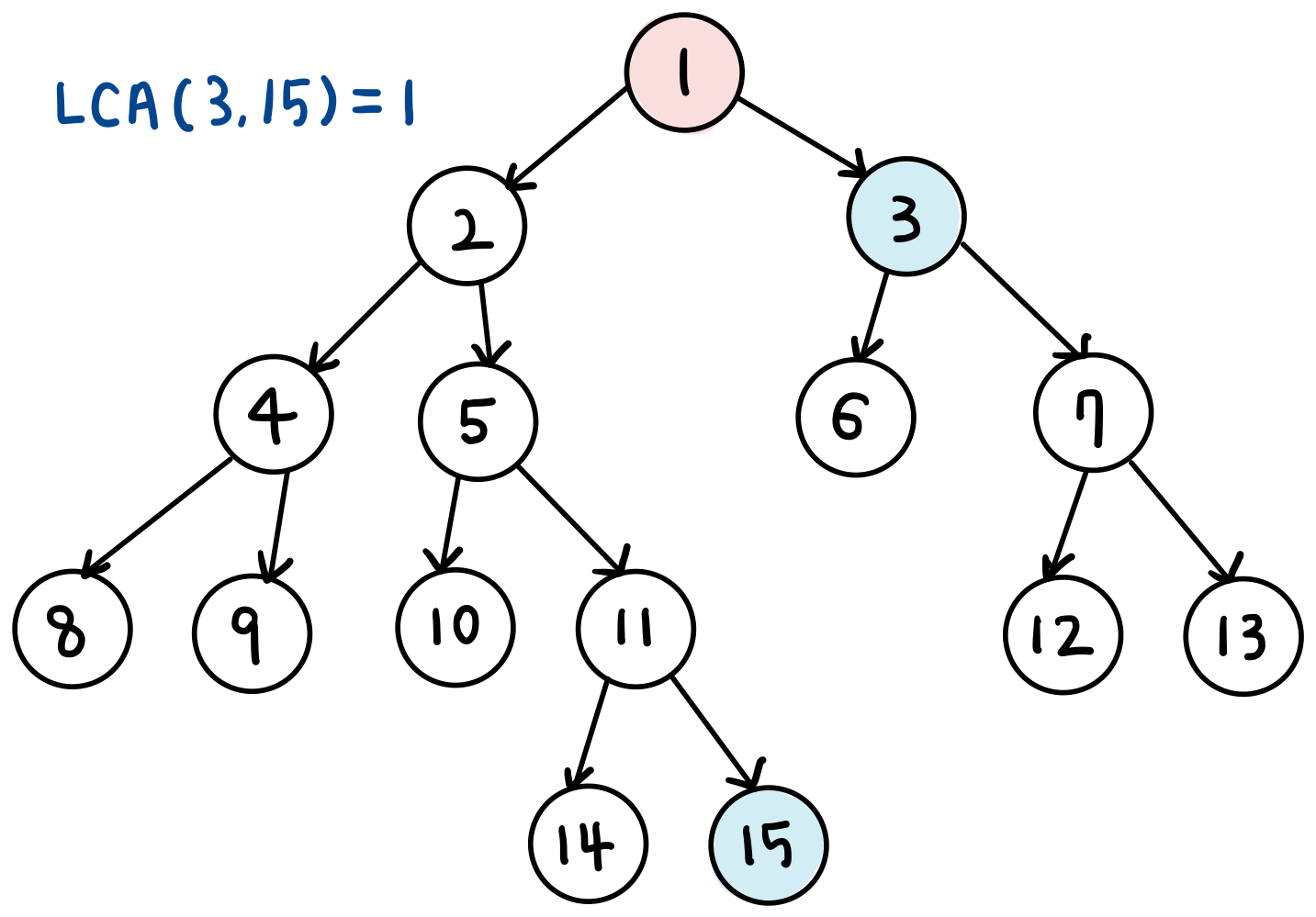
같은 방법으로 3번 노드와 15번 노드의 최소 공통 조상은 1번 노드이다.

기본적인 최소 공통 조상 (LCA) 알고리즘

모든 노드에 대한 깊이(depth)를 계산한다.
최소 공통 조상을 찾을 두 노드를 확인한다.

1) 먼저 두 노드의 깊이(depth)가 동일하도록 거슬로 올라간다.

2) 이후에 부모가 같아질 때까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라간다.
모든 LCA(a,b) 연산에 대하여 2번의 과정을 반복한다.

연산과정 살펴보기

DFS를 이용해 모든 노드에 대하여 깊이(depth)를 계산할 수 있다.

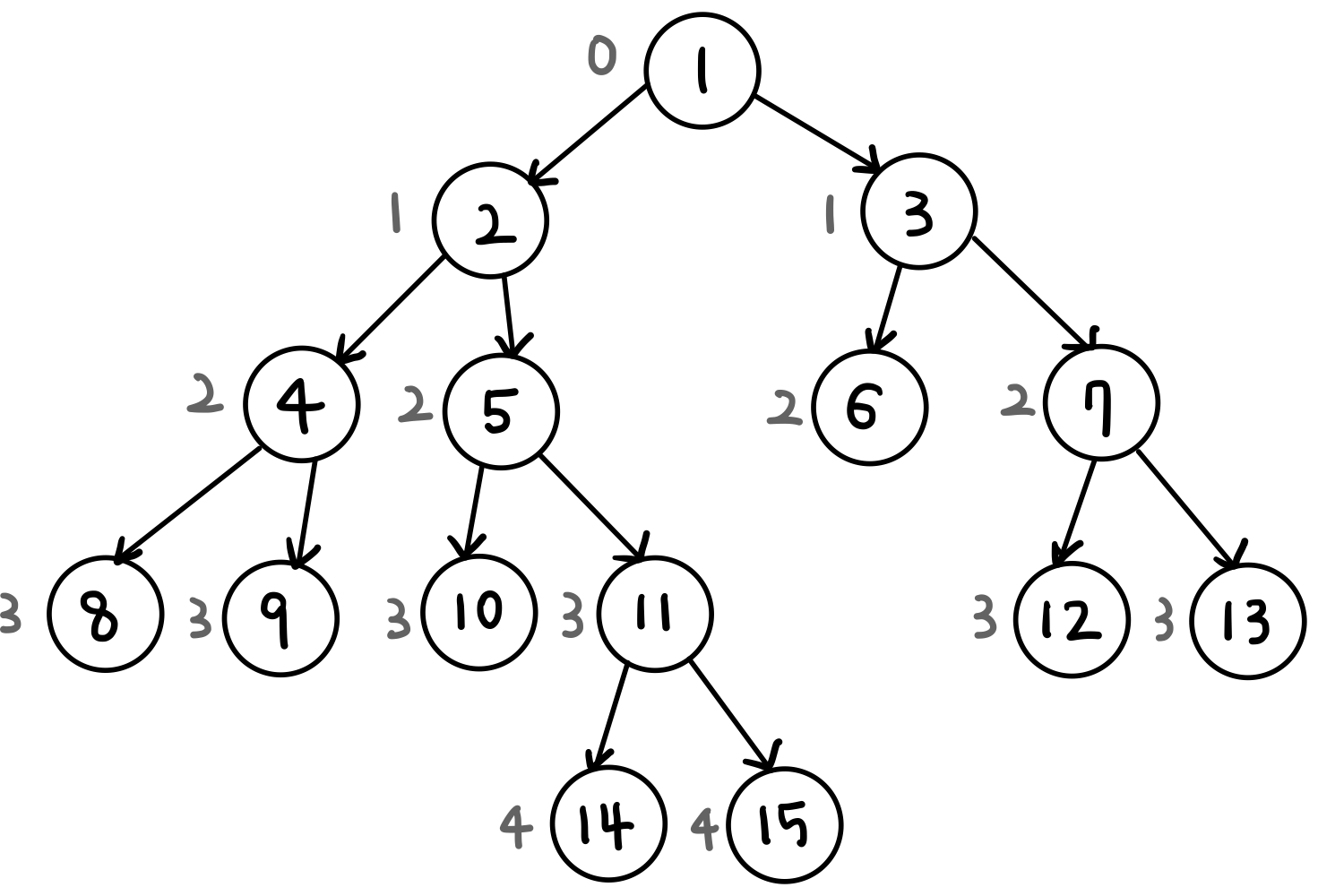
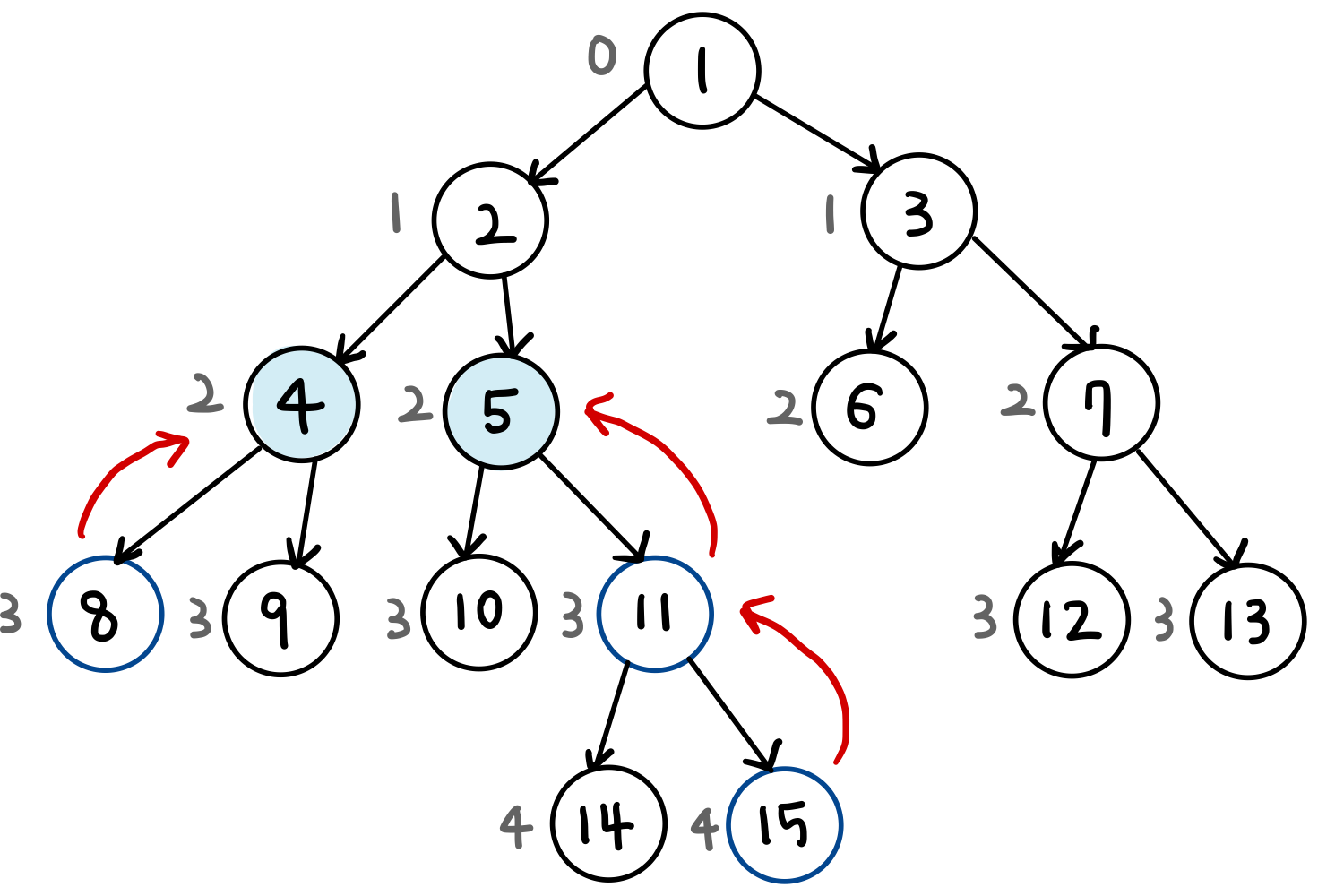
LCA(8번 노드, 15번 노드) 를 구해보자.
먼저 두 노드의 깊이를 맞춘다.

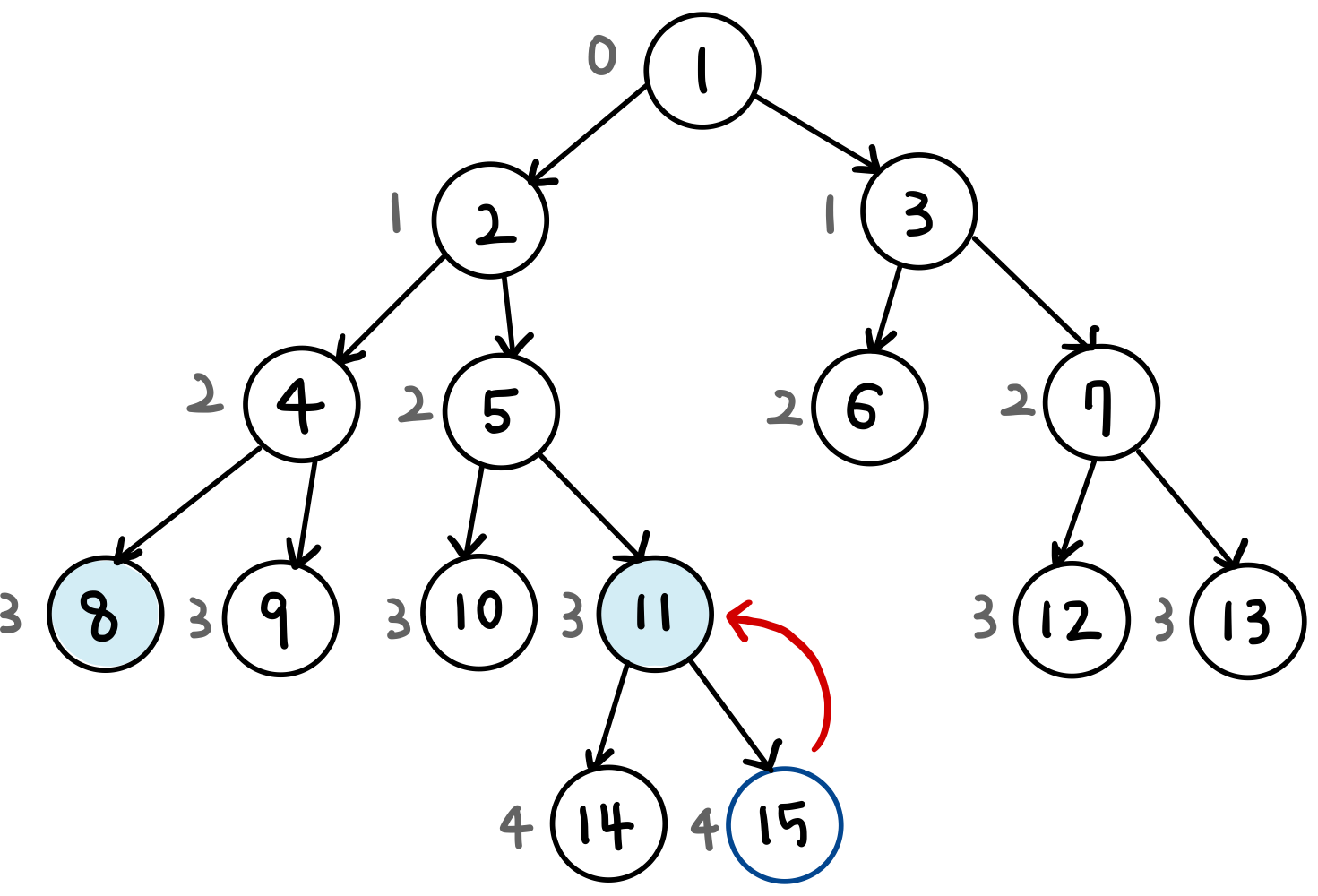
이후에 거슬러 올라간다.

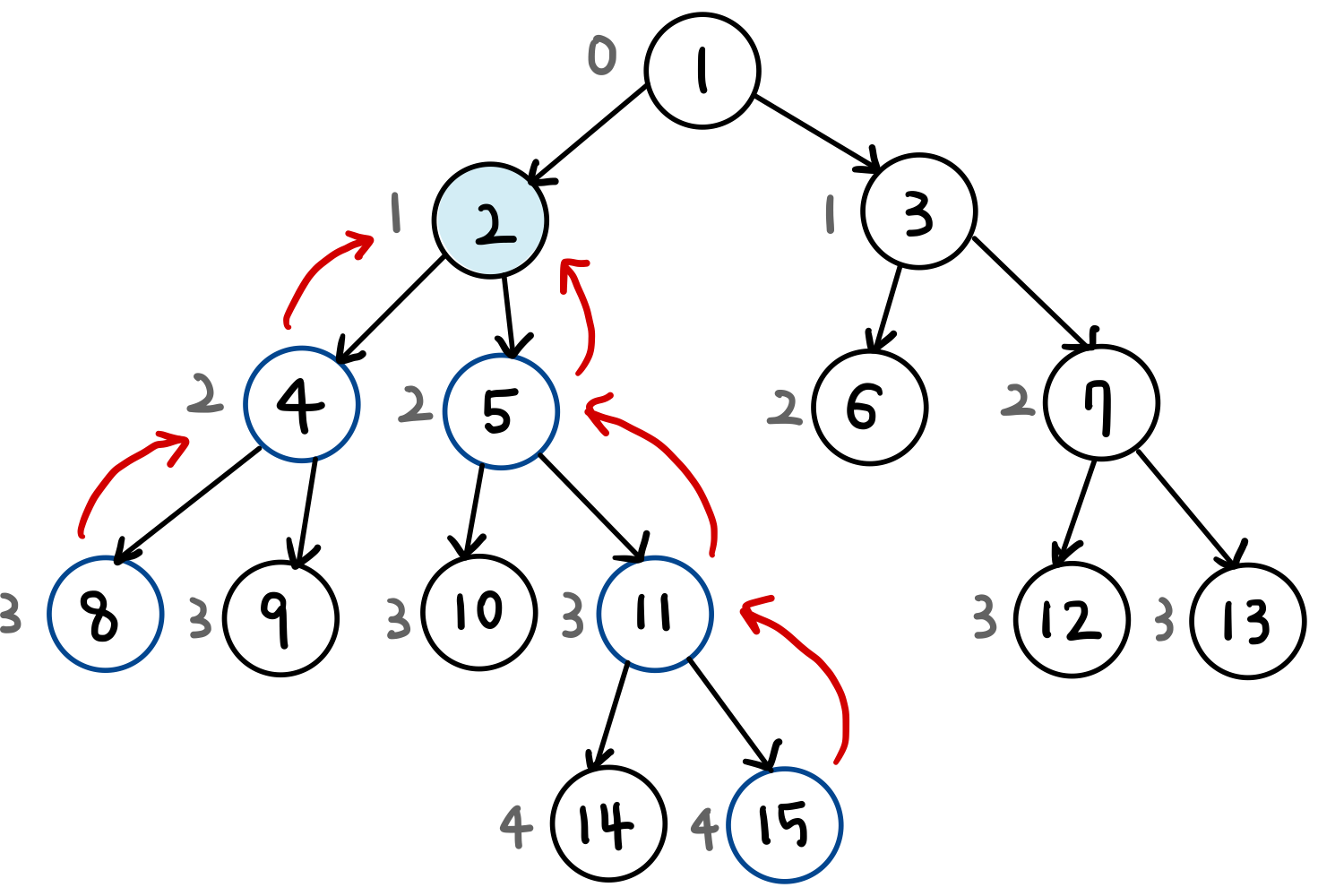
시간 복잡도

매 쿼리마다 부모 방향으로 거슬러 올라가기 위해 최악의 경우 O(N)의 시간 복잡도가 요구된다.
따라서 모든 쿼리를 처리할 때의 시간 복잡도는 O(NM)

알고리즘 구현(Python)

Python 코드로 작성하면 다음과 같다.

import sys
sys.setrecursionlimit(int(1e5)) # 런타임 오류를 피하기
n = int(input())

parent = [0] * (n+1) # 부모 노드 정보
d = [0] * (n+1) # 각 노드까지의 깊이
c = [0] * (n+1) # 각 노드의 깊이가 계산되었는지 여부
graph = [[] for _ in range(n+1)] # 그래프(graph) 정보

for _ in range(n-1):    
	a,b = map(int,input().split())
	graph[a].append(b)
	graph[b].append(a)

# 루트 노드부터 시작하여 깊이(depth)를 구하는 함수
def dfs(x,depth):
    c[x] = True
    d[x] = depth
    for y in graph[x]:
        if c[y]: # 이미 깊이를 구했다면 넘기기
            continue
        parent[y] = x
        dfs(y, depth + 1)
        
# A와 B의 최소 공통 조상을 찾는 함수
def lca(a,b):
    # 먼저 깊이(depth)가 동일하도록
    while d[a] != d[b]:
        if d[a] > d[b]:
            a = parent[a]
        else:
            b = parent[b]
    # 노드가 같아지도록
    while a != b:
        a = parent[a]
        b = parent[b]
    return a

dfs(1,0) # 루트 노드는 1번 노드

m = int(input())

for i in range(m):
    a,b = map(int,input().split())
    print(lca(a,b))

최소 공통 조상 (LCA) 알고리즘 개선하기

각 노드가 거슬러 올라가는 속도를 빠르게 만드는 방법 에 대하여 고민해보자.
만약 총 15칸 거슬러 올라가야 한다면?
- 8칸 → 4칸 → 2칸 → 1칸
2의 제곱 형태로 거슬러 올라가도록 하면 O(logN)의 시간 복잡도를 보장할 수 있다.
메모리를 조금 더 사용하여 각 노드에 대하여 $2^i$ 번째 부모에 대한 정보를 기록해보자.

모든 노드의 깊이와 부모 구하기

모든 노드에 대하여 깊이(depth)와 $2^i$ 번째 부모에 대한 정보를 기록한다.

연산과정 살펴보기

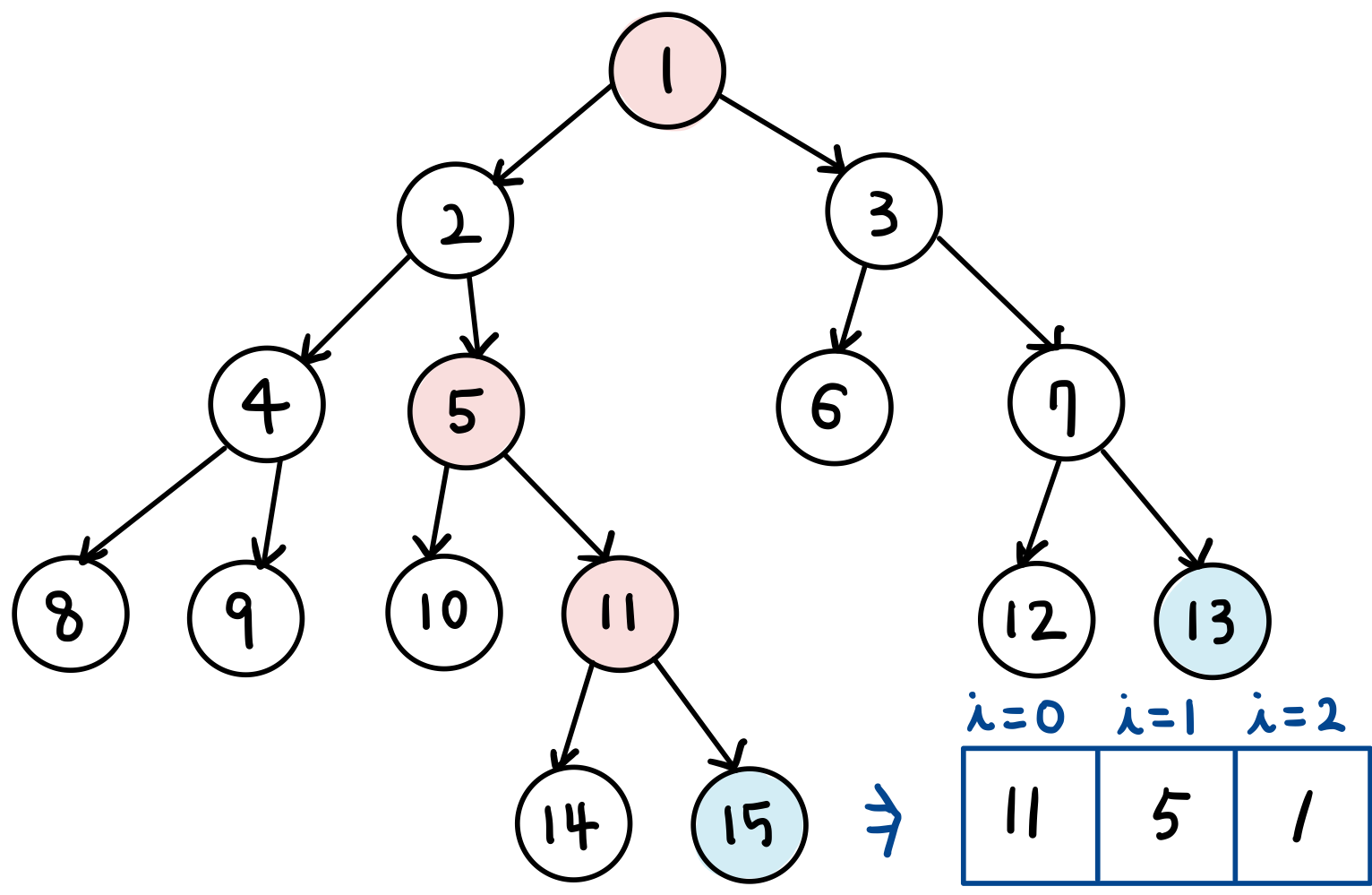
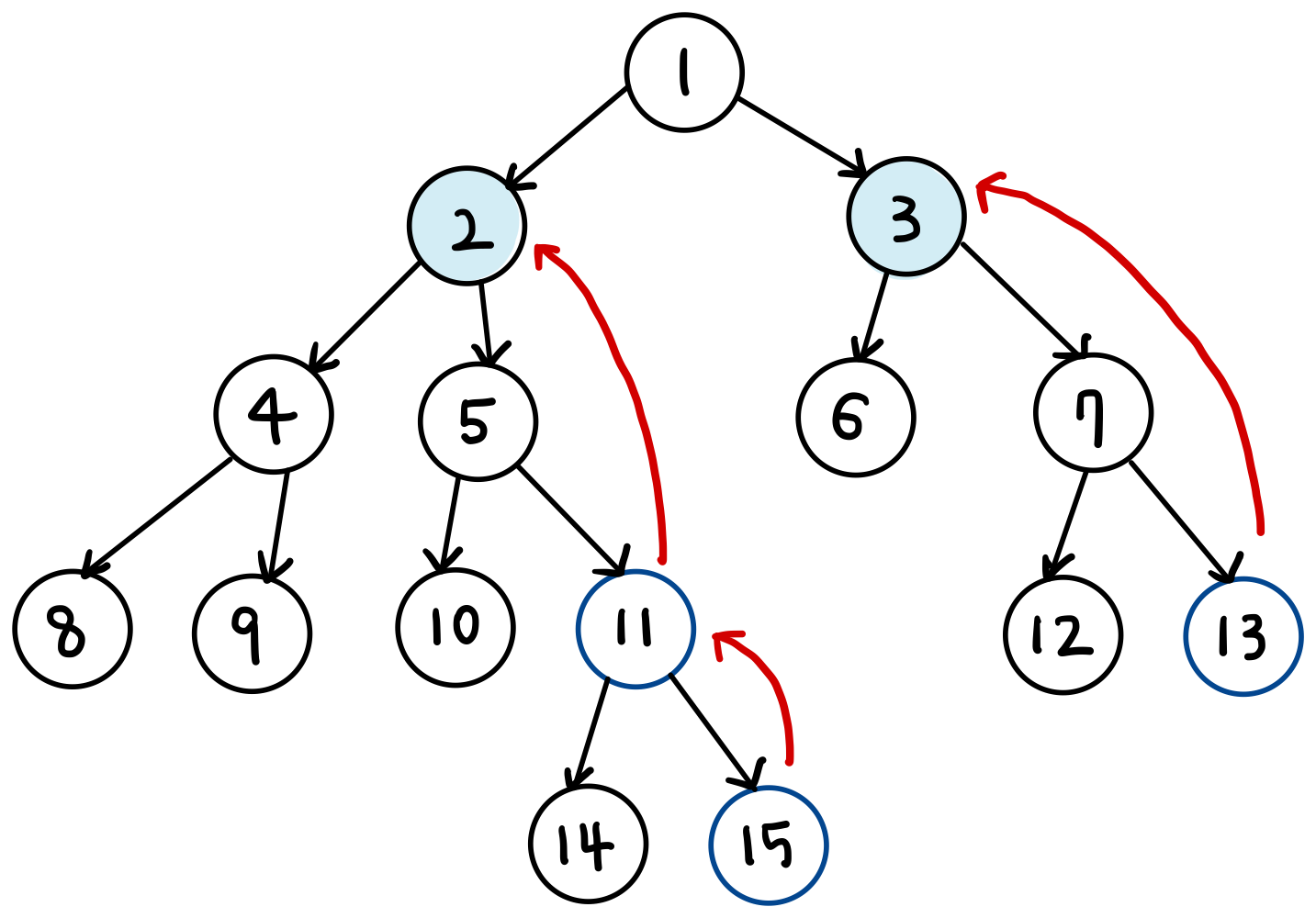
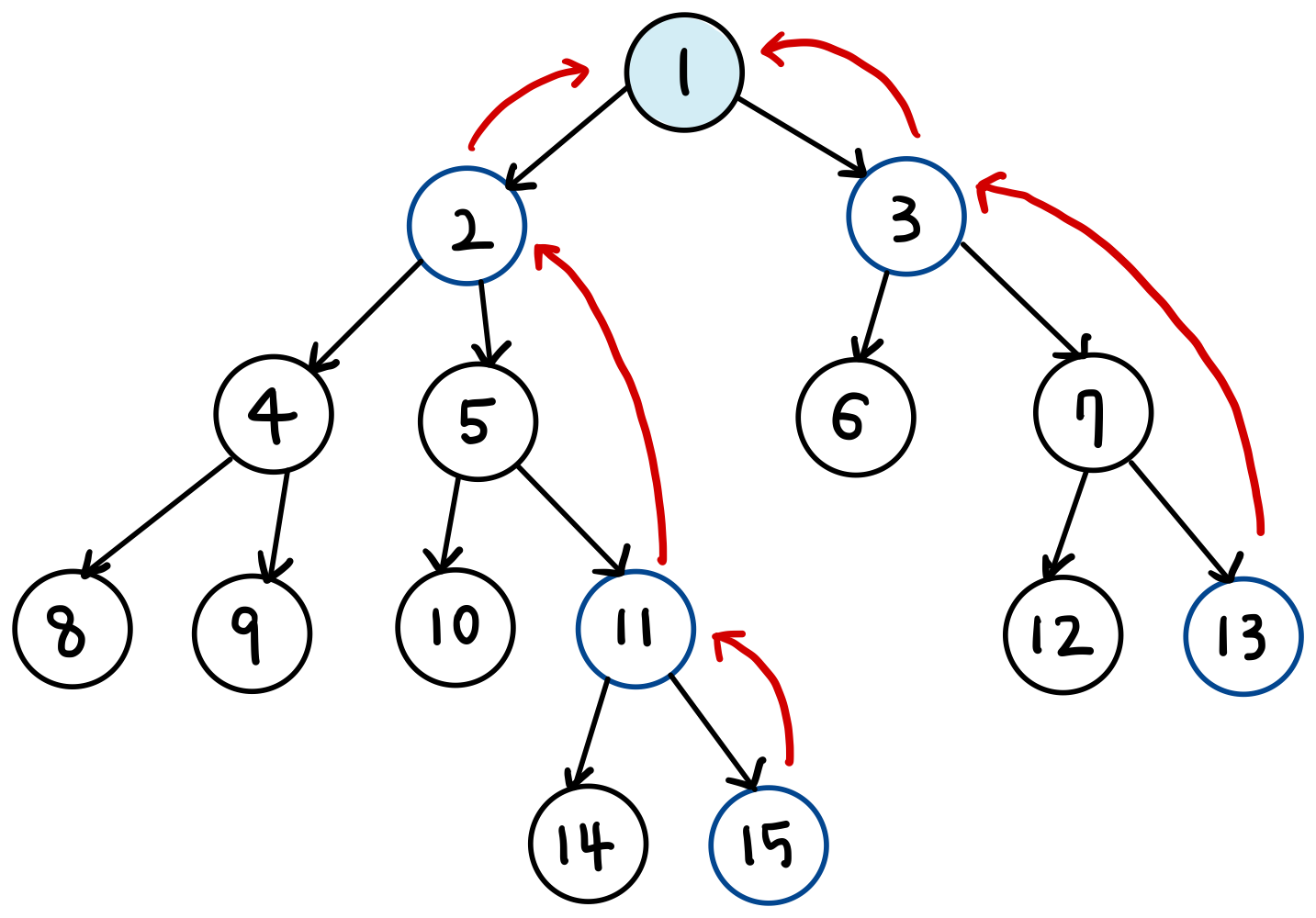
이번에는 13번 노드와 15번 노드의 최소 공통 조상을 구해보자.

먼저 두 노드의 깊이를 맞춘다.

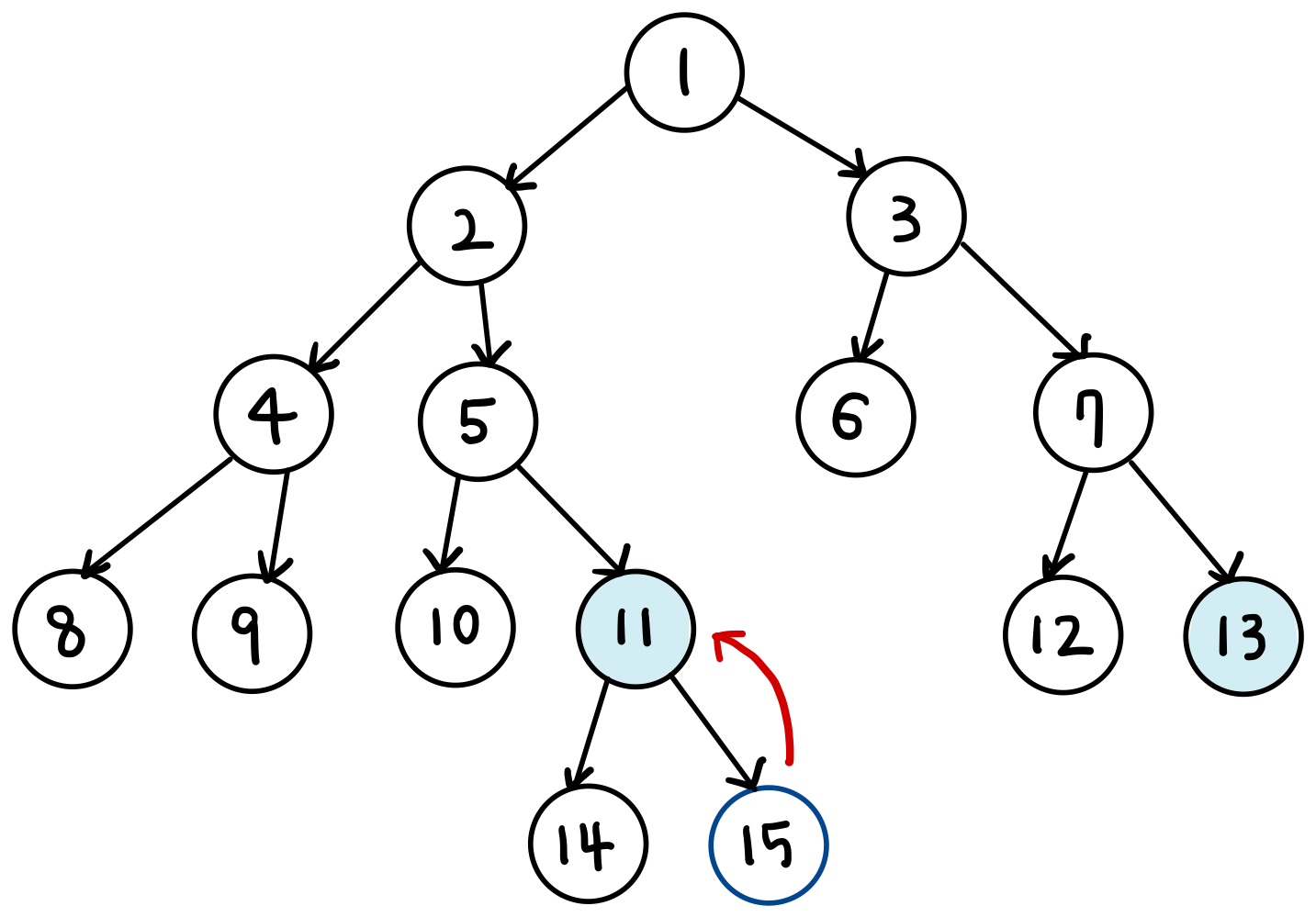
이후에 $2^i$ 씩 거슬러 올라간다.

시간 복잡도 분석

다이나믹 프로그래밍(dynamic programming)을 이용해 시간 복잡도를 개선할 수 있다.
- 세그먼트 트리를 이용하는 방법도 존재한다.
매 쿼리마다 부모를 거슬러 올라가기 위해 O(logN)의 복잡도가 필요
- 따라서 모든 쿼리를 처리할 때의 시간 복잡도는 O(MlogN)

알고리즘 구현(Python)

Python 코드로 작성하면 다음과 같다.

import sys
input = sys.stdin.readline() # 시간 초과를 피하기 위한 빠른 입력 함수
sys.setrecursionlimit(int(1e5)) # 런타임 오류를 피하기 위한 재귀 깊이 제한 설정
LOG = 21 # 2^20 = 1,000,000

n = int(input())
parent = [[0] * LOG for _ in range(n+1)] # 부모 노드 정보
d = [0] * (n+1) # 각 노드까지의 깊이
c = [0] * (n+1) # 각 노드의 깊이가 계산되었는지 여부
graph = [[] for _ in range(n+1)] # 그래프(graph) 정보

for _ in range(n-1):    
	a,b = map(int,input().split())
	graph[a].append(b)
	graph[b].append(a)

# 루트 노드부터 시작하여 깊이(depth)를 구하는 함수
def dfs(x,depth):
    c[x] = True
    d[x] = depth
    for y in graph[x]:
        if c[y]: # 이미 깊이를 구했다면 넘기기
            continue
        parent[y][0] = x
        dfs(y, depth + 1)
        
# 전체 부모 관계를 설정하는 함수
def set_parent():
    dfs(1,0) # 루트 노드는 1번 노드
    for i in range(1,LOG):
        for j in range(1,n+1):
            parent[j][i] = parent[parent[j][i-1]][i-1]

# A와 B의 최소 공통 조상을 찾는 함수
def lca(a,b):
    # b가 더 깊도록 설정
    if d[a] > d[b]:
        a,b= b,a
    # 먼저 깊이(depth)가 동일하도록
    for i in range(LOG-1,-1,-1):
        if d[b] -d[a] >= (1 << i):
            b = parent[b][i]
    # 부모가 같아지도록
    if a==b:
        return a;
    for i in range(LOG-1,-1,-1):
        # 조상을 향해 거슬러 올라가기
        if parent[a][i] != parent[b][i]:
            a = parent[a][i]
            b = parent[b][i]
    # 이후에 부모가 찾고자 하는 조상
    return parent[a][0]

set_parent()

m = int(input())

for i in range(m):
    a,b = map(int,input().split())
    print(lca(a,b))