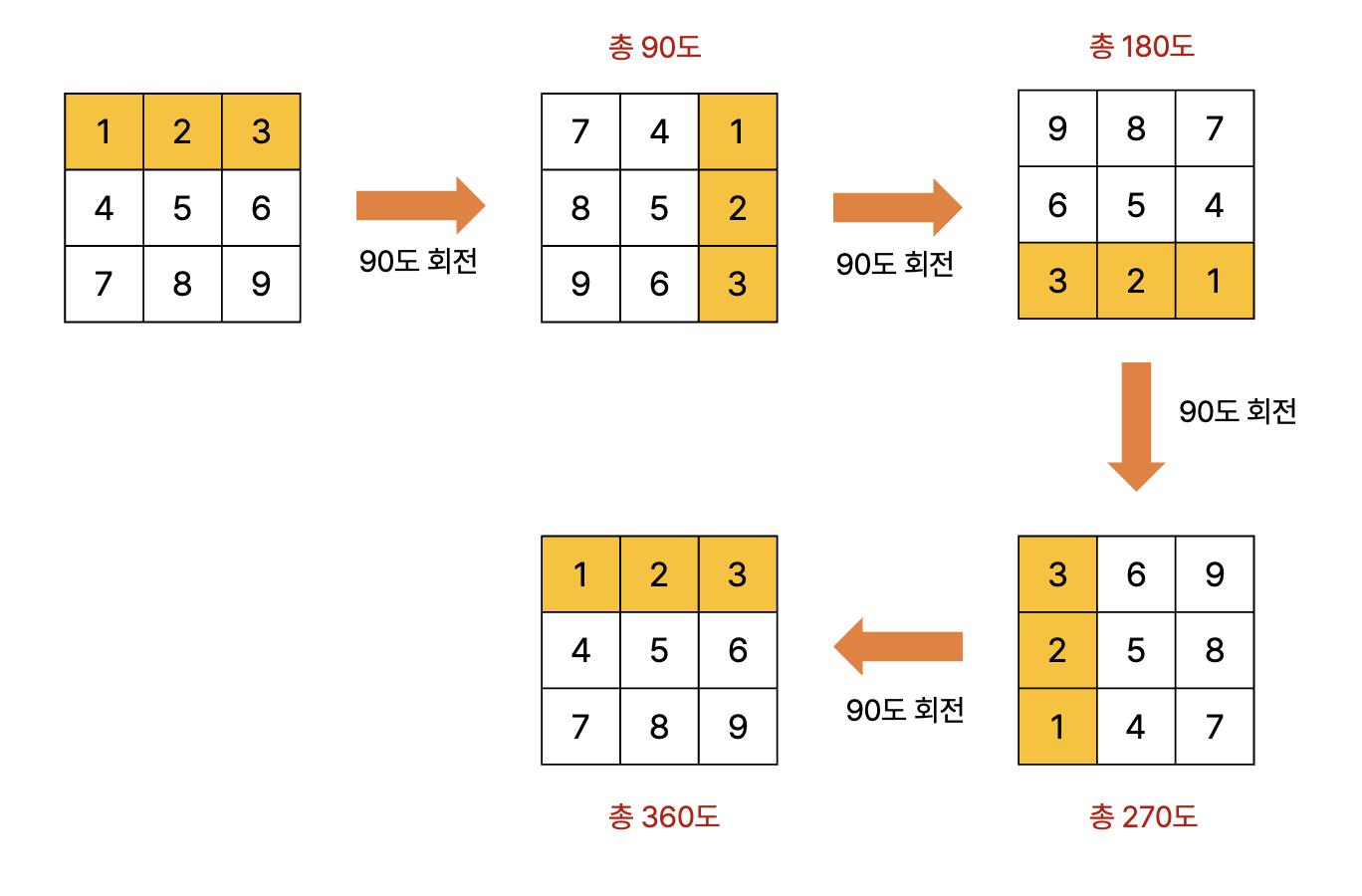
2차원 배열 회전 알고리즘

• 행과 열의 수가 같은 정방형 배열(square array 또는 square matrix) 에서 아래 그림과 같이 2차원 배열을 오른쪽으로 90도 회전 시키는 코드를 구현해보자.
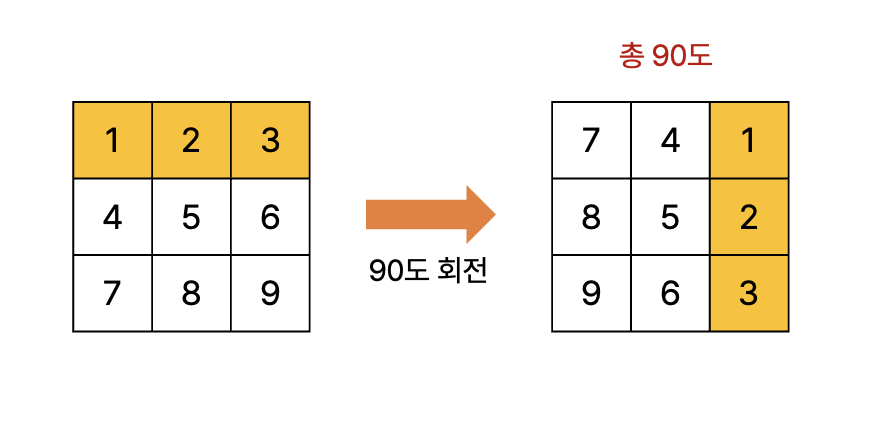
• 하이라이팅 되어 있는 [1, 2, 3] 을 통해 회전 방향을 자세히 살펴보자.

90도 회전

N	Before	After
1	(0, 0)	(0, 2)
2	(0, 1)	(1, 2)
3	(0, 2)	(2, 2)

• [1, 2, 3] 의 위치 변화를 확인하면 규칙을 찾을 수 있다.
  • 회전 전의 열 번호와 회전 후의 행 번호가 일치한다.
  • 회전 후의 열은 N-1 에서 회전 전의 행을 뺀 값과 같다.
• 코드로 작성해보면 다음과 같다.
  • 입력 받은 2차원 배열은 m 이고, 반환할 배열은 ret 으로 정의한다.
  • 배열의 행과 열의 크기는 N 이다.

def rotate_90(m):
    N = len(m)
    ret = [[0] * N for _ in range(N)]

    for r in range(N):
        for c in range(N):
            ret[c][N-1-r] = m[r][c]
    return ret

test = [[1,2,3], [4,5,6], [7,8,9]]
print(rotate_90(test))  # [[7, 4, 1], [8, 5, 2], [9, 6, 3]]

180도 회전

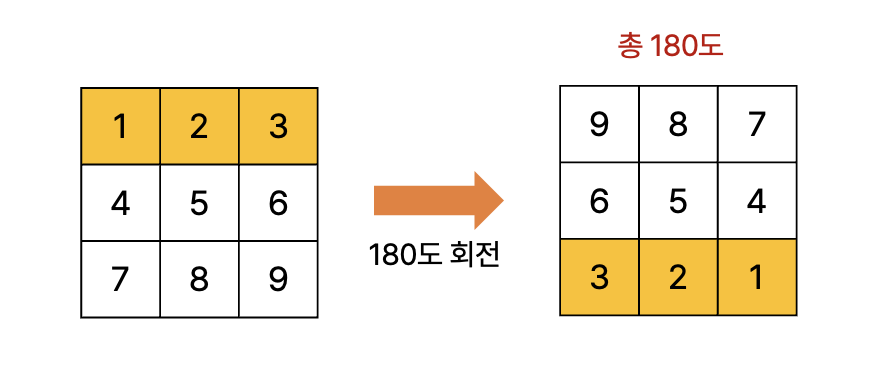
• 마찬가지로 [1, 2, 3]의 위치 변화를 살펴보자.

N	Before	After
1	(0, 0)	(2, 2)
2	(0, 1)	(2, 1)
3	(0, 2)	(2, 0)

• 규칙성은 다음과 같다.
  • 회전 후의 행 번호는 N-1 의 값에서 전의 행 번호를 뺀 것과 같다.
  • 회전 후의 열 번호는 N-1 의 값에서 전의 열 번호를 뺀 것과 같다.
• 코드로 작성해보자.

def rotate_180(m):
    N = len(m)
    ret = [[0] * N for _ in range(N)]

    for r in range(N):
        for c in range(N):
            ret[N-1-r][N-1-c] = m[r][c]
    return ret

test = [[1,2,3], [4,5,6], [7,8,9]]
print(rotate_180(test))  # [[9, 8, 7], [6, 5, 4], [3, 2, 1]]

270도 회전

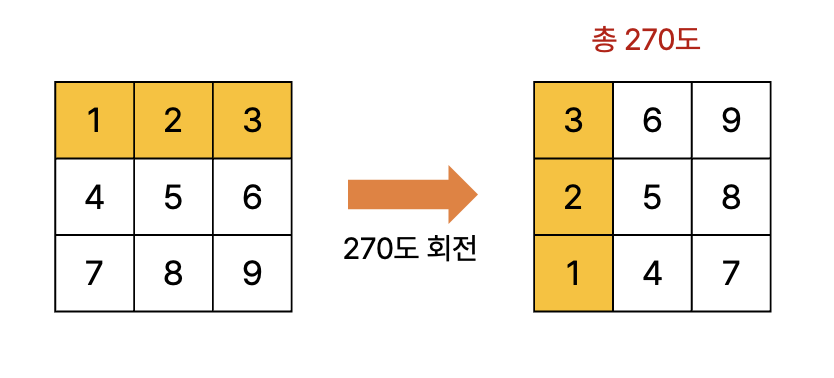
• 마찬가지로 [1, 2, 3]의 위치 변화를 살펴보자.

N	Before	After
1	(0, 0)	(2, 0)
2	(0, 1)	(1, 0)
3	(0, 2)	(0, 0)

• 규칙성은 다음과 같다.
  • 회전 후의 열과 전의 행이 일치한다.
  • 후의 행 번호는 N-1 에서 전의 열 번호를 뺀 값과 일치한다.
• 코드로 작성해보자.

def rotate_270(m):
    N = len(m)
    ret = [[0] * N for _ in range(N)]

    for r in range(N):
        for c in range(N):
            ret[N-1-c][r] = m[r][c]
    return ret

test = [[1,2,3], [4,5,6], [7,8,9]]
print(rotate_270(test))  # [[3, 6, 9], [2, 5, 8], [1, 4, 7]]

전체 코드 작성하기

• 위에서 작성한 코드를 바탕으로, 90도 단위로 2차원 정방형 배열을 회전시키는 전체 코드를 작성해보자.
  • 입력 받은 2차원 배열은 m 이고, 반환할 배열은 ret 으로 정의한다.
  • 90도 단위로 회전시킬 d 도 입력받는다. (총 90*d도 회전)

def rotate(m, d):

    N = len(m)
    ret = [[0] * N for _ in range(N)]

    if d % 4 == 1:
        for r in range(N):
            for c in range(N):
                ret[c][N-1-r] = m[r][c]
    elif d % 4 == 2:
        for r in range(N):
            for c in range(N):
                ret[N-1-c][N-1-r] = m[r][c]
    elif d % 4 == 3:
        for r in range(N):
            for c in range(N):
                ret[N-1-c][r] = m[r][c]
    else:
        for r in range(N):
            for c in range(N):
                ret[r][c] = m[r][c]

    return ret

zip() 사용하기

• 파이썬의 내장함수 zip() 을 사용하면 위에서 구현한 회전 알고리즘을 더 쉽게 구현할 수 있다.

zip(*iterable)

• 동일한 개수로 이루어진 자료형을 묶어주는 역할을 하는 함수이다.
• iterable(반복 가능한) 자료형의 개수가 동일할 때 사용할 수 있다.
• 리스트의 원소를 하나씩 꺼내서 새로운 리스트를 만든다.

a = list(zip([1, 2, 3], [4, 5, 6]))
b = list(zip("abc", "def"))

print(a)  # [(1, 4), (2, 5), (3, 6)]
print(b)  # [('a', 'd'), ('b', 'e'), ('c', 'f')]

2차원 배열 90도 회전하기

• 시계 방향

lst = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
rotate_90 = list(map(list, zip(*lst[::-1])))

print(rotate_90)  # [[7, 4, 1], [8, 5, 2], [9, 6, 3]]

• 반시계 방향

lst = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
rotate_90 = list(map(list, zip(*lst)))[::-1]

print(rotate_90)  # [[3, 6, 9], [2, 5, 8], [1, 4, 7]]

전치 행렬 만들기

• zip()을 사용하면 행과 열을 뒤집은 전치 행렬도 쉽게 만들 수 있다 !

lst = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
reversed_lst = list(map(list, zip(*lst)))

print(reversed_lst)  # [[1, 4, 7], [2, 5, 8], [3, 6, 9]]

응용 문제 - 프로그래머스 : 자물쇠와 열쇠

문제 링크

접근 방법

• key 배열과 lock 배열 범위가 모두 3 ≤ N, M ≤ 20 으로 크지 않아 시간 복잡도를 고려하지 않고, 완전 탐색으로 구현

1. key 배열을 90 도 씩 시계 방향으로 회전 한다. → 2차원 배열을 회전하는 함수 작성
2. 자물쇠를 끼워 맞춘다.
   1. 모든 경우의 수를 확인하기 위해서는 그림과 같이 자물쇠 배열 크기를 3배 확장 시킨후 맨 왼쪽 위부터 맨 오른쪽 아래까지 자물쇠를 모두 끼워 맞추는 경우를 확인해야 한다.
   2. lock[M-1][M-1] 이 key[0][0] 과 맞는 부분부터 lock[0][0] 이 key[N-1][N-1] 과 맞는 부분까지 전부 확인

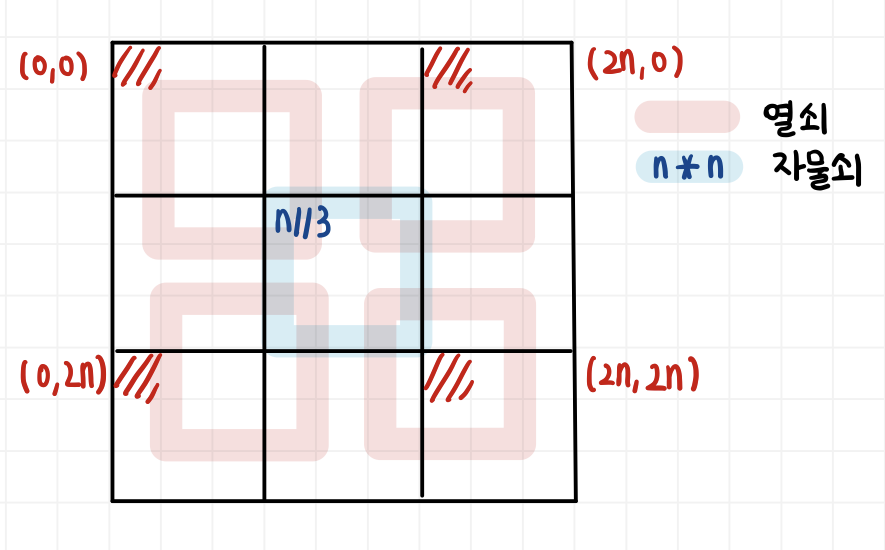
3. 끼워 맞춘 후의 자물쇠의 모든 원소가 1이면 자물쇠를 열 수 있는 것이므로 True 를 반환한다. → 모든 원소가 1인지 확인하는 함수 작성
   1. 끼워 맞춘 부분을 확인할 때는 확장시킨 배열의 가운데 부분만 확인하면 된다.
   2. 끼워 맞춘 부분을 확인한 이후에는 다시 이전으로 돌아가는 과정이 필요하기 때문에, 깊은 복사를 활용해서 이전 배열을 백업해 두고, 확인한 다음에 다시 돌아가는 방법을 사용했다.

구현 코드 1 - 회전 함수 직접 구현

# n*n 2차원 배열을 시계방향으로 90*d 도 회전시키는 함수
def rotate(array, d):
    N = len(array)
    ret = [[0] * N for _ in range(N)]
    if d % 4 == 1:  # 90 도
        for i in range(N):
            for j in range(N):
                ret[j][N - 1 - i] = array[i][j]
    elif d % 4 == 2:  # 180 도
        for i in range(N):
            for j in range(N):
                ret[N - 1 - i][N - 1 - j] = array[i][j]
    elif d % 4 == 3:  # 270 도
        for i in range(N):
            for j in range(N):
                ret[N - 1 - j][i] = array[i][j]
    else:  # 360도
        for i in range(N):
            for j in range(N):
                ret[i][j] = array[i][j]
    return ret

# 자물쇠 중간 부분이 모두 1인지 확인
def check(array):
    N = len(array) // 3
    for i in range(N, N*2):
        for j in range(N, N*2):
            if array[i][j] != 1:
                return False
    return True

def solution(key, lock):
    M = len(key)
    N = len(lock)

    # 자물쇠보다 3배 큰 배열 생성
    new_lock = [[0]*(N*3) for _ in range(N*3)]
    # 가운데에 자물쇠 넣기
    for i in range(N):
        for j in range(N):
            new_lock[N+i][N+j] = lock[i][j]

    # 열쇠를 넣는 모든 경우의 수 확인
    for i in range(0, 2*N):
        for j in range(0, 2*N):
            # 열쇠를 4방향으로 회전
            for d in range(4):
                rotate_key = rotate(key, d)
                # 열쇠 맞추기 전 배열 백업 해두기 - 깊은 복사
                back_up = [lst[:] for lst in new_lock]
                # 열쇠 맞추기
                for y in range(M):
                    for x in range(M):
                        new_lock[i+y][j+x] += rotate_key[y][x]
                # 열쇠 맞는지 확인
                if check(new_lock):
                    return True
                # 다시 열쇠 맞추기 전으로 돌리기
                new_lock = [lst[:] for lst in back_up]

    # 끝까지 True 를 반환하지 못하면 실패
    return False

구현 코드 2 - zip() 사용

# solve 2
def rotate_by_zip(array, d):
    ret = array
    for i in range(d):
        ret = list(map(list, zip(*array[::-1])))
        array = ret
    return ret

# 자물쇠 중간 부분이 모두 1인지 확인
def check(array):
    N = len(array) // 3
    for i in range(N, N*2):
        for j in range(N, N*2):
            if array[i][j] != 1:
                return False
    return True

def solution(key, lock):
    M = len(key)
    N = len(lock)

    # 자물쇠보다 3배 큰 배열 생성
    new_lock = [[0]*(N*3) for _ in range(N*3)]
    # 가운데에 자물쇠 넣기
    for i in range(N):
        for j in range(N):
            new_lock[N+i][N+j] = lock[i][j]

    # 열쇠를 넣는 모든 경우의 수 확인
    for i in range(0, 2*N):
        for j in range(0, 2*N):
            # 열쇠를 4방향으로 회전
            for d in range(4):
                rotate_key = rotate_by_zip(key, d)
                # 열쇠 맞추기 전 배열 백업 해두기 - 깊은 복사
                back_up = [lst[:] for lst in new_lock]
                # 열쇠 맞추기
                for y in range(M):
                    for x in range(M):
                        new_lock[i+y][j+x] += rotate_key[y][x]
                # 열쇠 맞는지 확인
                if check(new_lock):
                    return True
                # 다시 열쇠 맞추기 전으로 돌리기
                new_lock = [lst[:] for lst in back_up]

    # 끝까지 True 를 반환하지 못하면 실패
    return False

Tip. 2차원 배열 깊은 복사

• deepcopy 모듈 사용

import copy
a = [[1,2],[3,4]]
b = copy.deepcopy(a)

• slicing 사용
  • deepcopy 보다 빠름

a = [[1, 2], [3, 4]]
b = [arr[:] for arr in a]

References

• [Python] 2차원 배열 회전 알고리즘
• [Python] zip() 이용해서 2차원 리스트 회전하기