⭐️ 플로이드 워셜 알고리즘(Floyd-Warshall Algorithm)

• 모든 지점에서 다른 모든 지점까지 최단 경로를 모두 구해야하는 경우 사용
• 다익스트라 알고리즘과 마찬가지로 단계마다 '거쳐가는 노드'를 기준으로 알고리즘 수행
  • 매번 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다는 점이 다익스트라 알고리즘과 다름
• 노드의 개수가 N개일 때 알고리즘상으로 N번의 단계를 수행하며, 단계마다 $O(N^2)$의 연산을 통해 현재 노드를 거쳐가는 모든 경로를 고려
  • 따라서 플로이드 워셜 알고리즘의 총 시간복잡도는 $O(N^3)$
• 다익스트라 알고리즘에서는 출발 노드가 1개이므로 다른 모든 노드까지의 최단 거리를 저장하기 위해 1차원 리스트 이용
  • 반면 플로이드 워셜 알고리즘은 2차원 리스트에 최단거리 정보 저장
  • 모든 노드에 대하여 다른 모든 노드로 가는 최단 거리 정보를 담아야 하기 때문
  • 2차원 리스트를 처리해야 하므로 N번의 단계에서 매번 $O(N^2)$의 시간이 소요
• 다익스트라 알고리즘은 그리디 알고리즘이지만 플로이드 워셜 알고리즘은 다이나믹 프로그래밍
  • 노드의 개수가 N이라고 할 때, N번 만큼의 단계를 반복하며 점화식에 맞게 2차원 리스트를 갱신하기 때문

점화식

• 알고리즘 각 단계에서는 현재 확인하고 있는 노드를 제외하고, N-1개의 노드 중에서 서로 다른 노드 (A,B)쌍을 선택한다.
  • 이후에 A → 1번 노드 → B로 가는 비용을 확인한 뒤에 최단 거리를 갱신한다.
  • $_{N-1}P_2$ 개의 쌍을 단계마다 반복해서 확인
  • $O(_{N-1}P_2)$는 $O(N^2)$이라고 생각할 수 있으므로 전체 시간 복잡도는 $O(N^3)$
• K번의 단계에 대한 점화식은 다음과 같다.
  $D_{ab} = min(D_{ab}, D_{ak}+D_{kb})$
• A에서 B로 가는 최소비용과 A에서 K를 거쳐 B로 가는 비용을 비교하여 더 작은 값으로 갱신한다.
  • 즉, 바로 이동하는 거리가 특정한 노드를 거쳐서 이동하는 거리보다 더 많은 비용을 가진다면 이를 더 짧은 것으로 갱신
• 전체적으로 3중 반복문을 이용하여 점화식에 따라 최단 거리 테이블을 갱신하면 문제를 해결할 수 있다.

그림으로 이해하기

• 아래와 같은 그래프가 있다고 가정해보자.

STEP 0

• 초기 테이블 설정하기
• 2차원 리스트에서 각 값에 해당하는 $D_{ab}$는 a에서 b로 가는 최단 거리이다.
• 그래프에서 연결된 간선은 단순히 그 값을 채워 넣고 연결되지 않은 간선은 '무한' 값을 넣는다.
• 자기 자신으로 가는 비용은 0이므로, $1≤i≤n$의 범위를 가지는 모든 $i$에 대하여 $D_{ii}$는 0으로 초기화

STEP 1

• 1번 노드를 거쳐 가는 경우 계산
• 2번 노드를 제외한 2, 3, 4번 노드에서 2개의 노드를 뽑는 경우를 고려
  • (2, 3), (2, 4), (3, 2), (3, 4), (4, 2), (4, 3)
• 아래 6가지 경우를 확인하며 값을 계산하여 갱신
  $D_{23} = min(D_{23}, D_{21}+D_{13})$
  $D_{24} = min(D_{24}, D_{21}+D_{14})$
  $D_{32} = min(D_{32}, D_{31}+D_{12})$
  $D_{34} = min(D_{34}, D_{31}+D_{14})$
  $D_{42} = min(D_{42}, D_{41}+D_{12})$
  $D_{43} = min(D_{43}, D_{41}+D_{13})$

STEP 2

• 2번 노드를 거쳐 가는 경우 계산
• 2번 노드를 제외한 1, 3, 4번 노드에서 2개의 노드를 뽑는 경우를 고려
  • (1, 3), (1, 4), (3, 1), (3, 4), (4, 1), (4, 3)
• 아래 6가지 경우를 확인하며 값을 계산하여 갱신
  $D_{13} = min(D_{13}, D_{12}+D_{23})$
  $D_{14} = min(D_{14}, D_{12}+D_{24})$
  $D_{31} = min(D_{31}, D_{32}+D_{21})$
  $D_{34} = min(D_{34}, D_{32}+D_{24})$
  $D_{41} = min(D_{41}, D_{42}+D_{21})$
  $D_{43} = min(D_{43}, D_{42}+D_{23})$

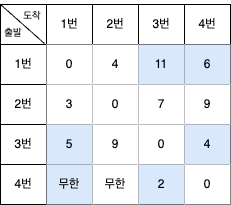
STEP 3

• 3번 노드를 거쳐 가는 경우 계산
• 3번 노드를 제외한 1, 2, 4번 노드에서 2개의 노드를 뽑는 경우를 고려
  • (1, 2), (1, 4), (2, 1), (2, 4), (4, 1), (4, 2)
• 아래 6가지 경우를 확인하며 값을 계산하여 갱신
  $D_{12} = min(D_{12}, D_{13}+D_{32})$
  $D_{14} = min(D_{14}, D_{13}+D_{34})$
  $D_{21} = min(D_{21}, D_{23}+D_{31})$
  $D_{24} = min(D_{24}, D_{23}+D_{34})$
  $D_{41} = min(D_{41}, D_{43}+D_{31})$
  $D_{42} = min(D_{42}, D_{43}+D_{32})$

STEP 4

• 4번 노드를 거쳐가는 경우 계산
• 4번 노드를 제외한 1, 2, 3번 노드에서 2개의 노드를 뽑는 경우를 고려
  • (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)
• 아래 6가지 경우를 확인하며 값을 계산하여 갱신
  $D_{12} = min(D_{12}, D_{14}+D_{42})$
  $D_{13} = min(D_{13}, D_{14}+D_{43})$
  $D_{21} = min(D_{21}, D_{24}+D_{41})$
  $D_{23} = min(D_{23}, D_{24}+D_{43})$
  $D_{31} = min(D_{31}, D_{34}+D_{41})$
  $D_{32} = min(D_{32}, D_{34}+D_{42})$

최종 결과

• 모든 노드에서 모든 노드로 가는 최단 거리 정보를 담은 테이블

✏️ 구현하기

1. 초기에는 각 노드 쌍 사이의 거리를 무한으로 설정하고 자기 자신으로 가는 거리는 0으로 설정한다.
2. 입력으로 주어진 간선 정보를 바탕으로 그래프를 초기화한다.
3. 플로이드 워셜 알고리즘을 사용하여 최단 경로를 구한다.
   • 중간 노드를 거쳐서 가는 경로가 더 짧은 경우, 해당 경로로 거리를 갱신한다.
4. 최단 경로를 출력한다.
   • 도달할 수 없는 경우 "INFINITY"를 출력하고, 도달할 수 있는 경우에는 최단 거리를 출력한다.

• Python으로 작성한 플로이드워셜 알고리즘은 다음과 같다. (코드 출처)

INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수 및 간선의 개수를 입력받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]

# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
    for b in range(1, n + 1):
        if a == b:
            graph[a][b] = 0

# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
    # A에서 B로 가는 비용은 C라고 설정
    a, b, c = map(int, input().split())
    graph[a][b] = c

# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
    for a in range(1, n + 1):
        for b in range(1, n + 1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

# 수행된 결과를 출력
for a in range(1, n + 1):
    for b in range(1, n + 1):
        # 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
        if graph[a][b] == 1e9:
            print("INFINITY", end=" ")
        # 도달할 수 있는 경우 거리를 출력
        else:
            print(graph[a][b], end=" ")
    print()

• 위에서 살펴본 예제를 입력한 결과는 다음과 같다.

4
7
1 2 4
1 4 6
2 1 3
2 3 7
3 1 5
3 4 4
4 3 2

0 4 8 6
3 0 7 9
5 9 0 4
7 11 2 0

📍 References

• 이것이 취업을 위한 코딩테스트다 - 나동빈 저
• https://www.youtube.com/watch?v=9574GHxCbKc