⭐️ 투 포인터(Two Pointers) 알고리즘

• 투 포인터(Two Pointers) 알고리즘은 리스트에 순차적으로 접근해야 할 때 2개의 점의 위치를 기록하면서 처리하는 알고리즘을 의미한다.
• 예를 들어 한 반에 40명이 있을 때, 모든 학생을 번호 순서대로 일렬로 세운 뒤 학생들을 순차적으로 지목해야 할 경우를 생각해보자.
  • 우리는 번호로 한명씩 부르기 보다는 '2번부터 7번까지의 학생'이라고 부를 수도 있다.
  • 이처럼 리스트에 담긴 데이터에 순차적으로 접근해야할 때는 시작점과 끝점 2개의 점으로 접근할 데이터의 범위를 표현할 수 있다.
• 투포인터를 사용하여 풀 수 있는 대표적인 문제는 다음과 같다.
  • 특정한 합을 가지는 부분 연속 수열 찾기
  • 정렬되어 있는 두 리스트의 합집합 구하기

💫 특정한 합을 가지는 부분 연속 수열 찾기

• 이 문제는 양의 정수로만 구성된 리스트가 주어졌을 때, 그 부분 연속 수열 중에서 특정한 합을 갖는 수열의 개수를 출력하는 문제이다.
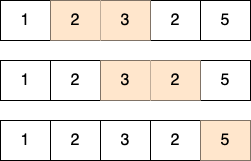
• 예를 들어, 다음과 같이 1, 2, 3, 2, 5를 차례대로 원소로 갖는 리스트가 주어져 있다고 해보자.

• 이 때 합계 값을 5라고 설정하면, 다음과 같은 3가지 경우의 수만 존재한다.

투 포인터 알고리즘을 이용하여 풀어보자.

• 투포인터 알고리즘의 특징은 2개의 변수를 이용해 리스트 상의 위치를 기록한다는 점이다.
• 이 문제에서는 부분 연속 수열의 시작점(start)과 끝점(end)의 위치를 기록한다.
• 특정한 부분합을 M이라고 할 때, 구체적인 알고리즘은 다음과 같다.
  1. 시작점(start)과 끝점(end)이 첫 번째 원소의 인덱스(0)을 가리키도록 한다.
  2. 현재 부분합이 M과 같다면 카운트 한다.
  3. 현재 부분합이 M보다 작으면 end를 1 증가시킨다.
  4. 현재 부분합이 M보다 크거나 같으면 start를 1 증가시킨다.
  5. 모든 경우를 확인할 때까지 2번부터 4번까지의 과정을 반복한다.

그림으로 이해하기

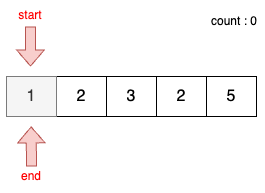
STEP 0

• 초기 단계에서는 시작점과 끝 점이 첫번째 원소의 인덱스를 가리키도록 한다.
• 이때 현재의 부분합은 1이므로 무시한다.

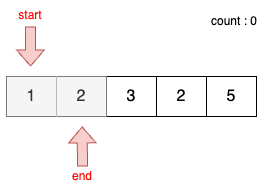
STEP 1

• 이전 단계에서 부분합이 1이었기 때문에 end를 1 증가시킨다.
• 현재 부분합은 3이므로 이번에도 마찬가지로 무시한다.

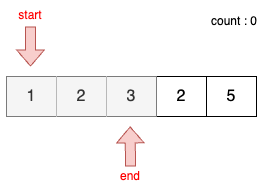
STEP 2

• 이전 단계에서 부분합이 3이었기 때문에 end를 1 증가시킨다.
• 현재 부분합은 6이므로 이번에도 마찬가지로 무시한다.

STEP 3

• 이전 단계에서 부분합이 6이었기 때문에 start를 1 증가시킨다.
• 현재 부분합은 5이므로 카운트 한다.

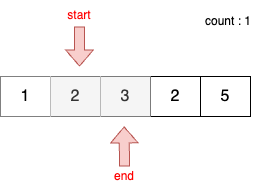
STEP 4

• 이전 단계에서 부분합이 5이었기 때문에 start를 1 증가시킨다.
• 현재 부분합은 3이므로 무시한다.

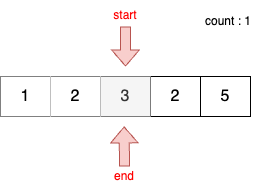
STEP 5

• 이전 단계에서 부분합이 3이었기 때문에 end를 1 증가시킨다.
• 현재 부분합은 5이므로 카운트 한다.

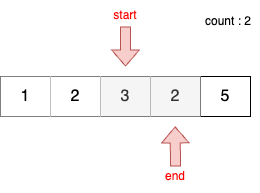
STEP 6

• 이전 단계에서 부분합이 5이었기 때문에 start를 1 증가시킨다.
• 현재 부분합은 2이므로 무시한다.

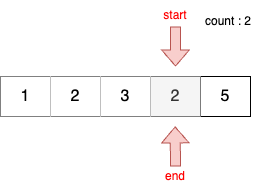
STEP 7

• 이전 단계에서 부분합이 2이었기 때문에 end를 1 증가시킨다.
• 현재 부분합은 7이므로 무시한다.

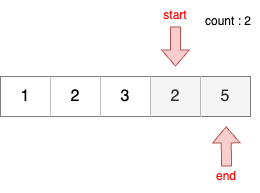
STEP 8

• 이전 단계에서 부분합이 7이었기 때문에 start를 1 증가시킨다.
• 현재 부분합은 5이므로 카운트 한다.
• 결과적으로 부분합이 5가 되는 부분 연속 수열의 개수는 3개이다.

코드 작성하기

• 이 문제를 투포인터 알고리즘으로 해결할 수 있는 이유는 기본적으로 시작점을 오른쪽으로 이동시키면 항상 합이 감소하고, 끝점을 오른쪽으로 이동시키면 항상 합이 증가하기 때문이다.
  • 따라서 만약에 리스트 내 원소에 음수 데이터가 포함되어 있는 경우에는 투 포인터 알고리즘으로 해결할 수 없다.
• 시작점(start)을 반복문을 이용하여 증가시키며, 증가할 때마다 끝점(end)을 그것에 맞게 증가시키는 방식으로 구현한 코드는 다음과 같다. (코드 출처)

N = int(input())  # 데이터의 개수
M = int(input())  # 찾고자 하는 부분합
data = list(map(int, input().split()))  # 전체 수열

cnt = 0
interval_sum = 0
end = 0

# start를 차례대로 증가시키며 반복
for start in range(N):
    # end를 가능한 만큼 이동시키기
    while interval_sum < M and end < N:
        interval_sum += data[end]
        end += 1
    # 부분합이 M일 때 카운트 증가
    if interval_sum == M:
        cnt += 1
    interval_sum -= data[start]

print(cnt)

• 위에서 살펴본 예시를 테스트한 결과는 다음과 같다.

5
5
1 2 3 2 5

3

💫 정렬되어 있는 두 리스트의 합집합 구하기

• 이미 정렬되어 있는 2개의 리스트가 주어지고, 두 리스트의 모든 원소를 합쳐서 정렬한 결과를 출력하는 문제이다.
• 이 문제를 풀기 위해서는 2개의 리스트 A, B가 주어졌을 때, 2개의 포인터를 이용하여 각 리스트에서 처리되지 않은 원소 중 가장 작은 원소를 가리키면 된다.
• 기본적으로 이미 정렬된 결과가 주어지므로 A, B의 원소를 앞에서부터 확인하면 된다.

알고리즘을 작성해보면,

1. 정렬된 리스트 A, B를 입력받는다.
2. 리스트 A에서 처리되지 않은 원소 중 가장 작은 원소를 i가 가리키도록 한다.
3. 리스트 B에서 처리되지 않은 원소 중 가장 작은 원소를 j가 가리키도록 한다.
4. A[i]와 B[j] 중에서 더 작은 원소를 결과 리스트에 담는다.
5. 리스트 A, B에서 더이상 처리할 원소가 없을 때까지 1~4번의 과정을 반복한다.

그림으로 이해하기

STEP 0

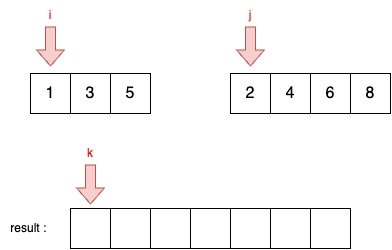
• 두 리스트의 모든 원소가 들어갈 수 있는 크기의 결과 리스트를 생성한다.
• i가 리스트 A의 첫 번째 원소를, j가 리스트 B의 첫 번째 원소를 가리키도록 한다.

STEP 1

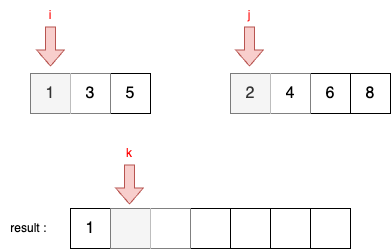
• 현재 i와 j가 가리키고 있는 두 원소를 비교한다. A[i] = 1, B[j] = 2이다.
• A[i] < B[j] 이므로 결과 리스트에 i가 가리키고 있는 원소를 담는다.
• 이후에 i를 1 증가시킨다.

STEP 2

• 현재 i와 j가 가리키고 있는 두 원소를 비교한다. A[i] = 3, B[j] = 2이다.
• A[i] > B[j] 이므로 결과 리스트에 j가 가리키고 있는 원소를 담는다.
• 이후에 j를 1 증가시킨다.

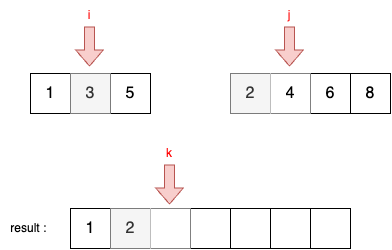
STEP 3

• 현재 i와 j가 가리키고 있는 두 원소를 비교한다. A[i] = 3, B[j] = 4이다.
• A[i] < B[j] 이므로 결과 리스트에 i가 가리키고 있는 원소를 담는다.
• 이후에 i를 1 증가시킨다.

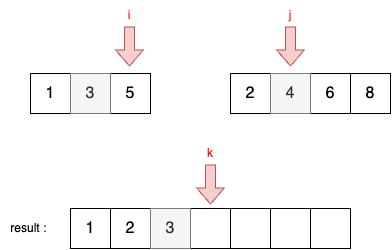
STEP 4

• 현재 i와 j가 가리키고 있는 두 원소를 비교한다. A[i] = 5, B[j] = 4이다.
• A[i] > B[j] 이므로 결과 리스트에 j가 가리키고 있는 원소를 담는다.
• 이후에 j를 1 증가시킨다.

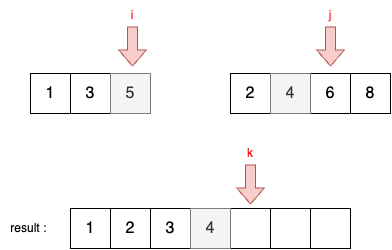
STEP 5

• 현재 i와 j가 가리키고 있는 두 원소를 비교한다. A[i] = 5, B[j] = 6이다.
• A[i] < B[j] 이므로 결과 리스트에 i가 가리키고 있는 원소를 담는다.
• 이후에 i를 1 증가시킨다.

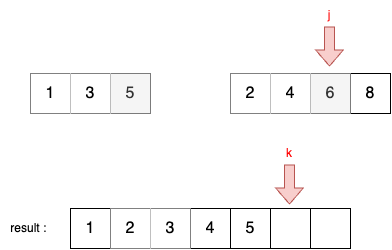
STEP 6

• 이제 리스트 A에 있는 모든 원소가 결과 리스트에 담겼으므로, 남은 리스트 B에 있는 모든 원소를 리스트에 담는다.
• 먼저 j가 가리키는 원소를 결과리스트에 담고, j를 1 증가시킨다.

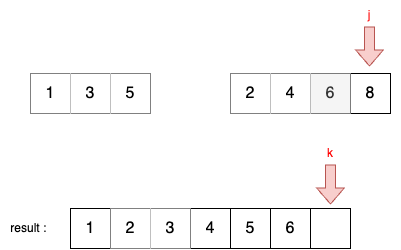
STEP 7

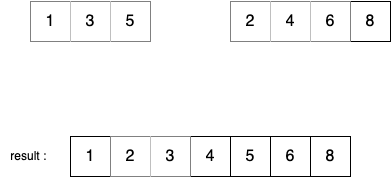
• 리스트 B의 마지막 원소까지 결과 리스트에 담는다.
• 최종적으로 겨로가리스트에는 두 리스트의 모든 원소가 정렬된 형태로 저장된 것을 확인할 수 있다.

코드 작성하기

• 결과적으로 정렬된 리스트 A와 B의 데이터 개수가 각각 N, M이라고 할 때, 이 알고리즘의 시간복잡도는 O(N+M)이다.
• 이 알고리즘은 병합정렬과 같은 일부 알고리즘에서 사용된다.
• 코드로 구현하면 다음과 같다. (코드 출처)

# 사전에 정렬된 리스트 A와 B 선언
n, m = map(int, input().split())  # 리스트 A, B의 크기
a = list(map(int, input().split()))
b = list(map(int, input().split()))

# 리스트 A와 B의 모든 원소를 담을 수 있는 크기의 결과 리스트 초기화
result = [0] * (n + m)
i = 0
j = 0
k = 0

# 모든 원소가 결과 리스트에 담길 때까지 반복
while i < n or j < m:
    # 리스트 B의 모든 원소가 처리되었거나, 리스트 A의 원소가 더 작을 때
    if j >= m or (i < n and a[i] <= b[j]):
        # 리스트 A의 원소를 결과 리스트로 옮기기
        result[k] = a[i]
        i += 1
    # 리스트 A의 모든 원소가 처리되었거나, 리스트 B의 원소가 더 작을 때
    else:
        # 리스트 B의 원소를 결과 리스트로 옮기기
        result[k] = b[j]
        j += 1
    k += 1

# 결과 리스트 출력
for i in result:
    print(i, end=' ')

• 위에서 살펴본 예시를 테스트한 결과는 다음과 같다.

3 4
1 3 5
2 4 6 8

1 2 3 4 5 6 8 

✏️ 문제 추천

• 백준 2018번 - 수들의 합 5
• 백준 2003번 - 수들의 합 2
• 백준 1208번 - 부분수열의 합
• 백준 1806번 - 부분합

📍 References

• 이것이 취업을 위한 코딩테스트다. - 나동빈 저
• https://www.youtube.com/watch?v=ttLRltNDiCo