컴퓨터에서 숫자를 표현하는 방법은?
사람은 10진법으로 숫자를 표현하지만,
컴퓨터는 2진법으로 숫자를 표현한다.
즉, 1, 0으로 모든 것을 받아 들인다.
왜냐하면 컴퓨터는 전기 신호로 모든 데이터를 처리한다.
전기 신호가 on이면 1으로,
전기 신호가 off이면 0으로 표현한다.
소수점은 어떻게 표현할까?
10진법의 숫자를 2진법으로 표현할 때 가장 문제가 되는 부분이 실수이다.
실수, 즉 0.1, 2.1과 같은 소수점을 2진법으로 정확하게 나타낼 수가 없다.
263 => 100000111
0.3 => 0.01001100110011........ (무한 반복....)
즉, 2진수로 표현하지 못하는 소수는 가장 근사치의 값으로 저장이 된다.
소수점을 저장하기 위한 방법
고정 소수점
정수를 표현하는 비트 수와 소수를 표현하는 비트 수를 미리 정해 놓고,
해당 비트 만큼만 사용해서 숫자를 표현하는 방식
예를 들어, 263.3이란 실수를 표현하는데 4byte(32bit)를 사용하고,
부호는 1bit, 정수는 16bit, 소수는 15bit를 사용하도록 약속한 시스템이 있다고 하자.
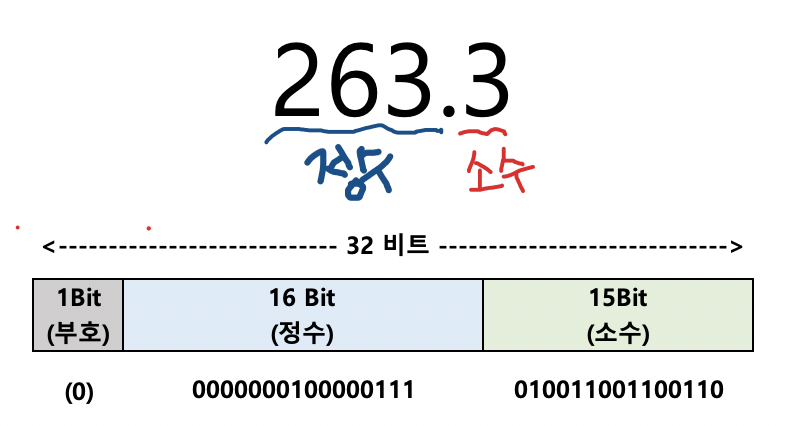
정수인 263을 2진법으로 바꿔서 16bit로 저장하고,
소수인 0.3을 2진법으로 바꿔서 15bit로 저장한다.
즉, 이런 시스템에서는 부호는 +이므로 0이 저장되고,
정수인 263은 16bit를 사용하므로, 0000000100000111이 저장되고,
소수인 0.3은 15bit를 사용하므로, 010011001100110으로 저장이 된다..
정수를 표현하는 bit를 늘리면 큰 숫자를 표현할 수 있지만, 정밀한 숫자는 표현이 어렵고,
소수를 표현하는 bit를 늘리면 정밀한 숫자를 표현할 수 있지만, 큰 숫자는 표현이 어렵다.
부동소수점(浮動小數點, floating point) : 실수를 컴퓨터상에서 근사하여 표현할 때 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적는 것
유효숫자를 나타내는 가수(假數)와 소수점의 위치를 풀이하는 지수(指數)로 나누어 표현
(浮 뜰 부 動 움직일 동) : 붙박여 있지 않고 떠서 움직임. 진득하지 못하고 들뜸.
IEEE 754 표준 방식으로 숫자를 부동소수점으로 표현하는 방법
(IEEE 754는 전기 전자 기술자 협회 (IEEE)에서 개발한 표준 부동소수점 방식이며 현재 컴퓨터에서 가장 널리 쓰이는 방식입니다.)
부호, 지수, 가수
IEEE 754 부동소수점 표현에서 숫자는 아래와 같이 부호부, 지수부, 가수부의 세 부분으로 구성됩니다.
각 부분의 역할과 사용하는 비트 수는 아래와 같습니다.
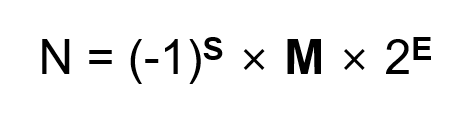
부호부 (Sign) : 1비트. 숫자의 부호를 나타내며, 양수일 때 0, 음수일 때1이 됩니다.
지수부 (Exponent) :8비트. 지수를 나타냅니다.
가수부 (Mantissa) : 23비트. 가수 또는 유효숫자를 나타냅니다.

위의 그림과 같이 숫자를 표현하고 저장하기 위해 32비트 (4바이트)를 사용하는 방식을 단정도 (single precision)라고 합니다.
배정도 (double precision) 표현에서는 64비트 (8바이트)를 사용합니다.
부동소수점 변환 예시
숫자 -314.625를 IEEE 754 부동소수점 방식으로 표현해 보겠습니다.
부호부
첫번째로 부호를 확인합니다.
부호가 음수이므로 32비트의 가장 앞자리는 1이 됩니다.

가수부
두번째로 숫자의 절대값을 2진수로 표현합니다.
314.625는 2진수 100111010.101 (2) 가 됩니다.
이 2진수의 소수점을 아래와 같이 왼쪽으로 이동시켜서 소수점 왼쪽에 1만 남도록 합니다.

이제 2진수 100111010.101 (2) 를 아래와 같이 표현할 수 있는데, 이 방식을 정규화된 표현 방식이라고 합니다.

그리고 소수점의 오른쪽 부분 00111010101을 가수부 23비트의 앞에서부터 채워줍니다.
남는 자리는 0으로 채워줍니다.

지수부
이제 지수부를 채울 차례입니다.
지수는 8입니다.
지수 8에 bias인 127을 더해줍니다. (bias는 2 k-1 로 주어지는데 k는 지수부의 비트수 8입니다.)
아래와 같이 8에 bias를 더한 135를 2진수로 변환합니다.

변환한 2진수 10000111 (2) 을 8비트 지수부에 채워줍니다.

위와 같은 과정을 통해 숫자 -314.625를 32비트 단정도 부동소수점 방식으로 표현하면 11000011100111010101000000000000가 됩니다.
출처
https://codetorial.net/articles/floating_point.html
Wikipedia - 부동소수점
https://velog.io/@thms200/%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EC%A0%90-0.1-0.1-02-jbk5jrde3a
