
그래프는 활용 예시를 떠올리기 가장 쉬운 ADT라고 생각한다. 지하철 노선, SNS 망, 공항 항로 등 그래프를 쉽게 접할 수 있다.
그래프라는 이름에서 x, y 축의 무언가를 떠올릴 수 있지만 그래프 ADT는 네트워크 모델이라고 생각해야 한다.
이번 포스팅에서는 이후 포스팅을 위해 그래프 자료형의 개념, 용어 등에 대해 정리하는 시간을 가지려 한다.
그래프 개념
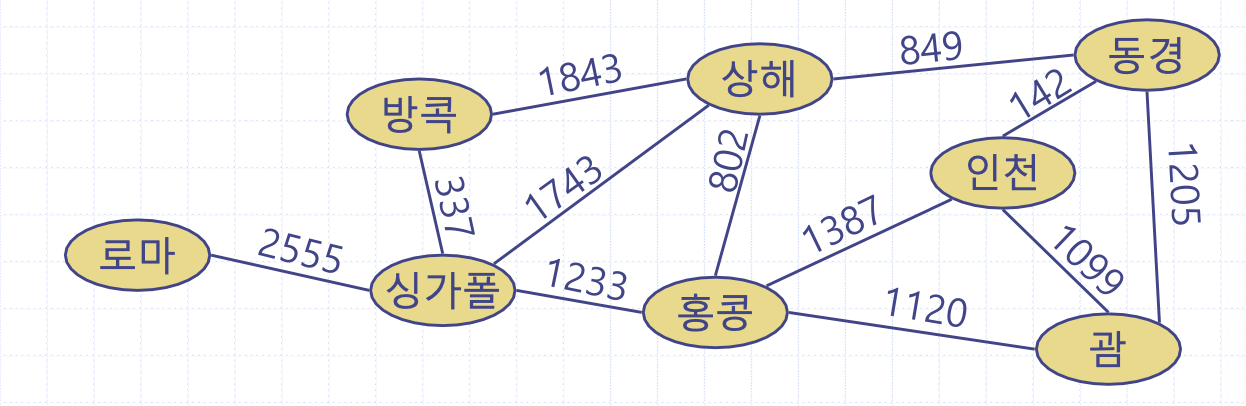
그래프는 정점과 간선의 쌍이다. 그림 예시에서 각 도시는 정점, 도시 간의 항로는 간선이 된다.
간선은 방향간선과 무방향간선으로 나뉜다. 무방향간선은 간선을 이루는 정점 간의 순서가 없는 것이고 방향 간선은 시점과 종점을 명시한다. 이에 따라 그래프도 방향그래프와 무방향그래프로 나뉜다.
그래프 용어
끝점(endpoint)
간선을 이루는 정점을 말한다. 임의의 간선 e의 끝점은 정점 v1, v2다.
부착 간선(incident)
정점에 붙어있는 간선을 말한다.
인접 정점(adjacent)
한 정점에 대해 간선으로 이어진 정점을 말한다. 임의의 간선 e의 끝점이 v1, v2라면, v2는 v1과 인접하다.
차수(degree)
정점에 연결된 간선의 개수를 정점의 차수라 한다.
병렬 간선(parallel edges)
양끝점을 공유하는 2개 이상의 간선을 뜻한다.
루프(loop)
끝점이 동일한 간선을 뜻한다.
경로(path)
정점에서 정점으로 가는 교대열이다.
ex) 출발 정점 - 간선 - 경유 정점 - 간선 - 도착 정점
단순 경로(simple path)
경로 상 모든 정점과 간선이 유일한 경로다.
싸이클(cycle)
출발 정점과 도착 정점이 같은 경로를 말한다.
단순 싸이클(simple cycle)
싸이클 경로 상 모든 정점과 간선이 유일한 싸이클이다.
단순 그래프(simple graph)
그래프 상 루프와 싸이클이 없는 그래프를 말한다.
부그래프(subgraph)
정점과 간선이 전체 그래프의 부분집합인 것이다.
신장부그래프(spanning subgraph)
정점을 모두 취하는 부그래프를 말한다. 신장은 모든 정점을 취하는 것을 의미한다.
연결 그래프(coonected graph)
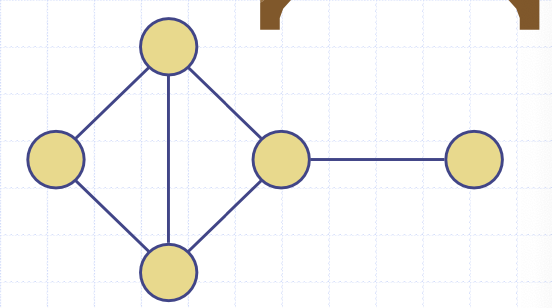
모든 정점 쌍에 대해 경로가 있는 그래프다.
트리(tree or free tree)
싸이클이 없는 연결 그래프를 말한다.
그래프의 트리는 루트 노드가 따로 있지 않다는 것이 자료구조에서 말하는 트리와의 차이점이다.
숲(forest)
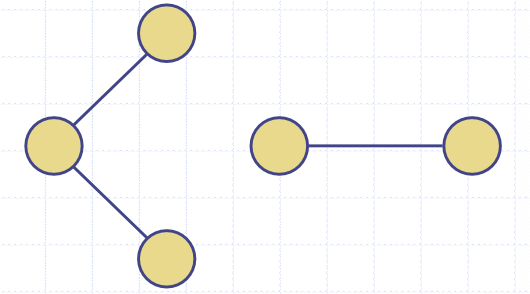
싸이클이 없는 무방향그래프를 말한다. 숲의 연결 요소들은 트리다.
신장트리(spanning tree)
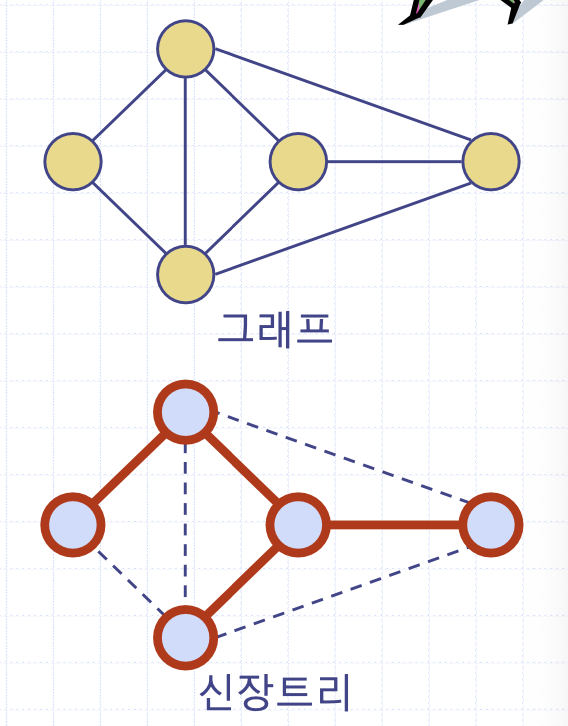
신장부그래프 중 트리인 것이다.
즉, 모든 정점을 취하는 부그래프 중 싸이클이 없는 것을 뜻한다.
신장숲(spanning forest)
신장부그래프 중 숲인 것이다.
그래프 속성
정점 수 : n, 간선 수: m
그래프의 모든 정점의 degree를 더하면 간선 2m이다.
- 각 간선이 2번 카운트 된다.
루프와 병렬 간선이 없는 무방향 그래프에서 m <= n C 2(조합)
- 최대로 간선이 많은 경우를 생각하자. 만약 n이 4라면, 그릴 수 있는 간선의 경우의 수는 4 C 2다.
- 서로 다른 4개 중 2개를 선택하는 것이기 때문에(확률과 통계 생각을 하자.) 최대 m은 6이다.
- 방향 그래프라면 m <= n P 2(순열)
그래프 구현
간선리스트 구조
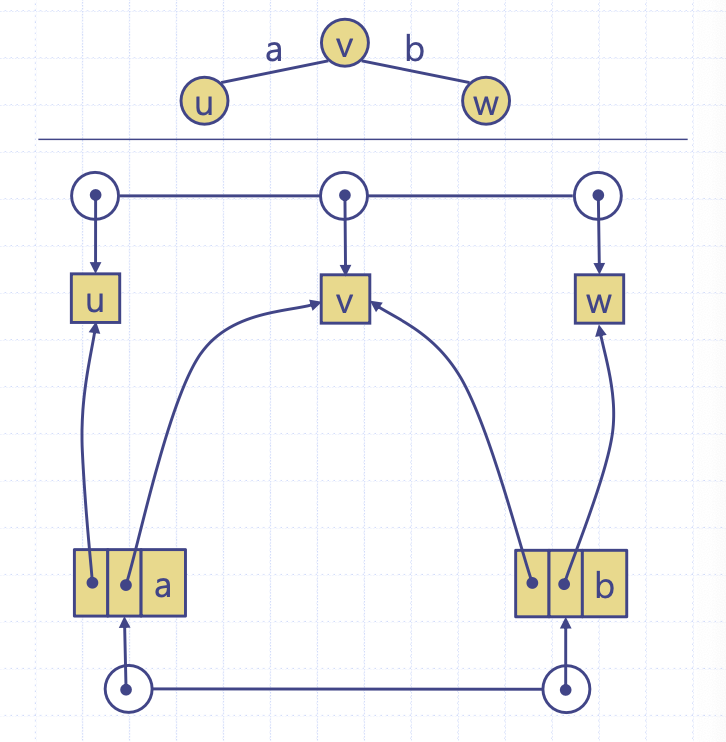
그래프 구현 중 가장 간단한 구조다.
정점 노드와 간선 노드를 각각 정점 리스트와 간선 리스트에 관리한다. 정점 노드에는 정점 원소에 대한 정보를 갖고 있고 간선 노드는 간선의 가중치 외에 간선의 endpoint를 포인터로 가리킨다.
간선리스트 구조는 단순하다는 장점이 있지만, v1과 v2가 인접한지에 대해 알아야 할 때 모든 간선을 다 뒤져봐야 하므로 O(m) 시간 걸리는 단점이 있다.
인접리스트 구조
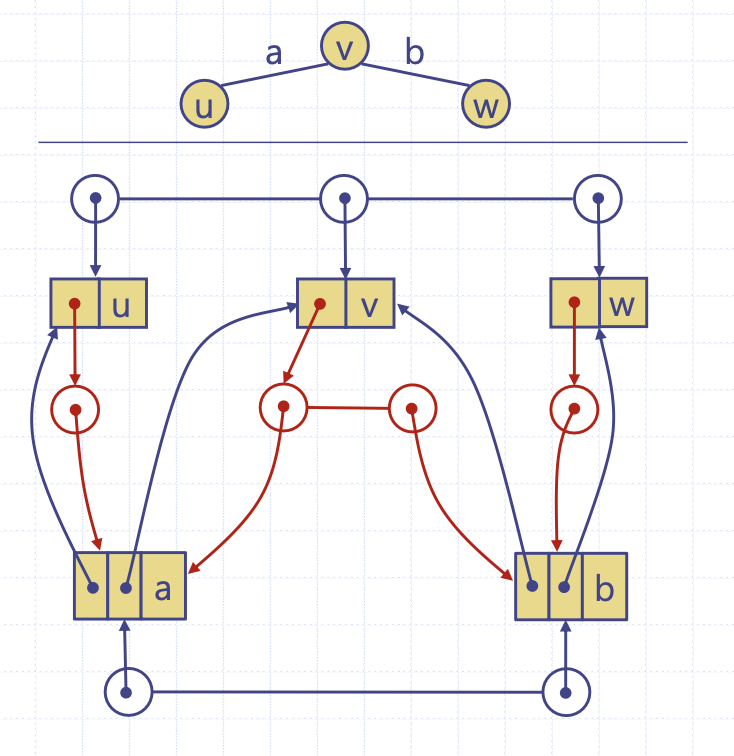
인접 리스트를 추가하여 정점 v의 인접 정보를 찾는 데에 O(degree(v))로 성능이 개선된다. 뭐 물론 한 정점에 모든 간선이 다닥다닥 붙어 있는 게 아닌 보편적인 경우를 생각했을 때 인접리스트 구조는 더 효율적이다.
인접리스트 구조는 무방향 그래프에서 두 개의 정점에 함께 표시해야 해서 표현에 따른 중복이 발생하긴 한다.
인접행렬 구조
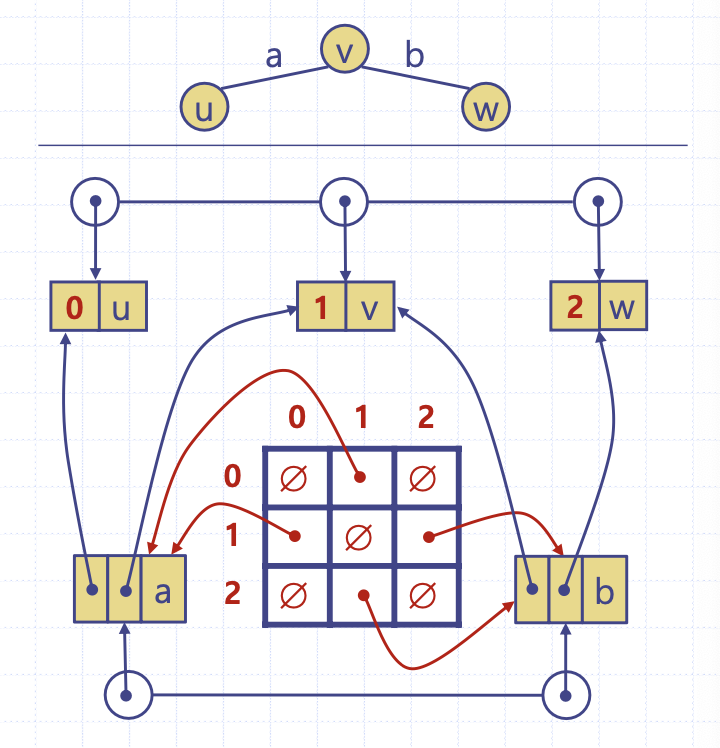
인접행렬 구조도 간선리스트 구조를 개선한 2번째 방법이다.
정점들의 번호를 매기고 매트릭스를 만들어 간선이 있고 없음을 매트릭스에 표기한다. 이 방법에서 정점 v1, v2가 인접한지를 알아내는데 상수 시간밖에 걸리지 않고, 한 정점에 인접한 정점들을 찾는 데 O(n) 시간이 걸린다.
만약 매트릭스 상에서 간선이 있고 없음을 0, 1로 표현하게 되면 간선의 가중치를 담기에 부족하다.
배열을 이용한 그래프 구현
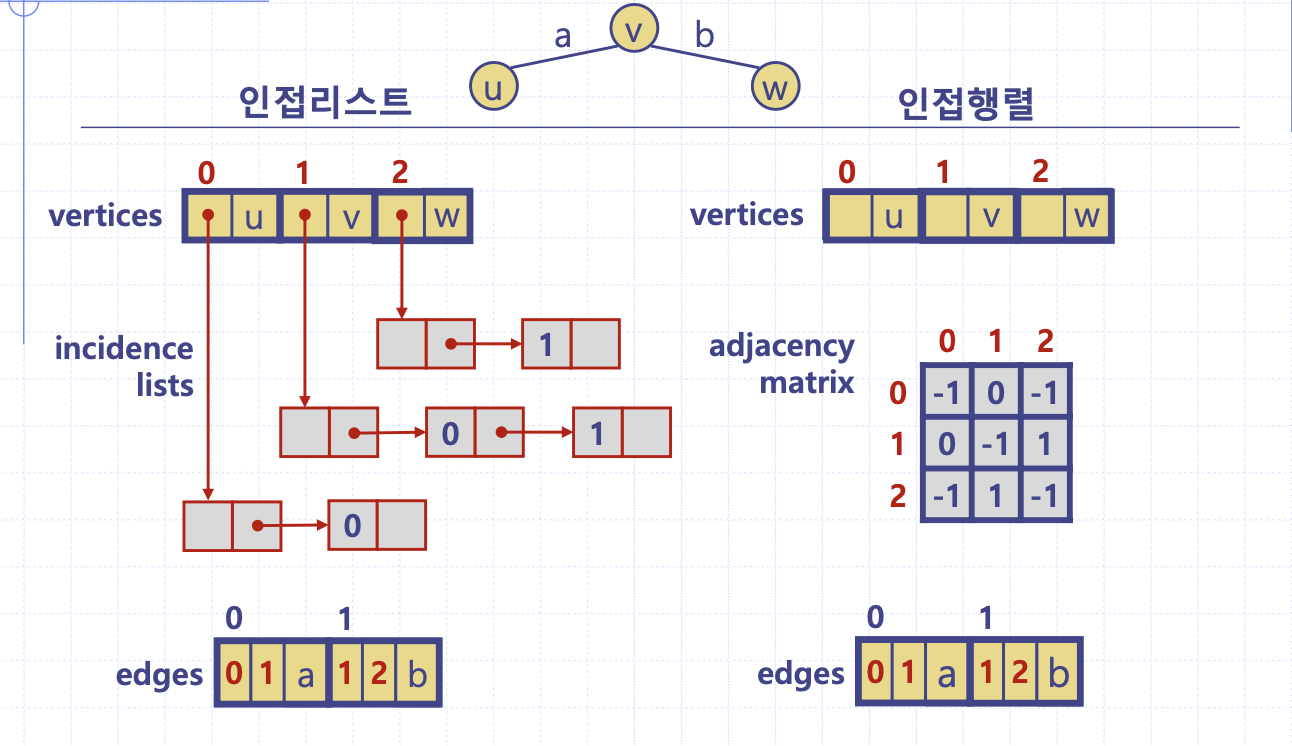
정점 배열과 간선 배열은 구조체 배열이다. 인접리스트의 경우는 연결리스트로 표현하지만, 인접행렬은 2차원 정수 배열을 만든다. 그림의 예시에서 -1은 간선이 없는 초기값이겠고 0은 0번 인덱스의 간선, 1은 1번 인덱스의 간선이 존재함을 표현하고 있다.
인접리스트 vs 인접행렬
전반적으로 인접리스트는 다소 복잡하지만 동적 그래프에 유리하고 그 반대로 인접행렬은 동적 그래프에 불리하지만 배열을 사용해 인접 정보를 쓰기 때문에 구조가 단순하다는 장점이 있다.
구현별 성능
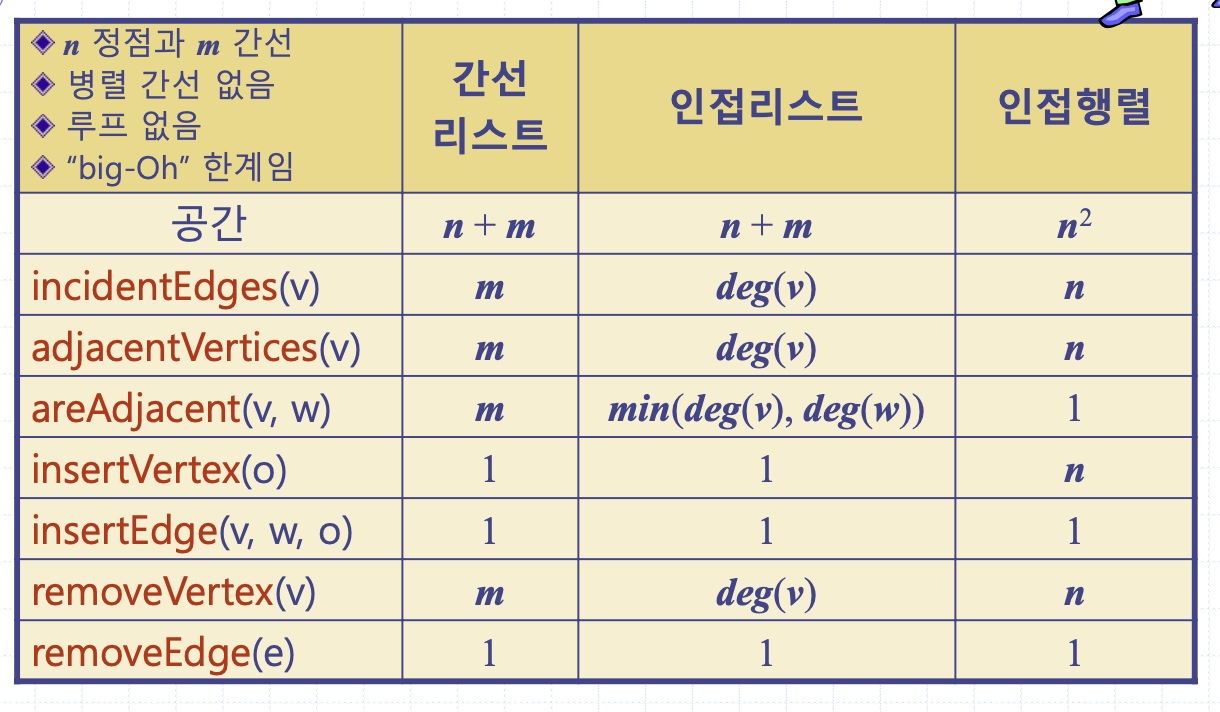
간선리스트가 인접 정보를 탐색할 때, 더 많은 시간을 쓰고 있다. 그렇지만, 인접 정보를 쓰지 않는 문제라면 간선리스트 구조를 채택할 수 있다.
참고 : 국형준. 알고리즘 원리와 응용. 21세기사, 2018.
