
최단 경로 알고리즘은 두 개의 정점에 대한 최소 가중치 경로를 구하는 것이다. mst는 최단 경로와 달리 모든 정점을 취하고 그래프 전체의 간선 가중치가 최소인 것이 차이점이다. 또한, 최단 경로는 digraph에서도 정의할 수 있고 음의 값 간선 가중치에 대해 최단 경로는 부정한다. 음수가 있으면 그로 인한 싸이클이 발생할 수 있게 되어 경로를 찾을 수 없기 때문이다. 또한 mst와 달리 최단 경로는 한 간선을 여러 번 카운트하게 되는 것도 차이점이다.
최단 경로
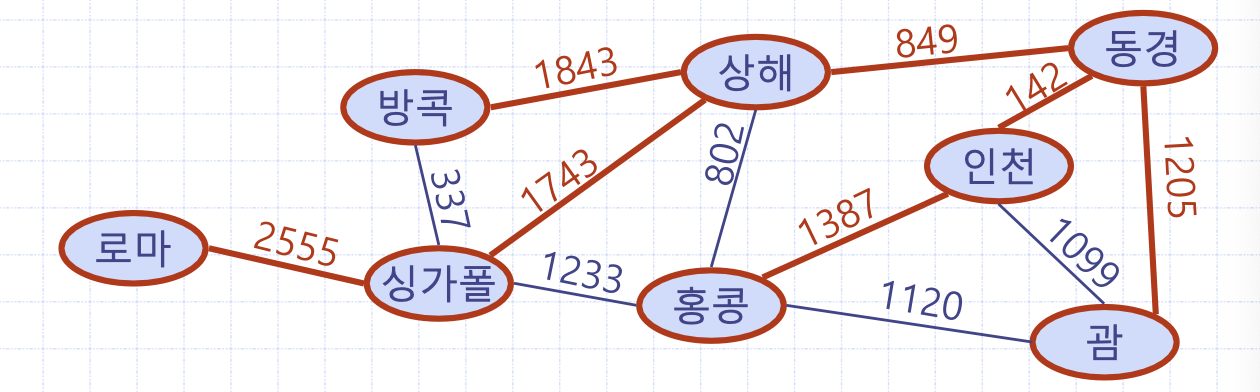
로마-동경의 최단 경로를 구한다고 하자. 그림과 같이 최단 경로를 구했을 때, 경로의 부분 경로 역시 최단 경로가 된다. 예를 들어 홍콩-인천의 최단 경로도 같이 구할 수가 있다.
최단 경로는 어떠한 출발 정점이 주어진 후, 목표 정점까지의 최단 경로를 구하게 된다. 이 때 출발 정점에서 목표 정점이 아닌 다른 모든 정점에 이르는 최단 경로들이 트리의 형태로 존재하게 된다. 이를 단일점 최단 경로라고 하는데, 출발 정점을 동경이라고 했을 때, 그래프 내 모든 정점까지의 최단 경로도 같이 구하게 된다.
최단 경로 포스팅에서 다익스트라, 벨만포드, DAG 알고리즘을 학습한다. 각 알고리즘이 어떠한 상황에서 쓰이고 시간복잡도는 어떻게 다른지를 마지막에 비교하며 정리해보려 한다.
Dijkstra 알고리즘
먼저 다익스트라 알고리즘은 음의 가중치가 없는 무방향 연결 그래프에서 쓰인다. 생각해보면 최단 경로를 구하는 데에 있어서 가장 일반적인 형태에서 쓰인다고 할 수 있겠다.
다익스트라 알고리즘은 mst를 구하는 프림 알고리즘과 거의 동일하다. start 정점을 시작으로 모든 정점들을 하나의 Sack()에 담아간다. 각 정점들에 대해 라벨값을 사용하는데 이는 배낭과 인접 정점들과의 거리를 표현한다.
Alg DijkstraShortestPath(s)
input graph G, start vertex s
output label distance(v), is the distance from s to v
for each v in G.vertex() {
distance(v) <- big number
}
distance(s) <- 0
Q <- priority queue containing all vertices using distance as key
while(!Q.isEmpty()) {
v <- Q.remove()
for each e in G.incidentEdge(v) {
target <- G.opposite(u, e)
if(target in Q) {
if(distance(target) > distance(v) + weight(v, target)) {
// 간선 완화
distance(target) <- distance(v) + weight(v, target)
// 큐 재정렬
Q.replaceKey(target, distance(target))
}
}
}
}프림 알고리즘처럼 모든 정점의 거리 정보를 초기화 하고 Q에 삽입 후 하나씩 꺼내면서 작업한다.
각 반복 라운드는 Q에 빠져나온 정점 v에 대한 부착 간선을 돌며 인접 정점 target을 뽑아낸다. 만약 정점 target이 Q에 존재하고, target에 라벨값이 부착 간선 e의 가중치와 정점 v 라벨값의 합보다 크다면 target의 라벨값을 갱신해주며 간선 완화 작업을 한다.
간선 완화
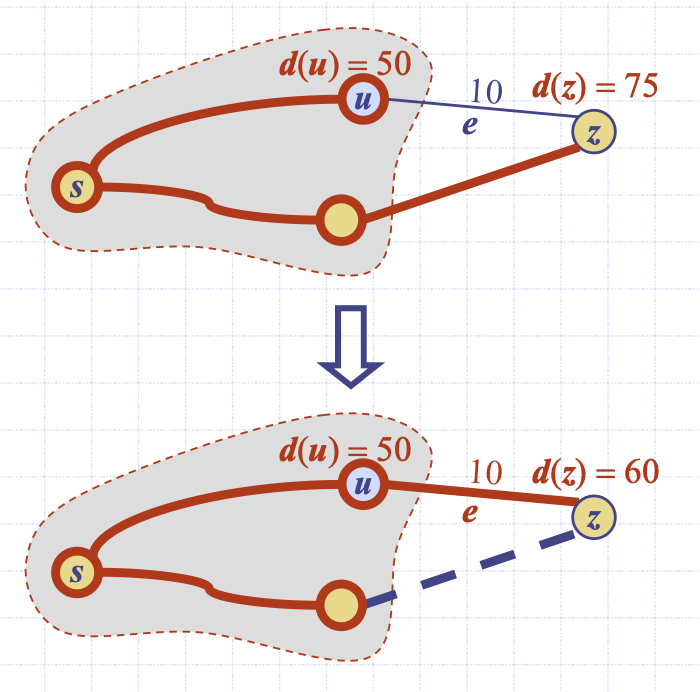
그림 예제로 다익스트라 알고리즘 이해를 돕자.
그림 수행 예시
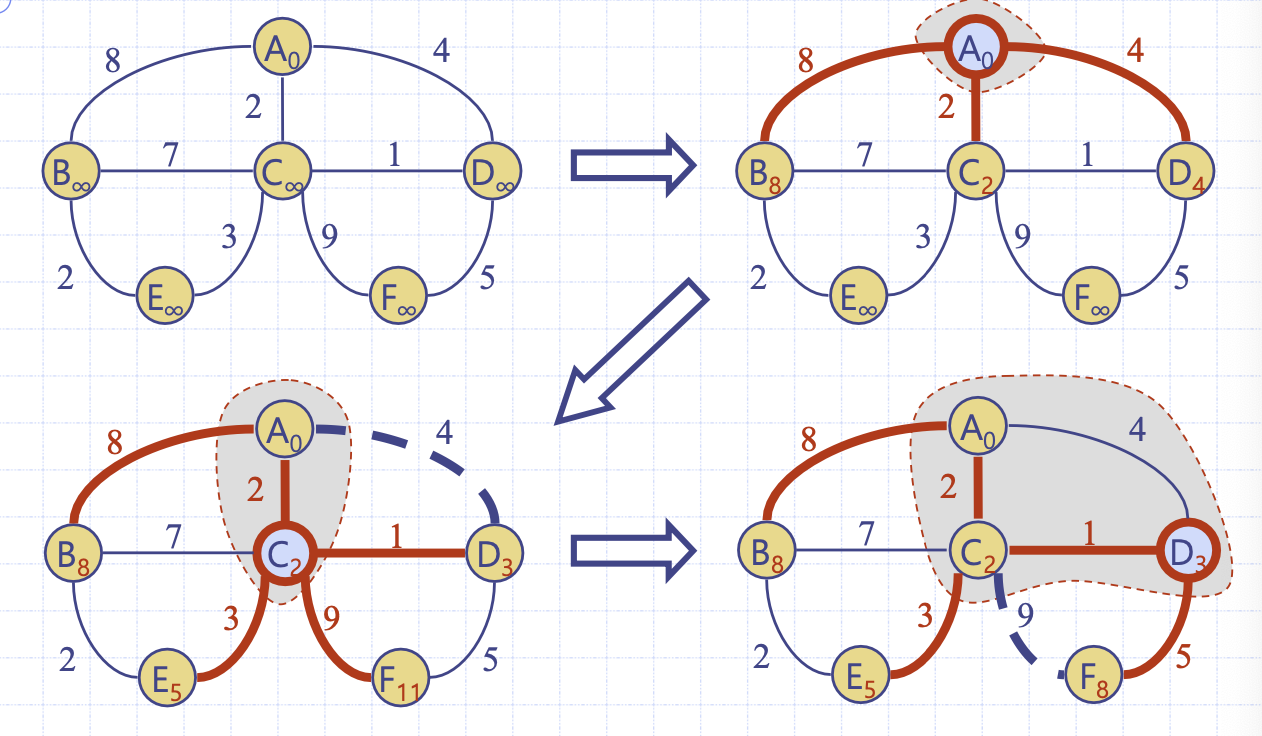
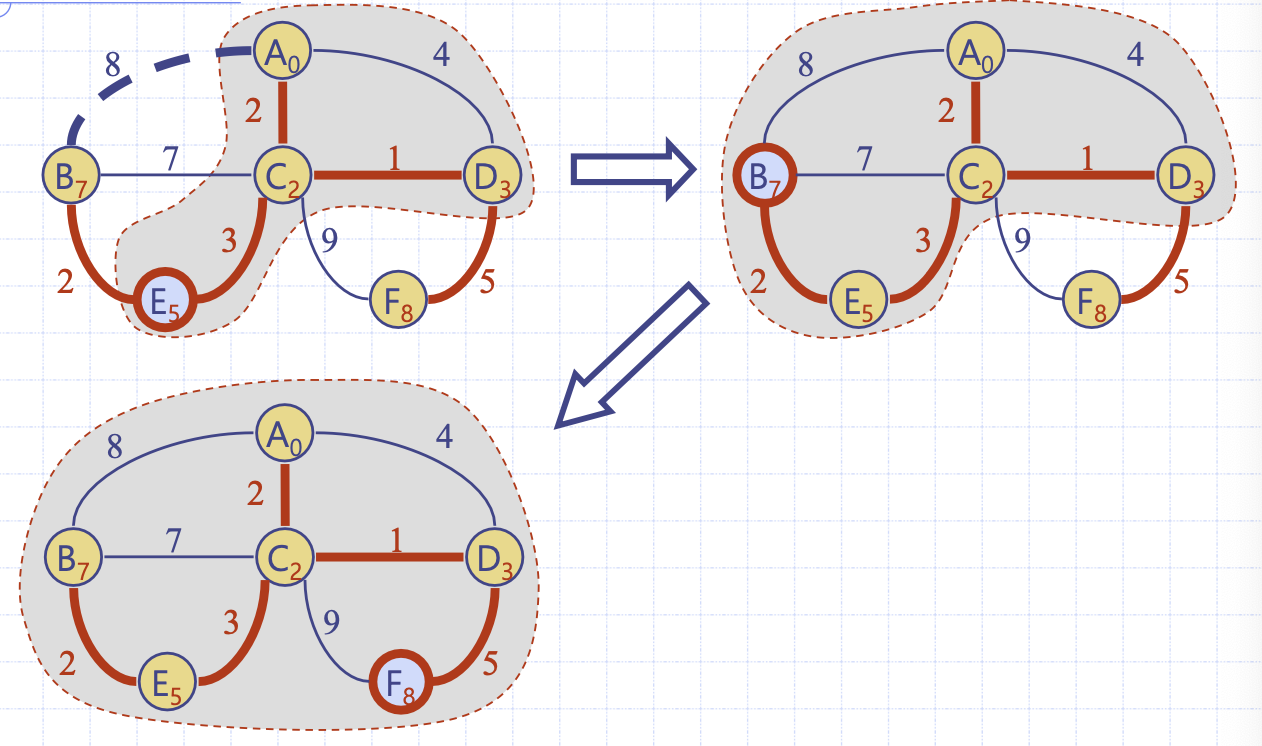
start를 A라 하자. A에 대한 인접 정점 정보를 모두 갱신한다.
A 이후 Q에서 정점을 추출할 때 라벨값이 가장 작은 C가 나올 것이다. C를 Sack()에 담고 C에 대한 모든 인접 정점 정보를 갱신한다. 이런 흐름으로 모든 정점에 대해 반복하면 그래프의 최단 경로를 구할 수 있다.
최종 완성된 그림에서 각 정점의 라벨을 보자. 라벨의 정보는 출발 정점(A)로부터의 최단 경로를 의미하게 된다. A의 라벨값 0은 A에서 A로의 경로, F의 라벨값 8은 A에서 F로의 경로다.
다익스트라 알고리즘, 음의 가중치
다익스트라 알고리즘은 탐욕법에 기초한다. 그 때 그 때 가장 경로값이 작은 순서대로 정점을 취하기 때문이다.
이 때, 음의 가중치가 있다면 어떻게 될까? 그림 예시의 3번째 순서를 보자. A와 C는 배낭에 들어가게 된다. 이는 A부터 C까지의 최단 경로는 확정되었음을 의미하는데 만약 이후 간선에 음수가 있다면 이러한 경로 확정이 무산된다.
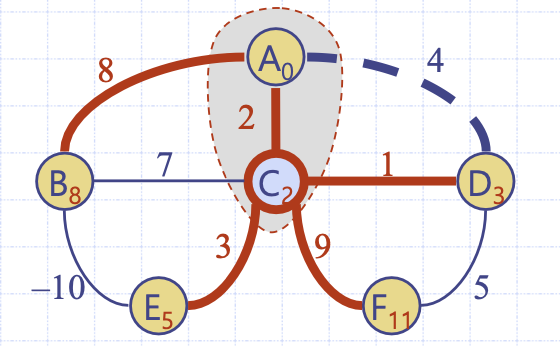
A->C는 2이지만, (B, E)로 인해 A->B->E->C가 최소 경로가 되기 때문이다.
다익스트라 알고리즘 성능
우선순위 큐
우선순위 큐가 힙이라면,
각 정점들은 한 번 삽입, 삭제 된다. -> O(Vlog V)
우선순위 큐 내의 정점 라벨값들은 최악의 경우 본인의 degree만큼 갱신된다. 갱신된다면 그에 따른 큐의 재정렬도 해야한다. -> O(Elog V)
결론적으로 O((V+E)log V) 시간복잡도를 가진다. 만약 연결 그래프라면 V는 E보다 작기 때문에 O(Elog V)로 표현할 수 있다.
무순리스트 큐
큐가 만약 우선순위 큐가 아닌 무순리스트라면,
삽입에 대해 O(1), 삭제에 대해서는 O(V)이다. -> O(V^2)
큐의 정점 라벨값들은 본인의 degree만큼 갱신될 수 있으며 각 소요 시간은 O(1)이다. -> O(E)
무순리스트에서 다익스트라 알고리즘은 O(V^2 + E) 시간복잡도를 가진다.
그래프의 밀집도에 따라서...
우선순위 큐를 사용하는 다익스트라 알고리즘은 O(Elog V) 시간 걸린다.
그래프가 밀집되어 간선 수 E가 V의 제곱에 가깝다고 하면, 각 정점의 degree는 V가 되어 간선 완화에 따른 큐의 재정렬에 대한 비용이 O(V^2log V)까지 올라간다. 다익스트라 알고리즘은 관리되는 간선이 적은, 밀집도가 낮은 그래프에 유리한 전략이다. 이는 mst의 프림 알고리즘도 마찬가지다.
참고: 국형준. 알고리즘 원리와 응용. 21세기사, 2018.
