이번 포스팅은 다익스트라 알고리즘에 이어서 벨만포드 알고리즘으로 그래프 내 최단 경로를 찾는 방법을 배운다.
벨만포드 알고리즘은 다익스트라와 달리 음의 가중치를 허용하고 양방향이 아닌 방향 간선을 전제한다. 총 V-1회의 반복 라운드를 거치고 각 라운드에서 그래프 내 모든 간선에 대해 간선 완화를 시도한다.
벨만포드 알고리즘 의사코드
Alg BellmanFordShortestPath(s)
input start vertex s
output label distance(v), is the distance from s to v
for each v in G.vertex() { //모든 정점 거리 초기화
distance(v) <- big number
}
distance(s) <- 0 //시작 정점 거리 0
for i<-1 to n-1 { //V-1회 반복
for each e in G.edge() { //모든 간선에 대한 dest 거리값 갱신
start <- G.origin(e)
dest <- G.opposite(start, e)
distance(dest) <- min(distance(dest), distance(start) + weight(e))
}
}벨만포드는 V-1회 반복마다 모든 정점에 대한 도착 정점 distance 값을 갱신한다.
왜 V-1회 반복일까? 지하철 노선도를 떠올려 보자. 출발역에서 도착역이 일렬로 쭈르르 간다고 하고 출발역과 도착역까지는 V개의 지하철역이 있다고 했을 때, 지하철 노선은 V-1개다.
벨만포드의 핵심은 i번째 반복 라운드에서 출발역으로부터 i개의 간선을 사용하는 최단 경로를 찾는 것이다. 따라서 최대의 경우를 고려하여 V-1까지 보는 것이다.
벨만포드 알고리즘 그림 수행 예시
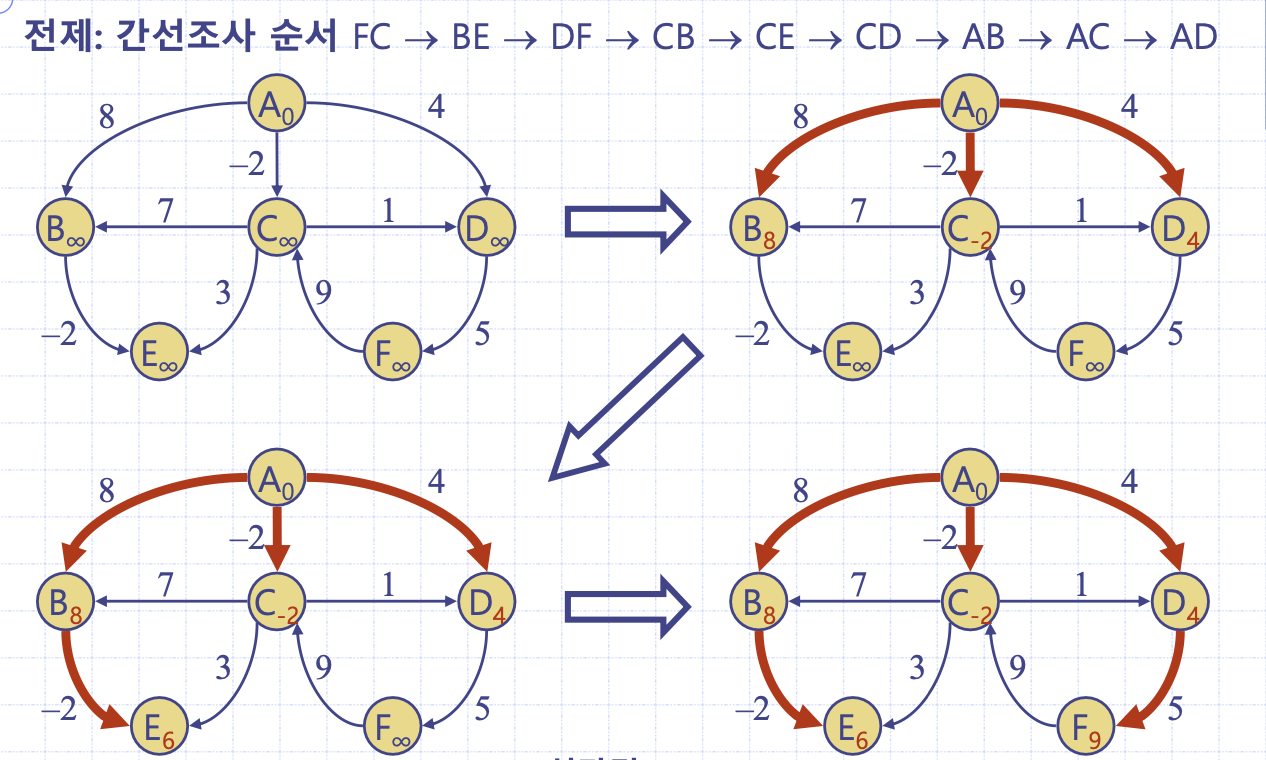
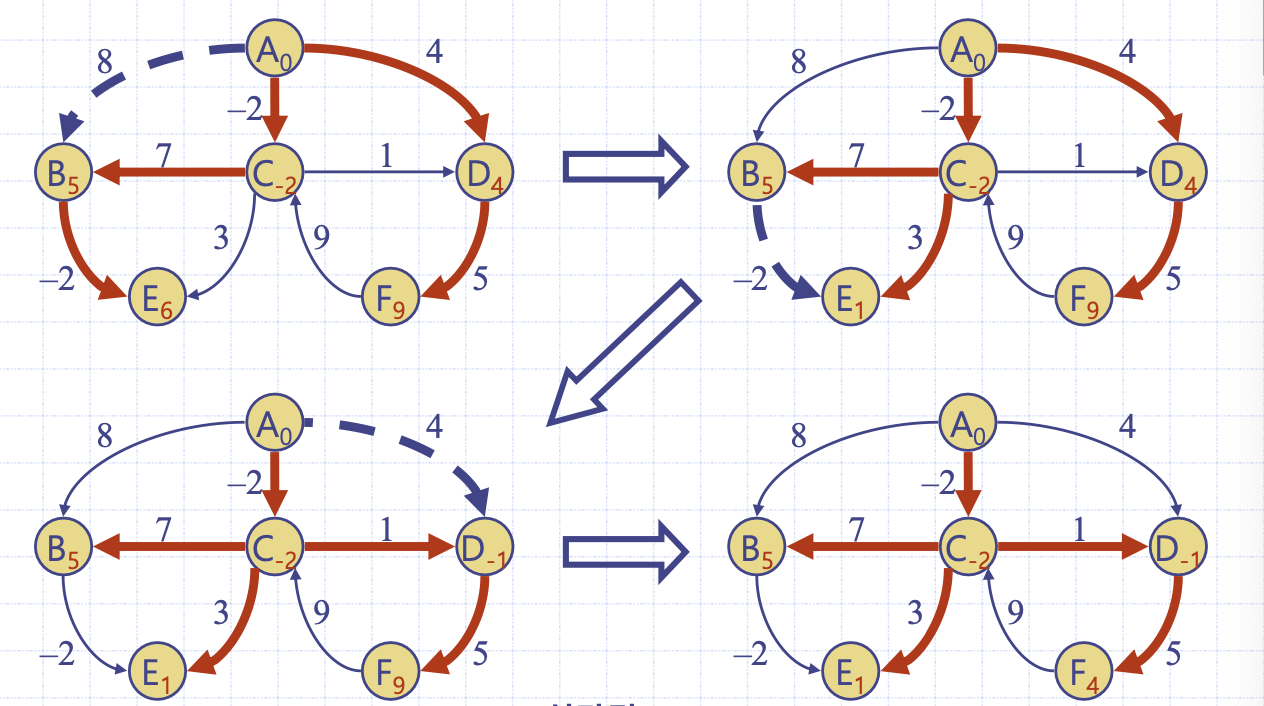
벨만포드 알고리즘에서 전체 간선 조사 순서는 다음과 같고 출발 정점은 A라 가정하자.
1 라운드에서 간선 조사 순서를 쭉 돌며 B, C, D에 대한 간선 완화 작업을 할 수 있다. (E, F의 경우 무한대에서 정수를 더하거나 빼준다 해도 무한대다.)
2 라운드에서는 모든 정점 라벨값을 갱신할 수 있다. E를 보면 무한대에서 B를 거쳐 E로 오는 distance가 6이므로 갱신된다.
벨만포드 알고리즘은 다익스트라 알고리즘과 달리 확정된 경로가 존재하지 않고 새로운 경로가 계속해서 생길 가능성이 있기 때문에 모든 간선을 V-1회 조사한다.
벨만포드 알고리즘은 O(VE)다. O((V+E)log V)인 다익스트라 알고리즘에 비해 시간복잡도는 크지만, 음수 가중치에 대한 최단 경로를 계산할 수 있다는 장점이 있다.
