Algorithm - 4. Heap Sort

저번 포스트의 힙 자료구조에 이어 힙을 이용한 정렬 알고리즘을 알아보자.

---

힙 정렬

Alg heapSort(L)
	input list L
    output sorted list L

H <- empty heap
while(!L.isEmpty()){
	k <- L.removeFirst()
    H.insert(k)
}
while(!H.isEmpty()){
	k <- H.remove()
    L.addLast(k)
}
return

위는 힙 정렬 의사 코드다. 힙 정렬 알고리즘은 무순의 리스트를 정렬하는 것을 목표로 한다.

먼저 heap을 생성해준다. O(1)

(1번째 while) 리스트가 비어질 때까지 원소를 뺀다. O(1)을 N번. O(N).
힙에 원소를 집어 넣는다. O(logN)을 N번. O(N logN).

(2번째 while) 힙이 비어질 때까지 힙의 원소를 뺀다. remove작업 O(logN) N번. O(N logN).
리스트에 원소를 넣는다. O(1)을 N번. O(N).

따라서, N개에 원소에 대해 O(N logN) 시간에 리스트를 정렬할 수가 있다.

---

힙 정렬 개선

그러나 현재의 힙 정렬을 공간적으로, 시간적으로 개선할 수 있는 방법이 있다.

제자리 힙 정렬(공간)

L을 정렬하기 위해 H이라는 외부 공간을 마련해 정렬을 하는 것이 아닌 L 자체에서 일부를 힙 공간으로 마련해 정렬하는 것을 말한다.

제자리 힙 정렬은 배열에서만 적용한다. 또한, 오름차순 정렬을 위해서는 최대힙을 사용하는 것도 여태와의 차이점이다. 왜 최대힙을 사용하는지는 뒤에서 확인하자.

다음은 제자리 힙 정렬의 의사 코드다.

Alg inPlaceHeapSort(A)
	input array A of n keys
    output sorted array A

buildHeap(A)
for i <- n downto 2{
	A[1] <-> A[i]
    downHeap(1, i-1)
}
return

ALg buildHeap(A)
	input array A of n keys
    output heap A of size n

for i <- 1 to n{
	insert(A[i])
}
return

buildHeap()은 input 배열로부터 Heap을 만드는 것이다. 수행 시간은 O(N logN)이다.

힙이 생성이 되면 idx n부터 2까지 내려가면서 반복문을 탄다. 힙의 1번째 원소와 idx원소를 교환하고 1번째 원소부터 idx의 바로 앞 부분까지 downHeap()을 수행한다.

이 지점이 바로 최대힙으로 구현하는 이유다. 최대힙이기 때문에 가장 큰 원소가 가장 앞에 올 것이고, 가장 큰 원소는 idx와 스왑이 되며 스왑 이후에는 스왑된 부분 바로 앞까지 downHeap() 하여 스왑된 부분 앞까지는 힙 속성을 유지해 나가면서 외부 공간을 사용하지 않고 힙 정렬이 이루어지기 때문이다.

downHeap()의 의사코드를 보자.

Alg downHeap(i, last)
	input index i, last of array A
    output none

left <- 2i
right <- 2i+1
if(left > last){
	return
}

bigIdx <- left						//bigIdx찾기
if(right <= last){
	if(key(A[right]) > key(A[bigIdx])){
		bigIdx <- right
    }
}
if(key(A[i]) >= key(A[bigIdx])){	//힙 속성이 충족함
	return
}
A[i] <-> A[bigIdx]					//힙 속성이 위배됨
downHeap(bigIdx, last)

left와 right 중 더 큰 원소를 가리키는 원소를 골라낸 후 파라미터로 전달된 i와 비교를 한다. 만약 힙 속성이 위배되면 두 원소를 swap해주고 downHeap()을 호출한다. 이 때 i에는 left와 right 중 더 큰 원소를 가리키는 인덱스를 전달한다.

그림 예시

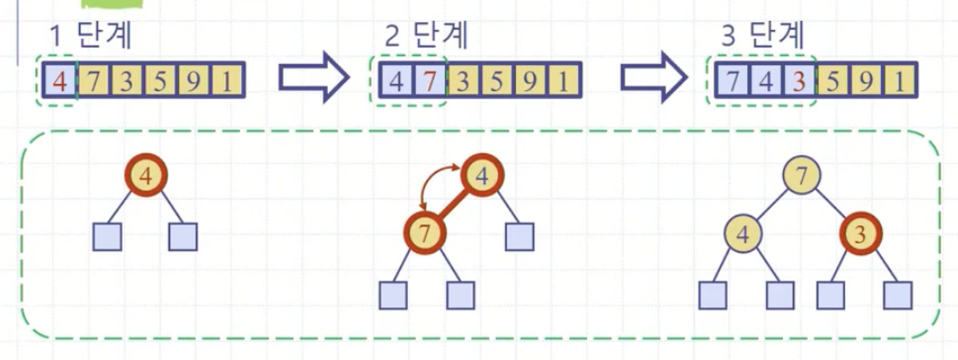
{4 7 3 5 9 1} 의 배열이 있다. 여기서 먼저 할 일은 buildHeap()을 통해 해당 배열을 최대힙으로 만들어주는 것이다. 물론 인덱스는 1부터 시작한다.

배열의 인덱스 순서대로 원소를 차곡차곡 insert한다. 물론 이 과정에서 upHeap()이 일어난다.

buildHeap()에서 반복문의 인덱스가 3에 와 있다면, 1~3까지는 힙으로 되어 있을 것이고 4~6까지는 아직 초기 배열 상태 그대로일 것이다.

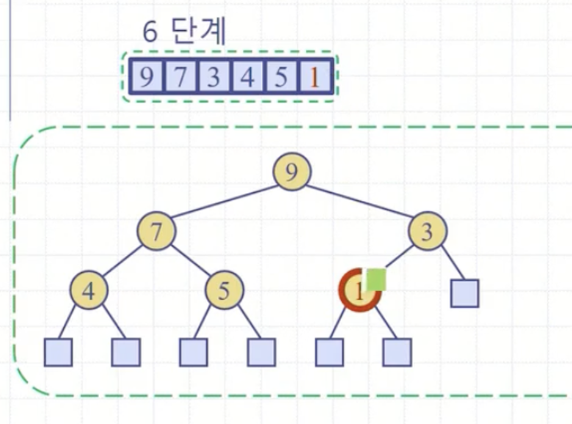
끝 인덱스까지 insert작업을 마치면 배열 전체가 힙으로 바뀐다.

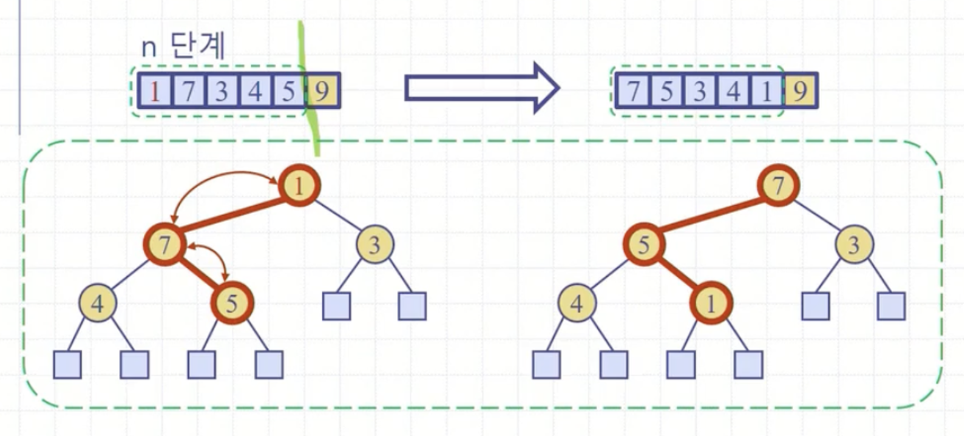
이제 힙을 가지고 정렬을 한다. 최대 힙이기에 가장 큰 원소는 1번째에 위치한다. 마지막 인덱스와 바꿔준다.

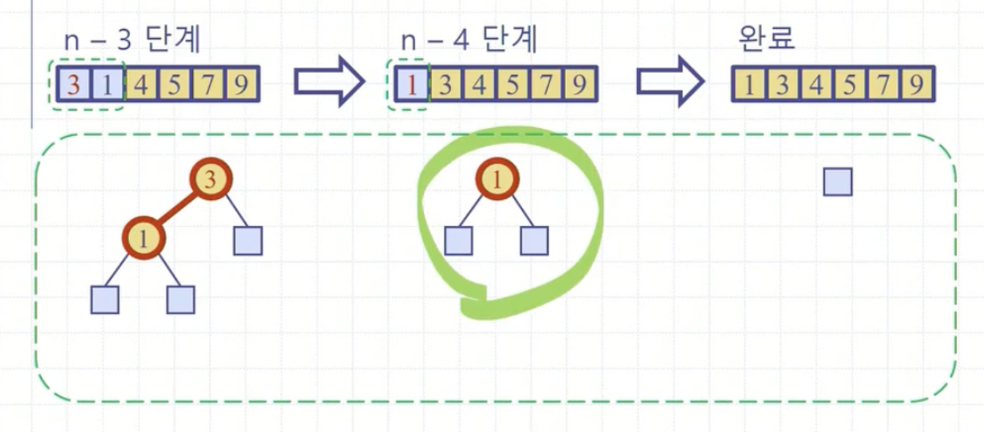
이렇게 계속 힙의 1번째 원소를 뒤로 빼주면서 작업을 하면 전체 배열이 정렬이 된 채로 완성된다.

상향식 힙생성(시간)

여태까지의 방법에서는 힙 생성을 insert 작업(O(logN))을 N번 하여 O(N logN)에 했다. 만약 힙에 저장되어야 할 모든 key들이 미리 주어질 경우, O(N) 시간으로 단축할 수 있다.

재귀

Alg rBuildHeap(v)
	input node v
    output heap with root v

if(!isExternal(v)){
	rBuildHeap(left(v))
    rBuildHeap(right(v))
    downHeap(v)
}

의사 코드는 node라고 표현을 했다. 힙을 리스트로 구현된 완전이진트리라고 보고 있는데 배열로 구현하는 것 자체가 힙을 완전이진트리라고 보고 있는 것이기도 하다. node v 대신에 배열의 idx를 전달한다고 생각을 해도 무방하다. 최초의 인덱스 전달은 1이 될 것이다. 조건문으로 들어가 현재 인덱스로의 배열 접근이 유효하다면, rBuildHeap(2i), rBuildHeap(2i+1)을 전달하고 수행을 마치면 downHeap()을 한다.

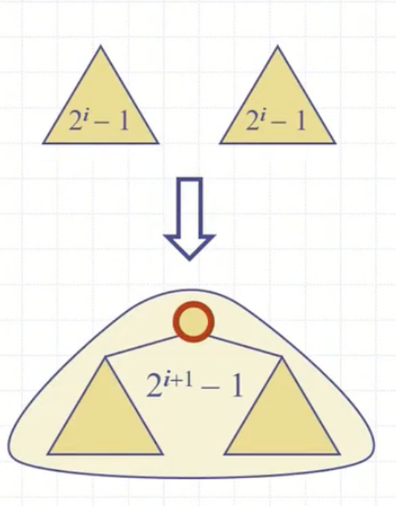
사실 이 개념은 트리들을 위로 점차 묶어가면서 전체적으로 힙을 생성해간다고 생각하면 이해가 쉽다.

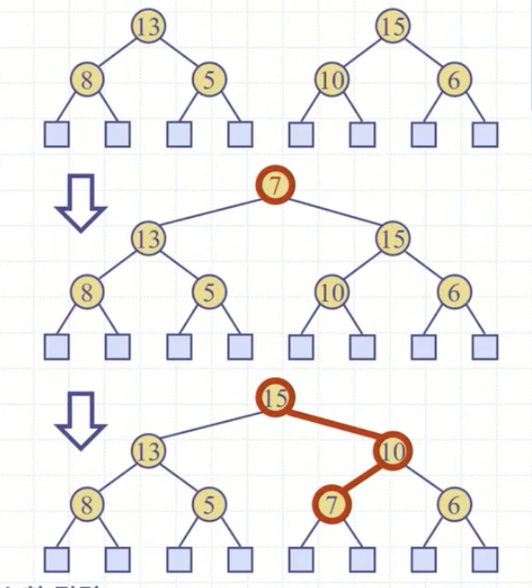
비재귀

비재귀적으로도 상향식 힙생성이 가능하다.

Alg buildHeap(A)
	input array A of n keys
    output heap A

for i <- n/2 downto 1
	downHeap(i, n)	//i부터 n 인덱스까지 downHeap을 한다는 것

제법 단순한데 의문인 점은 idx가 n/2부터 시작해 1까지 내려가며 downHeap()을 한다는 것이다. 왜 n/2부터 시작하는 것인가?

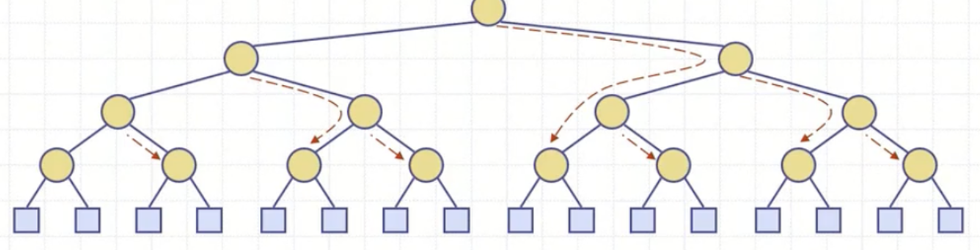
힙은 완전이진트리이다. n부터 n/2는 depth가 1인 각각의 단독 노드일 것인데 이들은 downHeap() 작업이 필요가 없기 때문이다. 만약 depth 1의 노드 중 일부가 비어있어도 n/2부터 시작을 해도 되는 것일까?

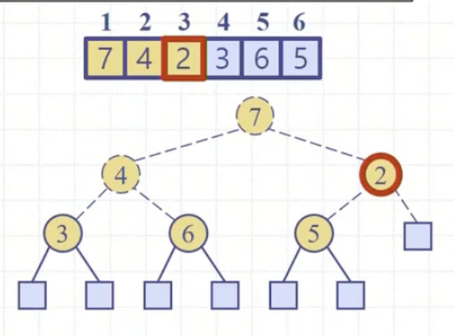
전체 6개의 노드들이 있고 비재귀 상향식을 하게 되면 인덱스는 3부터 1까지 가면서 downHeap(3, 6) -> downHeap(2, 6) -> downHeap(1, 6) 을 호출하게 될 것이다.

성능

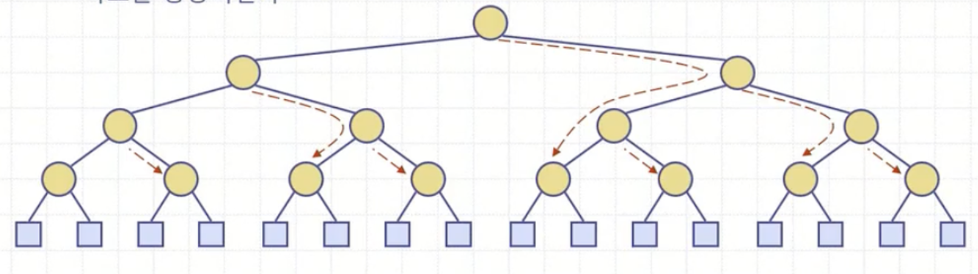
상향식 힙생성의 성능은 downHeap()을 전체 몇 번 시도하냐에 따른 노드 방문 횟수가 결정할 것인데, 그림과 같이 최악의 경우로 노드를 방문하더라도 O(N)개 방문한다. 따라서, 상향식 힙생성은 빅-오메가(N)에 수행된다. 하지만 어디까지나 힙생성을 개선한 것이지, 힙 정렬에서는 여전히 O(N logN)이다. 그러므로 힙생성-힙 정렬로 이어지는 힙 정렬 전체 과정의 시간복잡도는 O(N logN)이다.

그렇지만 상향식 힙생성은 원소 하나하나 삽입하면서 생성하는 삽입식 힙생성의 방식보다는 속도를 향상시킨다는 것에 의의가 있다.

---

참고 : 국형준. 알고리즘 원리와 응용. 21세기사, 2018.