Algorithm - 6. Quick Sort

Mingi Shin·2023년 10월 21일

목록 보기

6/23

퀵 정렬은 합병 정렬과 마찬가지로 분할정복에 기초한 정렬 알고리즘이다. 이 역시 어떠한 리스트를 2개로 쪼갠 후 정렬하고 합치는 작업을 거친다.

다만, 퀵 정렬은 합병 정렬과 달리 pivot이라는 기준점을 사용해 partition한다.

합병 정렬은 conquer(정복) 단계에서 많은 시간을 투자하지만, 퀵 정렬은 divide(분할) 단계에서 시간이 많이 걸린다. 그만큼 pivot을 활용한 partition 작업이 굉장히 중요한 부분이라고 할 수 있다.

퀵 정렬

ALg quickSort(L)
	input list L
    output sorted list L
    
if(L.size() > 1){
	pivotIdx <- a position in L
    LT, EQ, GT <- partition(L, pivotIdx)
    quickSort(LT)
    quickSort(GT)
    L <- merge(LT, EQ, GT)
}
return

퀵 정렬 알고리즘은 무순의 리스트를 정렬하여 리턴하는 것을 목표로 한다.

퀵 정렬은 파라미터 리스트의 사이즈가 1보다 클 때까지 재귀적으로 반복한다. 합병 정렬과 매우 유사하다. 먼저 pivotIdx를 리스트 안에서 추출한다. 난수를 돌려서 뽑는 방법도 있고 마지막 인덱스를 pivot의 idx로 설정하는 경우도 있다. 조금의 최적화를 위해 인덱스를 3개 뽑아 그 중 중간값을 가리키는 인덱스를 pivotIdx로 설정할 수도 있다.

partition함수는 pivot을 기준으로 LT, EQ, GT 3가지 리스트로 나눈다. LT는 pivot보다 작은 원소들을 모아 놓는다. EQ는 pivot과 같은 값을 모아 놓는다. GT는 pivot보다 큰 원소들을 모아 놓는다.

이후 LT와 GT를 재귀 호출하고 리턴되어 돌아오면 3개의 리스트를 merge한다.

분할(partition)

Alg partition(L, k)
	input list L, pivotIdx k
    output LT, EQ, GT

pivot <- L.get(k)	//피봇 저장
LT, EQ, GT <- empty list
while(!L.isEmpty()){
	elem <- L.removeFirst()
    if(elem < pivot){
    	LT.add(e)
    } else if(elem > pivot){
    	GT.add(e)
    } else{
    	EQ.add(e)
    }
}
return LT, EQ, GT

partition()은 pivot의 인덱스와 리스트를 입력 받아 LT, EQ, GT 3가지 리스트를 반환한다. 리스트의 원소가 비어질 때까지 원소를 하나씩 빼서 pivot과 비교해 적절한 리스트에 저장해 반환하는 알고리즘이다.

리스트의 삽입이나 삭제는 O(1)에 수행되지만 N개의 원소를 훑기 때문에 전체 O(N)에 수행된다.

그림 예시

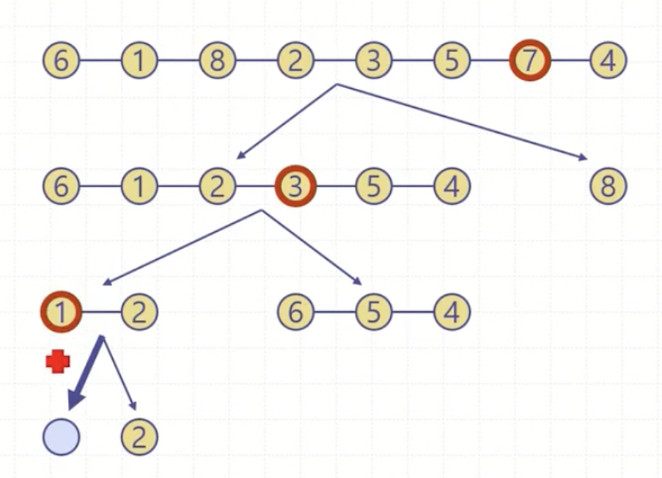
수행 시간

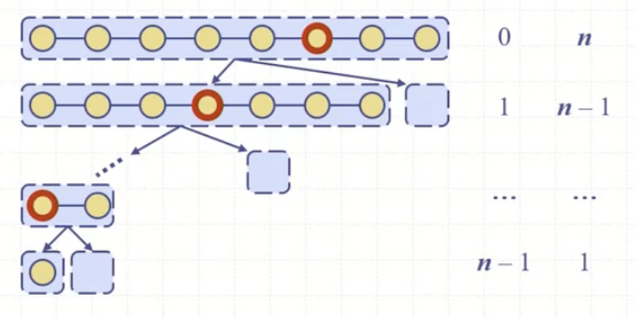
최악의 시나리오에서 퀵 정렬은 O(N^2) 시간이 걸린다. 피봇을 계속해서 잘못 선택하여(input list의 최솟값이나 최댓값만 선택하는) partition의 결과가 N-1과 1개의 리스트로 나누어진다면 N + N-1 + ... + 2 + 1 이 되어 N(N-1)/2 즉, O(N^2)이 된다.

기대 실행 시간

하지만 실제로 퀵 정렬이 O(N^2)에 수행될 경우는 만무하고 좋은 호출과 나쁜 호출을 반복하면서 partition() 작업을 할 것이다.

우리는 여기서 좋은 호출과 나쁜 호출의 확률을 각각 1/2로 하여 기대 실행 시간을 구할 수 있다. 좋은 호출과 나쁜 호출은 무엇일까?

partition을 했을 때, LT와 GT가 적어도 input list의 3/4보다 작은 경우 골고루 나누어졌다 판단하여 좋은 호출이라 가정하고 그 이외를 나쁜 호출이라 가정한다.

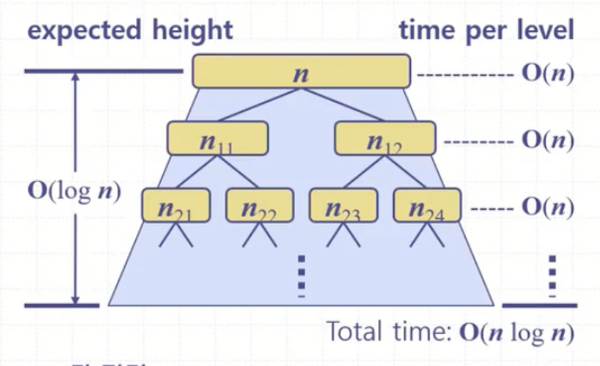
좋은 호출은 leftList의 size를 3/4N으로, rightList의 size를 1/4N으로 한다 가정한다. 깊이가 i까지 내려갈 때, i/2는 좋은 호출이다. 따라서 리스트의 최대 크기는 (3/4)^(i/2) N(3/4 ^ 좋은 호출 개수 리스트 크기)이다.

(3/4)^(i/2) * N = 1을 기대하는 것이고, 깊이 i에 대한 값을 구해보면 2 log(3/4)N이 되어 퀵 정렬 기대 높이는 결국 O(log N)이 된다.

각 높이에 대한 partition() 수행은 O(N)으로 일정하기 때문에 결국 퀵 정렬 트리의 높이가 얼마느냐에 따라 실행 시간이 달린 것이고 O(N logN)이 퀵 정렬의 기대 실행 시간이 된다. 사실 깊이는 logN보다 깊게 내려가겠지만, 어찌되었든 빅-오로 봤을 떄 logN이 된다.

제자리 퀵 정렬

퀵 정렬은 배열로 구현하여 제자리에서 수행했을 때 그 진가가 발휘된다.

Alg inPlaceQuickSort(L, p, r)
	input list L, position p, r
    output sorted list L from p to r

if(p >= r)
	return

pivotIdx <- between p and r		//pivot의 인덱스 설정
a, b <- inPlacePartition(L, p, r, pivotIdx)	//a, b는 EQ의 범위(같을 수 있음)
inPlaceQuickSort(L, p, a-1)	//LT quick sort
inPlaceQuickSort(L, b+1, r)	//GT quick sort
return

주석의 설명대로 피봇을 잡아 놓고 partition을 한다. partition의 리턴값은 a와 b 인덱스인데 이는 a~b까지 pivot과 같은 값이라는 의미다.

크게 달라졌다고 할 수 있는 부분은 리스트의 시작과 끝점을 전달하고 있다는 것이다.

분할(partition)

Alg inPlacePartition(A, p, r, pivotIdx)
	input array A[p...r], index of pivot
    output index a, b that means bound of EQ

pivot <- A[pivotIdx]
A[pivotIdx] <-> A[r]	//피봇이랑 마지막이랑 바꿈
i <- p		//맨 앞
j <- r-1	//pivot 앞

while(i <= j){
	while(i <= j & A[i] <= pivot){
    	i++
    }
    while(i <= j & A[j] >= pivot){
    	j--
    }
    
    if(i < j){
    	A[i] <-> A[j]
    }
}
A[i] <-> A[r]
return i

조금 복잡한 형태인데 실제로는 그렇지 않다. while문에 진입하기 전 사전 작업이 이루어진다. pivot index로 pivot을 설정하고 pivot원소를 배열의 가장 마지막 r과 swap해주며 숨긴다. 그리고 i와 j를 설정하는데 i는 앞에서부터 우측 방향으로 증가하며 진행되고, j는 피봇이 있는 r의 앞부분부터 좌측 방향으로 감소하며 진행된다.

i와 j가 역전되지 않을 때까지 반복문이 수행된다. i는 앞에서부터 pivot보다 작은지를 검사하며 지나간다. 어떤 원소가 pivot보다 크다면 잠깐 멈춘다. j도 마찬가지로 뒤에서부터 훑는데 pivot보다 작은 값을 만나면 멈춘다. i와 j가 멈춘 이유는 그 값이 거기 있을 자리가 아니기 때문이다. 둘을 swap 해주면서 작은 값은 앞으로, 큰 값은 뒤로 서로 보내준다. 쭉쭉 진행이 되다가 i와 j가 역전되면 반복문을 탈출한다.

탈출한 후, 숨겨 놓았던 pivot의 자리를 잡아주어야 한다. 이 때 i와 r을 교환하는데 r자리에 들어갈 원소는 분명 pivot보다 큰 값이어야 한다. i와 j가 역전된 이 시점에서 i는 pivot보다 큰 값을, j는 pivot보다 작은 값을 가리키고 있기 때문에 i와 pivot이 있는 r과 swap을 해주며 partition작업을 마친다.

그림 예시

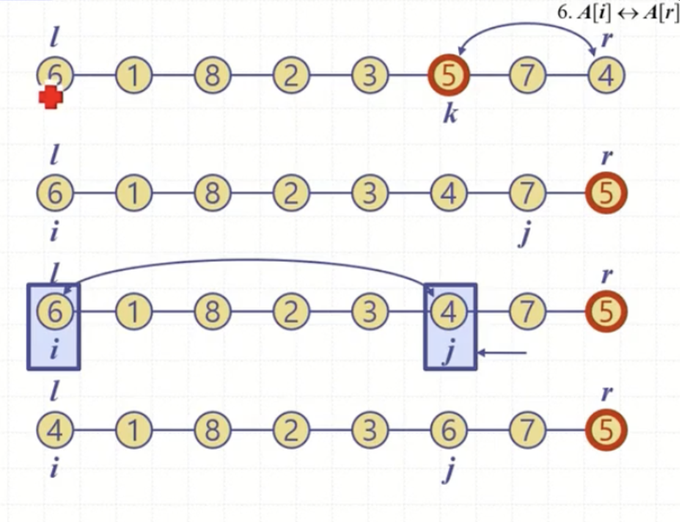
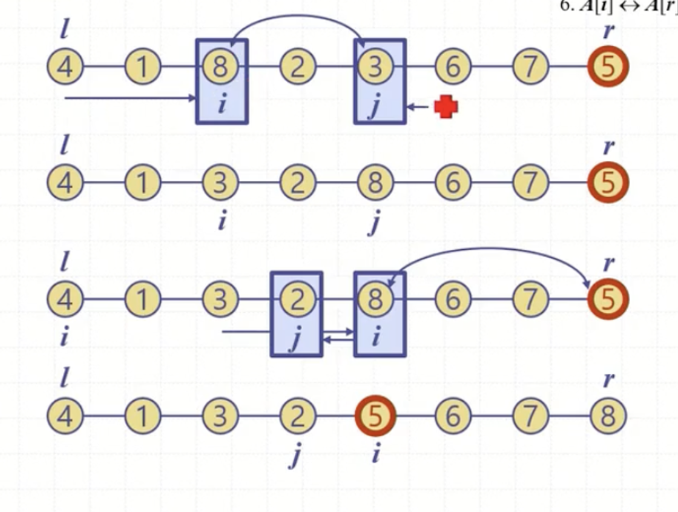
앞선 알고리즘 설명을 그림으로 나타낸 것이다. 피봇 5를 뒤에 숨겨주고 i와 j로 원소들을 검사하며 여러번의 swap을 거친 후 마지막에 i와 pivot의 위치 r을 swap한다.

vs merge sort

두 알고리즘을 4가지 항목에서 공통점과 차이점으로 비교해보자.

	합병 정렬	퀵 정렬
방법	분할 정복	분할 정복
실행 시간	O(N logN)	최악 : O(N^2), 기대 : O(N logN)
partition, merge	partion 쉬움, merge 어려움	partition 어려움, merge 쉬움
작업 순서	small -> big	big -> small