Algorithm - 10. AVL Tree

Mingi Shin·2023년 10월 23일

목록 보기

10/23

탐색 트리로 구현하는 BST의 주요 메서드는 트리의 높이에 메서드의 성능이 좌지우지된다. 포스팅에서 다룰 AVL Tree(자가 균형 BST)도 트리의 높이에 따라 탐색, 삽입, 삭제의 성능이 결정되는 것은 마찬가지다. 이름에서 알 수 있듯이 BST와의 차이점은 트리의 높이를 균형있게 쌓아 올려 메서드 수행을 O(logN)에 할 수 있게 하는 것이 목적이다.

AVL 트리 주요 메서드

트리의 모든 내부노드에 대해 자식들의 좌우 높이 차가 1이 넘지 않는 이진탐색트리를 AVL 트리라 한다.

그림 예시로 정의의 이해를 돕자.

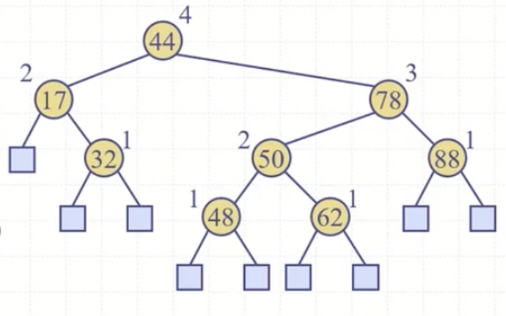
내부노드의 키들이 BST 속성을 유지하면서 존재하고 노드의 주변에 1, 2, 3 같은 정수가 표기되어 있는데 이는 해당 트리 기준으로 높이를 의미한다. 루트는 48, 62까지 최대 내려갈 수 있어 높이가 4고 17은 32까지 내려갈 수 있어 높이가 2다.

루트 노드 44의 좌우 자식들의 높이는 각각 2, 3이다. 특정 노드에 대해 좌우 자식들의 높이 차이가 2이상 차이나지 않기 때문에 그림은 AVL 트리 속성을 준수하고 있다. AVL 트리는 N개 데이터에 대해 O(logN)의 높이를 보장하지만, 노드의 높이 정보를 각각이 저장해야 하는 부담이 존재한다.

AVL 트리는 탐색, 삽입, 삭제에서 BST와 유사하지만, 삽입과 삭제에 대한 추가 작업을 요구한다. 예를 들어 그림에서 '49'의 원소가 삽입되었다면 트리의 높이 균형이 깨진다. 따라서 삽입과 삭제 후에 불균형을 검사하고 fix하는 작업을 통해 트리의 균형을 회복하는 작업이 필요하다.

탐색

먼저 탐색 메서드를 살펴보자. 탐색의 경우는 BST와 같은 로직으로 부담이 덜하다.

Alg searchAVL(node, k)
	input node, key k
    output node with key k or externalNode

if(isExternal(node))
	return node

while(!isExternal(node)){
	if(key(node) = k){
    	return node
    } else if(key(node) > k){
    	return searchAVL(left(node), k)
    } else{
		return searchAVL(right(node), k)
    }
}

수행시간은 트리의 높이에 영향 받아 O(logN)이다.

삽입

여기서부터는 BST 로직에서 균형검사 로직이 추가된다.

Alg insert(k)
	input key k
    output none

node <- searchAVL(root(), k)
if(!isExternal(node))
	return

key(node) <- k
expandExternal(node)
searchAndFixAfterInsert(node)	//삽입 후 균형 검사
return

insert()는 BST처럼 노드를 찾고 데이터를 넣고 외부노드를 내부노드로 확장까지 한다. 여기서 추가적으로 균형 검사를 수행한다. 균형 검사에 대한 알고리즘은 삭제까지 다룬 후 뒤에서 같이 설명할 것이다.

삭제

Alg remove(k)
	input key k
    output element with key k

rmNode <- searchAVL(root(), k)
if(isExternal(rmNode))
	return invalidException

rmElement <- key(rmNode))

rmChild <- left(rmNode)		//삭제노드 자식 여부 검사
if(!isExternal(rmChild))
	rmChild <- right(rmNode)

if(isExternal(rmChild)){
	zs <- reduceExternal(rmChild) //zs : rmChild의 형제노드
} else{
	succ <- inOrderSucc(rmNode)
    succChild <- left(succ)
    key(rmNode) <- key(succ), element(rmNode) <- element(succ)
    zs <- reduceExternal(succChild)	//zs : succChild의 형제노드
}
searchAndFixAfterRemove(parent(zs))	//zs의 부모를 검사에 전달
return rmElement

BST와 마찬가지로 rmNode를 찾고 탐색 결과가 외부노드라면 exception을 터트린다. 내부노드라면 삭제노드의 자식 여부를 검사하고 case를 자식이 꽉 차있는 경우와 그렇지 않은 경우로 나눈다. 꽉 차있는 경우에는 중위순회후계자를 찾고 그렇지 않은 경우에는 바로 노드 축소 메서드를 호출한다. 노드 축소 메서드에 전달할 노드는 각각 중위순회후계자의 왼쪽 자식과 삭제노드의 외부노드인 자식이다. 공통적으로 외부노드를 전달한다.

Alg reduceExernal(exNode)
	input external node
    output sibling of external node

exParent <- parent(exNode)
exSibling <- sibling(exNode)

if(isRoot(exParent)){
	parent(exSibling) <- NULL
    root() <- exSibling
} else{
	exGrandParent <- parent(exParent)
    if(left(exGrandParent) = exParent){
		left(exGrandParent) <- exSibling
        parent(exSibling) <- exGrandParent
    } else{
    	right(exGrandParent) <- exSibling
        parent(exSibling) <- exGrandParent
    }
}

putNode(exParent)
putNode(exNode)
return exSibling

노드 축소 메서드는 BST와 동일하다.

이제 이번 포스팅에서 가장 중요한 균형 검사 관련 메서드를 알아보자.

균형 검사 메서드

탐색, 삽입, 삭제 메서드를 알아보았는데 BST에서 AVL 트리에서 추가된 메서드는 searchAndFixAfterInsert()와 searchAndFixAfterRemove()다.

두 메서드는 updateHeight(), isBalanced(), restruct() 메서드를 공유해 우리가 다룰 메서드는 총 5가지다.

삽입 시 균형 검사

Alg searchAndFixAfterInsert(w)
	input internal node w
    output none

/*
* 전달된 노드는 삽입노드. 높이를 설정한다.
*/
w.left.height, w.right.height, w.height <- 0, 0, 1

if(isRoot(w))
	return

z <- parent(w)
while(updateHeight(z) & isBalanced(z)){
	if(isRoot(z))
    	return
    z <- parent(z)
}

if(isBalanced(z))
	return

y <- left(z)						//y 설정
if(z.right.height > y.height)
	y <- right(z)

x <- left(y)						//x 설정
if(y.right.height > x.height)
	x <- right(y)

restruct(x, y, z)		//x, y, z 개조, 불균형 수리
return

알고리즘 설명에 앞서 노드에 대한 변수이름을 w, x, y, z로 했다. 알고리즘을 설명하는 데에 조금 더 직관적인 변수명을 찾고 싶었지만 그러지 못해 아쉽다.

현재 전달된 node w는 삽입한 노드다. 삽입 과정을 상기해보면 외부노드를 찾고 데이터를 집어 넣고 외부노드를 내부노드로 확장 후 위의 메서드를 호출한다. 따라서 방금 삽입한 따끈따끈한 노드와 그의 자식들의 높이를 먼저 설정해준다.

이제 삽입한 노드 w의 부모들을 따라가면서 쭉쭉쭉 검사를 진행한다. 부모들을 따라 올라가다가 루트노드를 만나게 되면 검사는 종료된다. 루트노드에 도착하기까지 트리의 밸런스가 맞다면 x나 y를 설정하고 불균형을 수리할 필요가 없다.

삽입한 노드가 루트인지 먼저 검사를 하고 node z에 w의 부모노드를 연결한다. w의 부모노드를 연결하는 이유는 w의 밸런스를 검사할 필요가 없기 때문이다.

이제 z는 while문에 들어간다. while문의 조건을 보니 높이를 업데이트하고 밸런스가 참인 동안 반복한다. 높이 업데이트와 밸런스 판단은 잠시 뒤에 다룬다. 반복문에서도 마찬가지로 루트까지 도착을 했는데도 트리 밸런스를 만족하면 리턴해주면 된다. 반복문에서 z는 루트까지 올라간다.

반복문을 끝마쳤는데도 아직도 리턴이 안 되었다면, 이는 높이 불균형을 어딘가 찾았다는 이야기다. 여기서 z를 활용해 y를 찾고, y를 활용해 x를 찾는다. x와 y를 찾을 때는 항상 높이가 높은 노드로 설정한다.

x, y, z를 모두 지정한 후 마지막으로 restruct()에 노드 3개를 전달한다. restruct()도 잠시 뒤에 다를 것이다.

그림 예시

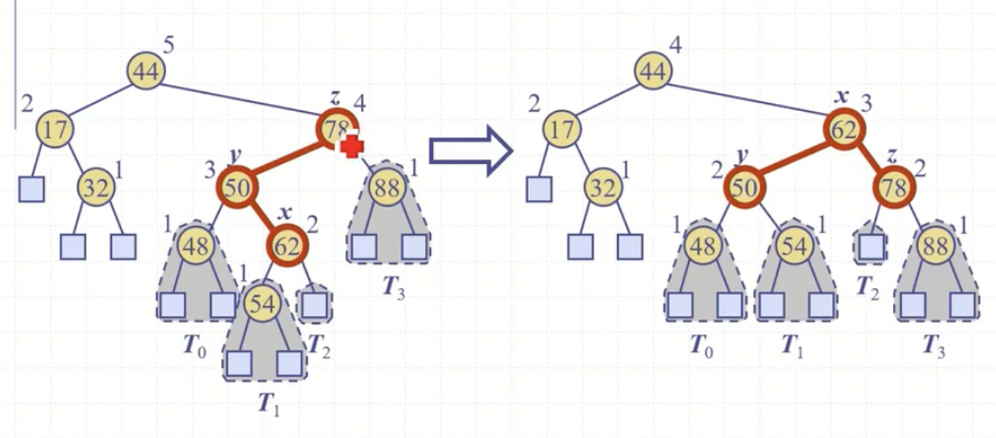
코드적으로만 떠들어 대니 이해가 조금 어려운 것 같다.

그림은 '54' 노드가 삽입되고 검사를 하고 있다. '54'는 지금 루트노드가 아니기 때문에 z가 그의 부모 '62'를 가리키게 하고 높이 업데이트와 밸런스 검사를 진행한다.

z가 '62'일 때, 좌우 높이는 1과 0이다. 그러면 부모 '50'으로 올라간다. '50'에서 바라 봤을 때 좌우 높이는 1과 2다. 그러면 또 올라간다. 어디까지 올라가는 것인가? 밸런스가 맞으면 루트까지 올라간다. 그래야 리턴받을 수 있다. '78'에서 바라보니 좌우 높이는 3과 1이다. 이제 z는 멈춘다. z는 '78'이 된다.

y -> x의 순으로 노드를 결정할 것이다. z의 자식들의 높이는 3과 1이다. 높이가 높은 '50' 노드가 y가 된다. y의 자식들 높이는 2와 1이다. 높이가 높은 '62' 노드가 x가 된다.

x(62), y(50), z(78)을 restruct에 전달하고 트리의 불균형을 수리하면 그림의 우측으로 트리 구조가 변한다.

삭제 시 균형 검사

Alg searchAndFixAfterRemove(z)
	input internal node z
    output none

while(updateHeight(z) & isBalanced(z)){
	if(isRoot(z))
    	return
    
    z <- parent(z)
}

if(isBalanced(z))
	return

y <- left(z)			//y 설정
if(z.right.height > y.height)
	y <- right(z)

x <- left(y)			//x 설정	
if(y.right.height > x.height){
	x <- right(y)
} else if(y.right.height = x.height){
	if(left(z) = y)
    	x <- left(y)
    else
    	x <- right(y)
}

b <- restruct(x, y, z)	//불균형 수리 후 리턴값을 b에 저장

if(isRoot(b))
	return
searchAndFixAfterRemove(parent(b))
return

삭제 후 검사는 내부노드를 전달 받아 수행한다. 삭제 알고리즘을 보면 reduceExternal()의 리턴 노드의 부모노드를 searchAndFixAfterRemove()에 전달한다. 따라서, 항상 내부노드만을 함수에 전달한다.

전달노드부터 높이 갱신과 트리 밸런스 체크를 진행하면서 부모노드를 타고 올라간다. 루트까지 균형이 확인되면 수리할 필요 없고 불균형이 발견되면 y와 x를 설정한다.

추후 restruct()에 x, y, z를 전달해 노드 b에 리턴받고 b의 부모노드를 재귀로 한 번 더 검사한다. restruct()의 수행으로 b를 루트로 하는 부트리의 균형은 지역적으로 복구되지만, 메서드 수행에 의해 b를 루트로 하는 부트리의 높이가 1이 줄어들었을 가능성이 있고 그로 인해 b의 부모들을 확인했을 때, 트리 전체는 균형을 잃은 상태로 있을 수 있기 때문이다. 즉, 한 번의 restruct()로는 트리의 균형을 전역적으로 회복하지 못 할 가능성이 있다.

그림 예시

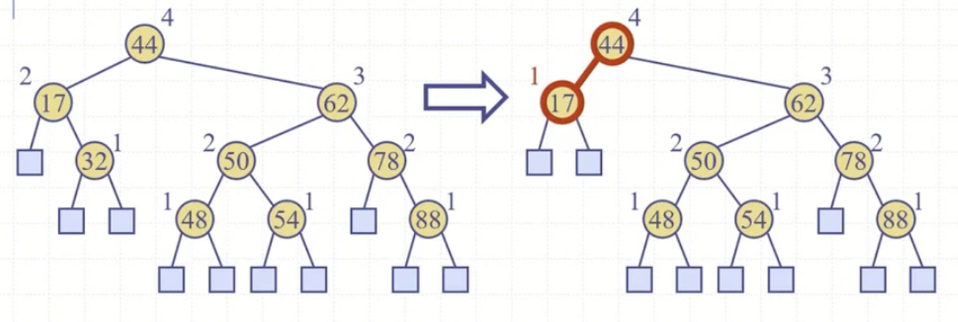
그림은 '32' 노드가 삭제되고 트리의 균형을 잃은 상태다. 노드를 삭제 후 '17' 노드가 searchAndFixAfterRemove()에 전달된다. 부모까지 올라가보니 루트노드인 '44'노드에서 불균형이 발견되었고 이 노드는 z가 된다.

'44' 노드 기준으로 높이가 높은 '62' 노드가 y가 된다. y를 기준으로 높이가 같기 때문에 y가 z의 오른쪽 자식이므로 y의 오른쪽 자식인 '78' 노드가 x가 된다.

restruct()에는 '44', '62', '78' 노드가 전달된다. restruct는 트리 불균형을 해소한 후 '62' 노드를 반환하게 되는데 해당 노드는 루트 노드이기 때문에 searchAndFixAfterRemove()를 다시 호출하진 않고 메서드는 종료된다.

높이 갱신

Alg updateHeight(node)
	input internal node 
    output boolean

h <- max(node.left.height, node.right.height) + 1

if(node.height != h){
	node.height <- h
    return true
}
return false

높이 수정은 다소 단순하다. h는 입력 노드의 자식들 높이값 중 큰 놈보다 1이 큰 놈을 저장한다. 만약 입력 노드의 높이가 h가 아니라면 즉, 갱신해줘야 할 여지가 있으면 true를 반환하고 그렇지 않으면 false를 반환한다.

균형 체크

Alg isBalanced(node)
	input internal node
    output boolean

return abs(node.left.height - node.right.height) < 2

입력 노드의 왼쪽 자식과 오른쪽 자식의 높이 차이가 절댓값 2보다 작으면 true를 반환하고 2보다 크거나 같으면 false를 반환한다. false는 균형이 지금 맞지 않다는 것을 의미한다.

삭제 검사, 삽입 검사에서 while()의 조건을 보면 updateHeight()가 균형 체크보다 먼저 수행되는 이유다. 높이를 갱신해준 후 균형을 체크해본다. 둘 다 true라면 반복문에 남아 있는다.

불균형 수리

포스팅의 마지막 관문이다. 불균형을 어떻게 수리하는지에 대해 알아보자.

Alg restruct(x, y, z)
	input node x, y, z
    output internal node

if(key(x) < key(y) < key(z)){			//x < y < z
	a <- x, b <- y, c <- z
    T0 <- a.left, T1 <- a.right, T2 <- b.right, T3 <- c.right
} else if(key(z) < key(y) < key(x)){	//z < y < x
	a <- z, b <- y, c <- x
    T0 <- a.left, T1 <- b.left, T2 <- c.left, T3 <- c.right
} else if(key(y) < key(x) < key(z)){	//y < x < z
	a <- y, b <- x, c <- z
    T0 <- a.left, T1 <- b.left, T2 <- b.right, T3 <- c.right
} else{									//z < x < y
	a <- z, b <- x, c <- y
    T0 <- a.left, T1 <- b.left, T2 <- b.right, T3 <- c.right
}

if(isRoot(z)){ 	//입력 노드 중 가장 상위 노드가 루트라면
	parent(b) <- NULL
    root <- b
} else if(left(parent(z)) = z){
	left(parent(z)) <- b
    parent(b) <- parent(z)
} else{
	right(parent(z)) <- b
    parent(b) <- parent(z)
}

left(a), right(a) <- T0, T1		//a와 T0, T1 연결
parent(T0), parent(T1) <- a
updateHeight(a)

left(c), right(c) <- T2, T3		//c와 T2, T3 연결
parent(T2), parent(t3) <- c
updateHeight(c)

left(b), right(b) <- a, c		//b와 a, c 연결
parent(a), parent(c) <- b
updateHeight(b)
	
return b

코드가 복잡해 보이니 바로 그림을 보며 이해해보자.

그림 예시

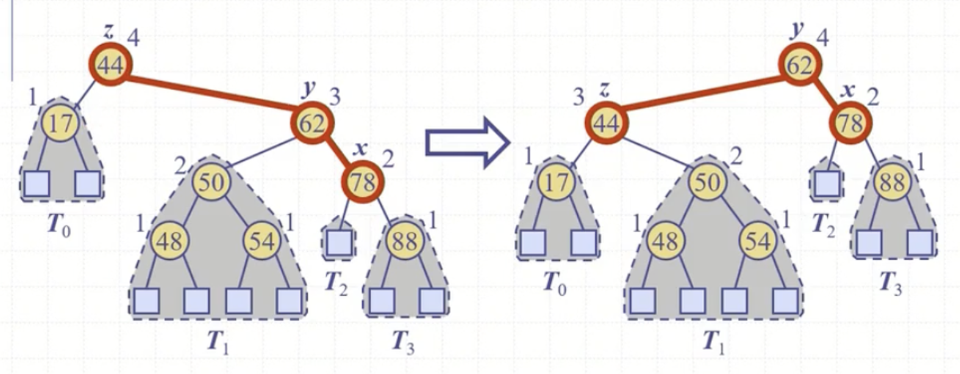
그림의 예시는 키값이 z < y < x 인 경우다. restruct()에 들어가자마자 키값에 따라 a, b, c와 T0, T1, T2, T3를 정한다.

z < y < x에서 a, b, c는 각각 z, y, x가 된다. T0는 z의 왼쪽 부트리, T1은 y의 왼쪽 부트리, T2와 T3는 각각 c의 왼쪽 부트리, 오른쪽 부트리가 된다.

설정을 마치면 z(그림에서 '44' 노드)에 대해 조건문을 수행한다. 그림에서 z는 루트노드이기 때문에 불균형 수리 후 루트노드가 될 b(그림에서 y)를 루트노드로 세팅한다.

다음 불균형 수리 후 a(그림에서 z)의 부트리가 될 T0, T1을 연결한다. 서로 연결을 마치면 a를 updateHeight()에 전달해 a의 높이를 갱신한다.

불균형 수리 후 c(그림에서 x)의 부트리가 될 T2, T3를 연결한다. 연결 후 마찬가지로 c를 updateHeight()에 전달해 c의 높이를 갱신한다.

불균형 수리 후 b(그림에서 y)의 부트리가 될 a, c를 연결한다. 마찬가지로 b를 updateHeight()에 전달해 b의 높이를 갱신한다. 마지막으로 가장 최상위 노드인 b를 리턴하며 메서드를 종료한다.

AVL 트리 성능

높이의 균형을 유지시켜 탐색과 삭제, 삽입은 모두 O(logN) 시간에 수행된다.

삽입 후 검사와 삭제 후 검사 역시 O(logN)이다. 입력 노드의 부모를 타고 루트를 향해 올라가기 때문이다.

높이 갱신, 균형 체크, 불균형 수리는 상수 시간에 수행된다. 불균형 수리는 코드가 복잡해보이지만 결국 트리를 여기 떼었다 저기 붙였다이기 때문에 O(1)이다.

공간은 O(N)만큼 사용해 외부 메모리를 사용하지 않는다.

AVL 트리는 BST의 단점을 극복하는 데 충실한 알고리즘이다. 그렇지만, 트리 구조를 자주 변경하고 높이 비교를 위한 공간을 추가적으로 마련한다는 것은 A부터 Z까지 모든 면에서 나은 알고리즘은 아니다. 트리 구조를 restruct하는 작업도 연결 트리에 국한해 O(1) 시간이다. 배열을 사용할 경우에는 이보다 더 많은 부담이 가해진다.

참고 : 국형준. 알고리즘 원리와 응용. 21세기사, 2018.