[자료구조/알고리즘] - 기초수학

미미·2024년 8월 16일
경우의 수순열재귀함수점화식조합지수와 로그집합
0

algorithm

목록 보기
6/7

집합(Set)

  • 특정 조건에 맞는 원소들의 모임
  • 집합 표현 방법

    1. 원소나열법

      A ={1,2,3,4,5}, B={2,4,6,8,10}

    2. 조건제시법

      A = {A | A는 정수, 1≤ A ≤ 5},

      B = {2B | B는 정수, 1≤ B ≤ 5}

    3. 벤 다이어그램


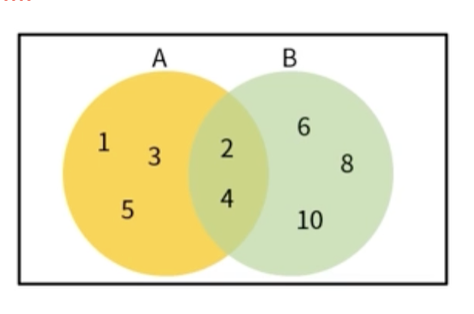
HashSet

간단한 사용법

HashSet set1 = new HashSet();
set1.add(1);
set1.add(1);
set1.add(1);
System.out.println("set1 = " + set1); //HashSet은 중복 허용 x -> 1 만 출력
set1.add(2);
set1.add(3);
System.out.println("set1 = " + set1); // set1 = [1, 2, 3]
set1.remove(1); //인덱스가 아닌 해당 값 삭제
System.out.println("set1 = " + set1); // set1 = [2, 3]
System.out.println(set1.size()); // 2
System.out.println(set1.contains(2)); // true

HashSet을 이용한 여러가지 집합 구현

HashSet a = new HashSet(Arrays.asList(1, 2, 3, 4, 5));
HashSet b = new HashSet(Arrays.asList(2, 4, 6, 8, 10));

// 교집합
// 두 집합이 공통으로 포함하는 원소로 이루어진 집합
a.retainAll(b);  // a = [2, 4]

// 합집합
// 어느 하나에라도 속하는 원소들을 모두 모은 집합
a.allAll(b); // a = [1, 2, 3, 4, 5, 6, 8, 10]

// 차집합
// A(or B)에만 속하는 원소들의 집합, A-B
a.removeAll(b); // a = [1, 3, 5]

// + 여집합
// 전체집합 중 A의 원소가 아닌 것들의 집합

ArrayList를 사용한 집합 구현

class Myset {
	//ArrayList
	ArrayList<Integer> list;
	
	//생성자1
	MySet() {
			this.list = new ArrayList<Integer>();
	}
	
	//생성자2
	MySet(int[] arr) {
			this.list = new ArrayList<Integer>();
			
			for(int item: arr){
					this.list.add(item);
			}
	}
	
	// 원소 추가 (중복 X)
	public void add(int x){
		for(int item: this.list) {
				if(item == x) {
						return;
				}
		}
		this.list.add(x);
	}	
	
	// 교집합 (교집된 Set을 새로 반환)
	public MySet retainAll(MySet b) {
		MySet result = new MySet();
		
		for(int itemA: this.list) {
			for(int itemB: b.list) {
					if (itemA == itemB) {
							result.add(itemA);
					}
			}
		}
		return result;
	}
	
	// 합집합
	public MySet addAll(MySet b) {
		MySet result = new MySet();
		
		for(int itemA: this.list) {
			result.add(itemA);
		}
		for(int itemB: b.list) {
			result.add(itemB);
		}
		return result;
	}
	
	// 차집합
	public MySet removeAll(MySet b){
		MySet result = new MySet();
		
		for(int itemA: this.list) {
				boolean containFlag = false;
				
				for(int itemB: b.list) {
						if(itemA == item) {
								containFlag = true;
								break;
							}
				}
				
				if(!containFlag) {
					result.add(itemA);
				}
		}
		
		return result;
 }

경우의 수

어떤 사건에서 일어날 수 있는 경우의 가짓수

기본 선언

int[] dice1 = {1, 2, 3, 4, 5, 6};
int[] dice2 = {1, 2, 3, 4, 5, 6};

int nA = 0;
int nB = 0;
int nAandB = 0;

합의 법칙

: 사건 A 또는 사건 B가 일어날 경우의 수

=(사건 A가 일어날 경우) + (사건 B가 일어날 경우) - (사건A와 사건B의 교집합)

ex ) 두 개의 주사위를 던졌을 때 합이 3 또는 4의 배수일 경우의 수

// 기본 풀이
for(int item1: dice1){
		for(int item2: dice2) {
				if((item1+item2)% 3 == 0) {
						nA +=1;
				}
				
				if((item1+item2)% 4 == 0) {
						nB +=1;
				}
				
				if((item1+item2)% 12 == 0) {
						nAandB +=1;
				}
		}
}
int result = nA + nB - nAandB    // 20

// HashSet 이용
HashSet<ArrayList> allCase = new HashSet<>();
for(int item1: dice1) {
	for(int item2: dice2) {
		if((item1 + item2) % 3 == 0 || (item1+item2) % 4 == ){
					ArrayList list = new ArrayList(Arrays.asList(item1,item2);
					allCase.add(list); // 자동으로 중복 제거
		}
	}
}
allCase. size(); // 20

곱의 법칙

: 사건 A와 사건 B가 동시에 일어날 경우의 수

=(사건 A가 일어날 경우) * (사건 B가 일어날 경우)

ex) 두 개의 주사위 a,b를 던졌을 때 a는 3의 배수, b는 4의 배수인 경우의 수

for(int item1: dice1){
		if(item1 % 3 == 0){
			nA++;
		}
}

for(int item1: dice2){
		if(item1 % 4 == 0){
			nB++;
		}
}

int result = nA*nB; // 2

약수구하기

public ArrayList getDivisor(int num){
	ArrayList result = new ArrayList();
	
	for(int i =1;i<=(int)num/2; i++) {  // 절반까지만 돌리는 이유는 절반이상이 되는순간 나누어 떨어지는 수가 없을것이기 때문에..
			if(num%i==0) {
				result.add(i);
			}
	}
	
	result.add(num); // 자기 자신도 약수에 포함
	return result;
}

두 수의 최대공약수와 최소공배수 구하기

‼️ 최소 공배수 = 각 값들의 곱에 최대공약수로 나눈 값

//최대 공약수
//GCD : the Greatest Common Denominator
public int getGCD(int numA, int numB) {
		int gcd = -1;
		
		ArrayList divisorA = this.getDivisor(numA); // A 약수
		ArrayList divisorB = this.getDivisor(numB); // B 약수
		
		for(int itemA : (ArrayList<Integer>divisorA) {
				for(int itemB : (ArrayList<Integer>divisorB) {
						if(itemA == itemB) {
								if(itemA > gcd) {
										gcd = itemA;
								}
						}
				}
		}
		
		return gcd;
}

// 최소 공배수
// LCM : the Lowest Common Multiple
public int getLCM(int numA, int numB) {
		int lcm = -1;
		
		int gcd = this.getGCD(numA, numB);  // 최대 공약수
		
		if(gcd != -1) { // 예외적인 상황을 위해(최대 공약수가 없는 경우)
			lcm = numA * numB / gcd;
		}
		
		return lcm;
}

순열

팩토리얼(Factorial)

: 1에서 n까지 모든 자연수의 곱 (n!)

// 5!
int n=5;
int result =1;

for(int i=1;i<= n;i++) {
		result *= i;
}

순열

: 순서를 정해서 서로 다른 n개의 중에 r개를 선택하는 경우의 수 (중복 x)

  • n! / (n-r)!
// 5명을 3줄로 세우는 경우의 수
n = 5;
int r = 3;
result =1;

for(int i=n; i >= n-r+1; i--) {
		result *= i;
}

중복 순열

: 순서를 정해서 서로 다른 n개의 중에 r개를 선택하는 경우의 수 (중복 허용)

// 서로 다른 4개의 수 중에서 2개를 뽑는 경우의 수
n=4;
r=2;
result =1;

// 1. for문 사용
for(int i=0; i<r;i++) {
		result *= n;
}

// 2. Math 클래스 사용
Math.pow(n,r);

원 순열

: 원 모양의 테이블에 n개의 원소를 나열하는 경우의 수

  • n! / n
// 원 모양의 테이블에 3명을 앉히는 경우의 수
n = 3
result = 1;

for(int i=1; i<n; i++) {
		result *= i;
}

EX)

1, 2, 3, 4를 이용하여 세자리 자연수를 만드는 방법 (순서 0, 중복 X)의 각 결과를 출력

첫번째 방법

// 배열의 순서를 바꿔가며 앞의 3개의 숫자를 뽑아 세자리 자연수를 만드는 방법

// n은 배열의 개수
// r은 만드려는 자리수
// depth은 현재 자리수
void permutation(int[] arr, int depth, int n, int r){

		//재귀함수 탈출 조건 -> 출력
		if(depth == r){
				for(int i =0;i<r;i++){
						System.out.print(arr[i]) + " " );
				}
				System.out.println();
				return;
		}
		
		for( int i= depth; i<n; i++) {
				swap(arr, depth, i);  // 자리를 바꿔줌
				permutation(arr, depth+1, n, r); // 재귀함수
				swap(arr, depth, i); // 다시 원래 자리로
		}

}

// 자리를 바꿔주는 함수
void swap(int[] arr, int depth, int idx){
		int tmp = arr[depth];
		arr[depth] = arr[idx];
		arr[idx] = tmp;
}

두번째 방법

void permutation(int[] arr, int depth, int n, int r, boolean[] visited, int[] out) {

		//재귀함수 탈출 조건 -> 출력
		if(depth == r){
				System.out.println(Arrays.toString(out));
				return;
		}

		for(int i= 0; i<n; i++) {
				if(visited[i] != true) {
					visited[i] = true;
					out[depth] = arr[i];
					permutation(arr, depth +1, n, r, visited, out);
					visited[i] = false;
		}

}
  • permutation을 사용하여 특정한 조건이 맞는지 확인하고싶다면? → ArrayList를 매개변수로 추가하여 결과를 계속 저장한다.
    void permutation(int[] arr, int depth, int n, int r, boolean[] visited, int[] out, ArrayList<String> list) {

		//재귀함수 탈출 조건
		if(depth == r){
				//System.out.println(Arrays.toString(out));
				list.add(new String(out));
				return;
		}

		for(int i= 0; i<n; i++) {
				if(visited[i] != true) {
					visited[i] = true;
					out[depth] = arr[i];
					permutation(arr, depth +1, n, r, visited, out);
					visited[i] = false;
		}

}
    → 저장된 list를 이용하여 검증
    // 타입이나 길이는 예시, 변경가능
boolean[] visited = new boolean[s.length()];
char[] out = new char[s.length()]; 
ArrayList<String> list = new ArrayList<>();

permutation(array,0,length, length, visited, out, list);

for(String s:list){
	// 검증
}

조합

서로 다른 n개 중에서 r개를 선택하는 경우의 수 (순서 X, 중복 X)

= n! / (n-r)!*r!

// 조합
// 서로 다른 4명 중 주번 2명 뽑는 경우의 수
int n=4;
int r=2;

int pResul=1;
for(int i=n; i>=n-r+1; i--) {
	pResult *= i;
}

int rResul=1;
for(int i=1; i>=r; i++) {
	rResult *= i;
}

int result = pResult/rResult;

중복 조합

서로 다른 n개 중에서 r개를 선택하는 경우의 수 (순서 X, 중복 0)

static int getCombination(int n, int r) {
		int pResul=1;
		for(int i=n; i>=n-r+1; i--) {
			pResult *= i;
		}

		int rResul=1;
		for(int i=1; i>=r; i++) {
			rResult *= i;
		}
		
		return pResult/rResult;
}

// 중복조합 = getCombination(n+r-1, r));

EX)

1, 2, 3, 4를 이용하여 세자리 자연수를 만드는 방법 (순서 X, 중복 X)의 각 결과를 출력

void combination(int[] arr, boolean[] visited, int depth, int n, int r){

		if(r == 0){
				for(int i=0; i<n; i++) {
						if(visited[i]) {
								System.out.println(arr[i] + " ");
						}
				}
				System.out.println();
				return;
		}
		
		if(depth == n) {
				return;
		}
	
	
		visited[depth] = true;
		combination(arr, visited, depth +1, n, r-1);
		
		visited[depth] = false;
		combination(arr, visitied, depth +1, n, r);
}

// combination(arr, visited, 0, 4, 3);

점화식과 재귀함수

점화식

: 어떤 수열의 일반항을 그 이전의 항들을 이용하여 정의한 식

ex) 피보나치 수열 → 1, 1, 2, 3, 5, 8, 13, …. F1 = F2 =1, F(N+2) = F(N+1) + F(N)

// 첫번째 문제
// 1, 3, 9, 27, ... 의 n번째 수
int n = 4;
int result = 1;
for(int i=0; i<n; i++){
	if(i==0){
			result =1;
	}else{
			result *= 3;
	}
}

// 두번째 문제
//1, 2, 3, 4, 5, 6 의 n번째 까지의 합
int n = 5;
result = 0;
for(int i=0; i<n; i++){
	result += i;
}

// 세번째 문제
// 피보나치 수열의 n번째 수
n = 6;
result = 0;
int a1 = 1;
int a2 = 1;

if(n < 3) {
	result =1;
} else {
	for(int i=2; i<n; i++){
			result = a1+a2;
			a1 = a2;
			a2 = result;
	}
}

재귀함수

: 어떤 함수가 자신을 다시 호출하여 작업을 수행하는 방식

// 첫번째 문제 재귀함수로 구현
static int recursion1(int n) {
		if( n == 1){
				return 1;
		}
		return 3 * recursion1(n-1);
}

// 두번째 문제 재귀함수로 구현
static int recursion2(int n) {
		if( n == 1){
				return 1;
		}
		return n + recursion2(n-1);
}

// 세번째 문제 재귀함수로 구현
static int recursion3(int n) {
		if(n < 3){
				return 1;
		}
		return recursion3(n-2) + recursion3(n-1);
}

EX)

  • 팩토리얼을 재귀함수로 구현
static int factorial(int n) {
		if(n == 1){
				return 1;
		}
		return n * factorial(n-1);
}
  • 최대 공약수를 재귀함수로 구현
static int gcd(int a, int b) {
		if(a%b==0){
				return b;
		}
		return gcd(b, a%b);
}

지수와 로그

  • 제곱 : Math.pow()
  • 제곱근 : Math.sqrt()
  • 절대값 : Math.abs()
  • 로그 : Math.log() or Math.log10()
// 1. 제곱, 제곱근, 지수
System.out.println(Math.pow(2,3));  // 8
System.out.println(Math.pow(2, -3)); // 1/8 = 0.125
System.out.println(Math.pow(-2, -3)); // -1/8 = -0.125

System.out.print(Math.pow(2,30)); // 1.073741824E9
System.out.print("%.0f\n", Math.pow(2,30)); // 1073741824

// 2. 제곱근
System.out.print(Math.sqrt(16));  //4
System.out.print(Math.pow(16, 1.0/2));  //4
System.out.print(Math.pow(16, 1.0/4));  //2

// + 절대 값
System.out.print(Math.abs(5)); //5
System.out.print(Math.abs(-5)); //5  

// 3. 로그
System.out.print(Math.E); // 2.718281828459045
System.out.print(Math.log(2.718281828459045)); //1.0
System.out.print(Math.log10(1000)); //3.0
System.out.print(Math.log(4)/Math.log(2)); //2.0
profile
미미
이전 포스트

재귀함수 사용시 시간을 단축시키는 방법

다음 포스트

알고리즘 복잡도

0개의 댓글

관련 채용 정보