algorithm

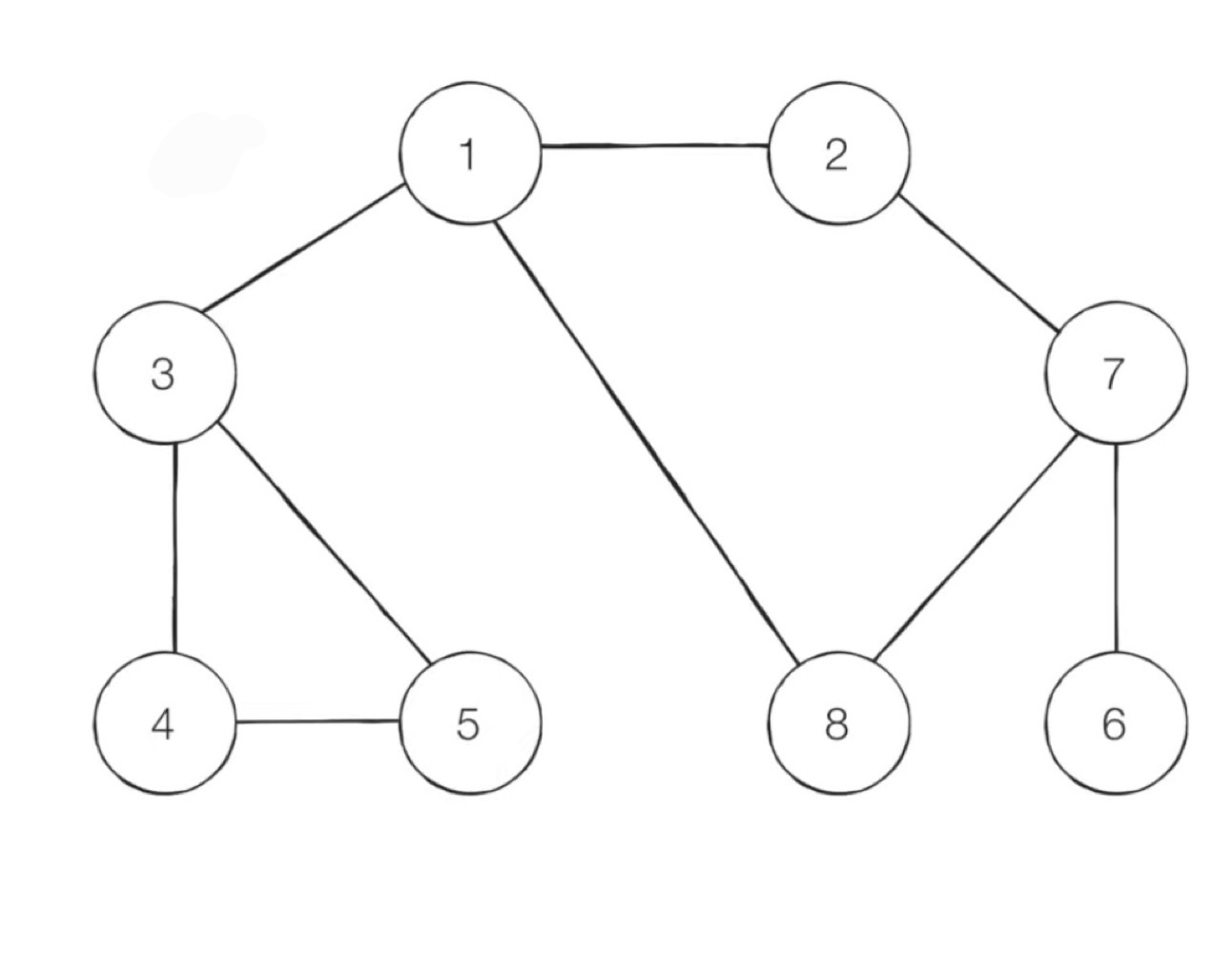
깊이 우선 탐색이라고 부르며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘\-> 스택 자료구조(혹은 재귀 함수) 이용(과정을 보여주기 위한 예시에서 노드는 1번부터 탐색은 숫자가 낮은 노드부터 하는 것으로 가정한다.)1\. 탐색 시작 노드를 스택에 삽입하고 방문

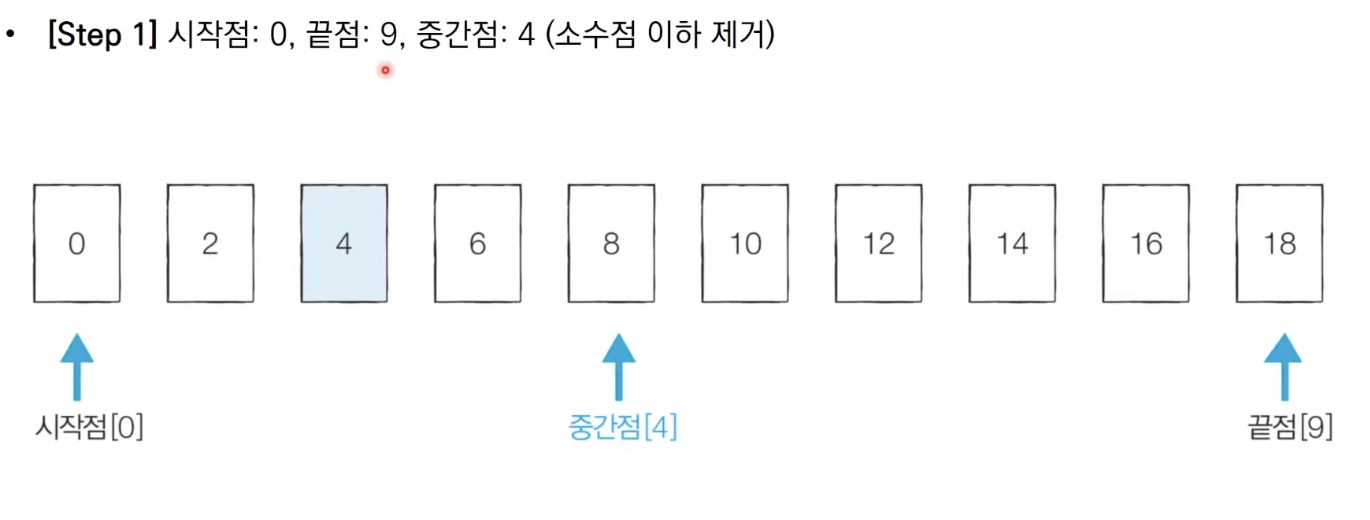
: 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법 (시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정)💡 파라메트릭 서치 문제(최적화 문제를 결정 문제(’예’ 혹은 ‘아니오’)로 바꾸어 해결하는 기법)는 이진 탐색을 이용하여 해

메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장(배열이나 리스트 사용)하여 다시 계산하지 않도록 함다이나믹 프로그래밍의 구현은 일반적으로 두가지 방식(탑다운과 보텀업)으로 구성 \-

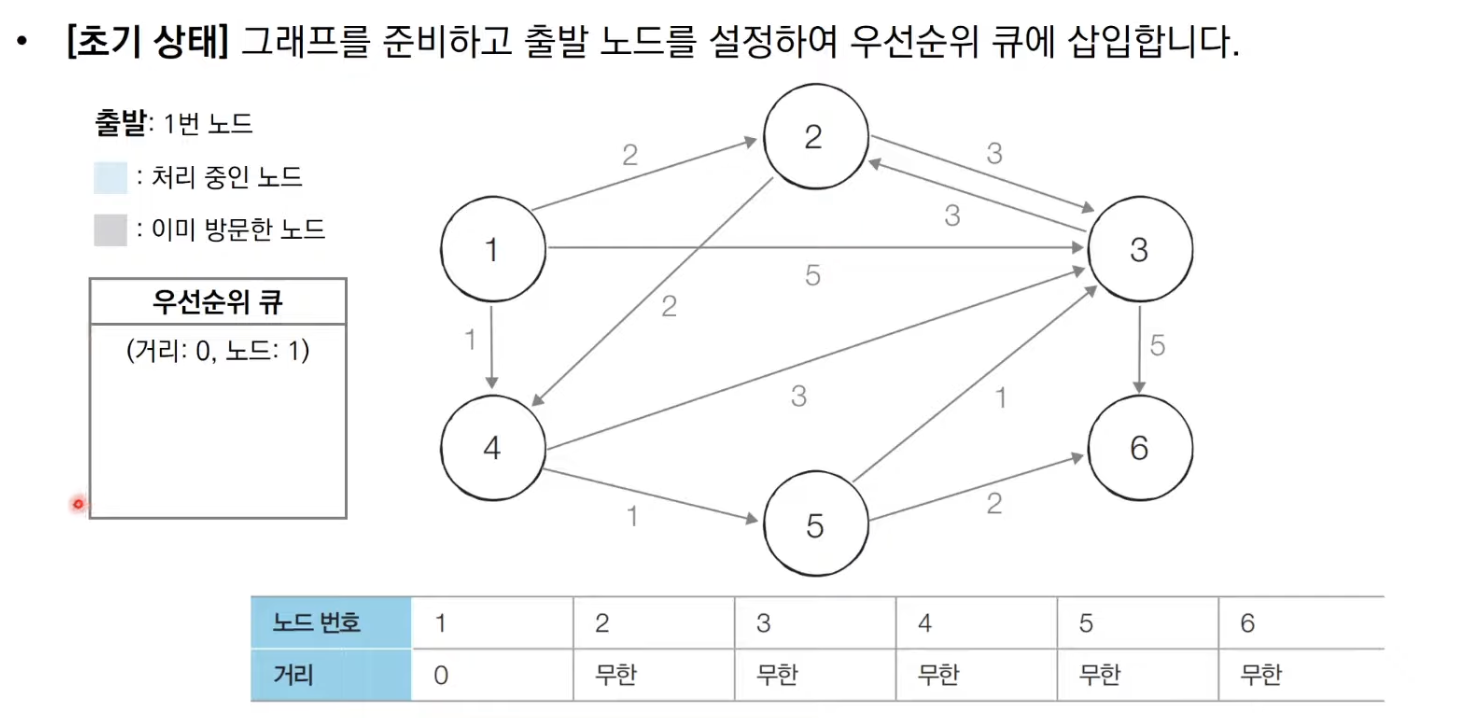
💡 최단 경로 알고리즘 : 가장 짧은 경로를 찾는 알고리즘각 지점은 그래프의 노드로 표현지점 간 연결된 도로는 그래프에서 간선으로 표현한 지점에서 다른 한 지점까지의 최단 경로한 지점에서 다른 모든 지점까지의 최단 경로모든 지점에서 다른 모든 지점까지의 최단 경로:

💡 재귀함수 재귀함수란 자기 자신을 호출하는 함수를 말합니다. ex) 피보나치 수열 하지만 재귀함수를 사용하다보면 시간복잡도가 너무 높아질때가 있습니다. 위의 예시에 나온 피보나치 수열의 시간복잡도는

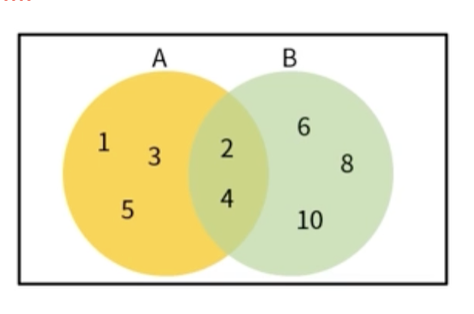
특정 조건에 맞는 원소들의 모임집합 표현 방법원소나열법A ={1,2,3,4,5}, B={2,4,6,8,10}조건제시법A = {A | A는 정수, 1≤ A ≤ 5},B = {2B | B는 정수, 1≤ B ≤ 5}벤 다이어그램간단한 사용법HashSet을 이용한 여러가지 집

: 알고리즘 성능을 나타내는 척도시간 복잡도 : 알고리즘의 필요 연산 횟수공간 복잡도 : 알고리즘의 필요 메모리→ 시간 복잡도와 공간 복잡도는 Trade-off 관계 ( 반비례 관계 ): 빅오 표기법을 통해 나타냄 → 최악의 경우빅오 표기법을 통해 나타냄일반적으로 메모