🔍정렬 알고리즘이란
정렬 알고리즘은 원소들을 일정한 순서대로 열거하는 알고리즘이다.
결과는 반드시 다음 두 조건을 만족해야 한다.
1. 출력은 비 내림차순이다.
2. 출력은 입력을 재배열하여 만든 순열이다.
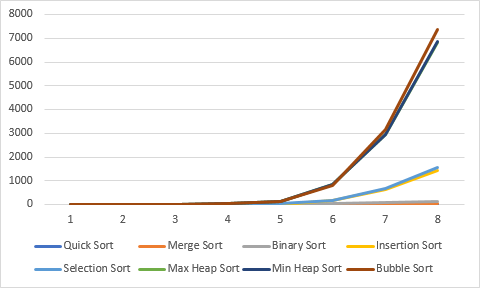
📝대표적인 정렬 알고리즘
이 글에서 다룰 정렬 알고리즘은 아래와 같다.
- 삽입 정렬(Insertion sort)
- 선택 정렬(Selection sort)
- 버블 정렬(Bubble sort)
- 병합 정렬(Merge sort)
- 퀵 정렬(Quick sort)
- 힙 정렬(Heap sort)
삽입 정렬
🔍삽입정렬이란
- 가장 기본적인 정렬 알고리즘
- 작은 배열을 정렬하거나 이미 정렬된 배열에 자료를 삽입/삭제할 때 효율적
- 시간복잡도: O(N^2)
⚙️동작원리
사전 정의
arr: 배열
i: 현재 index, 오름차순으로 탐색, 1 <= i < arr.size()
j: 이전 index, 내림차순으로 탐색, 0 <= j < i-1
알고리즘
- arr[i]보다 작은 원소가 나올 때까지 arr[j+1] = arr[j]를 반복
- arr[i] 이하인 arr[j]이거나 j < 0일 때 arr[j+1]에 arr[i]를 저장
- 마지막 index까지 1~2번 과정을 반복
💻구현
void inselectionSort(){
for(int i=1; i<N; i++){
arr[i] = temp;
for(int j = i-1; j >= 0 && arr[j] > temp; j--){
arr[j+1] = arr[j];
}
arr[j+1] = temp;
}
}선택 정렬
🔍선택 정렬이란
- k번째 순서에 넣을 원소를 선택하는 정렬 알고리즘
- 시간복잡도: θ(N^2)
⚙️동작원리
사전 정의
arr: 배열
i: 현재 index, 오름차순으로 탐색, 1 <= i < arr.size()
j: 탐색 index, 오름차순으로 탐색, i <= j < arr.size()
minIdx: 탐색 범위 중 최솟값의 index
알고리즘
- i <= j인 arr[j] 중 최솟값인 arr[minIdx]를 선택
- arr[i]과 arr[minIdx]의 값을 서로 교환
- 마지막 index까지 1~2번 과정을 반복
💻구현
void selectionSort(){
int minNum = INT_MAX, minIdx;
for(int i=0; i<N; i++){
for(int j=i; j<N; j++){
if(minNum > arr[j]){
minIdx = j;
minNum = arr[j];
}
}
arr[minIdx] = arr[i];
arr[i] = minNum;
}
}버블 정렬
🔍버블 정렬이란
- 인접한 두 원소를 비교해 서로 값을 교환하며 정렬
- 정렬을 1회 수행할 때마다 맨 마지막 index에 정렬이 완료된 데이터가 배치
- 정렬을 수행할 때마다 마지막 index가 1씩 감소
- 시간복잡도: O(N^2)
⚙️동작원리
사전 정의
arr: 배열
i: 현재 index, 오름차순으로 탐색,0 <= i < arr.size()
j: 탐색 index, 오름차순으로 탐색, 0 <= j < arr.size()
알고리즘
- arr[j]와 arr[j+1]의 값을 비교 후 정렬 방향에 맞춰 교환
- 1번 과정을 j + 1 < arr.size() -i을 만족할 동안 반복
- 1~2번 과정을 i < arr.size()을 만족할 동안 반복
💻구현
void bubleSort(){
for(int i=0; i<N; i++){
for(int j=0; j< N-1-i; j++){
if(arr[j] > arr[j+1]){
swap(arr[j], arr[j+1]);
}
}
}
}
병합 정렬
🔍병합 정렬이란
- 하나의 배열을 두개로 분할한 뒤 각자 정렬한 이후 병합
- 최악의 경우에도 O(NlogN)을 보장
- 대표적인 분할정복 알고리즘
- 시간복잡도: O(NlogN)
⚙️동작원리
알고리즘
- 배열의 길이가 0 또는 1이면 이미 정렬된 것으로 가정
- 정렬되지 않은 배열을 비슷한 크기의 두 부분 배열로 분할
- 인접한 두 부분 배열을 정렬한 후 병합
- 배열이 완성될 때까지 3번 과정을 반복
💻구현
void mergeArr(int startIdx, int mid, int endIdx){
int frontIdx = startIdx; // 앞쪽 부분배열 index
int backIdx = mid+1; // 뒷쪽 부분배열 index
int mergeIdx = startIdx; // 병합 배열 index
while(frontIdx <= mid && backIdx <= endIdx){
if(arr[frontIdx] <= arr[backIdx]){
msort[mergeIdx] = arr[frontIdx];
frontIdx++;
}
else{
msort[mergeIdx] = arr[backIdx];
backIdx++;
}
mergeIdx++;
}
if(frontIdx > mid){
for(int idx = backIdx; idx <= endIdx; idx++)
msort[mergeIdx++] = arr[idx];
}
else{
for(int idx = frontIdx; idx <= mid; idx++){
msort[mergeIdx++] = arr[idx];
}
}
for(int idx = startIdx; idx <= endIdx; idx++){
arr[idx] = msort[idx];
}
}
void mergeSort(int startIdx,int endIdx){
int sizeArr = endIdx - startIdx;
if(sizeArr < 1)return;
int mid = (startIdx+endIdx)/2;
mergeSort(startIdx, mid);
mergeSort(mid+1, endIdx);
mergeArr(startIdx, mid, endIdx);
}동작 예시
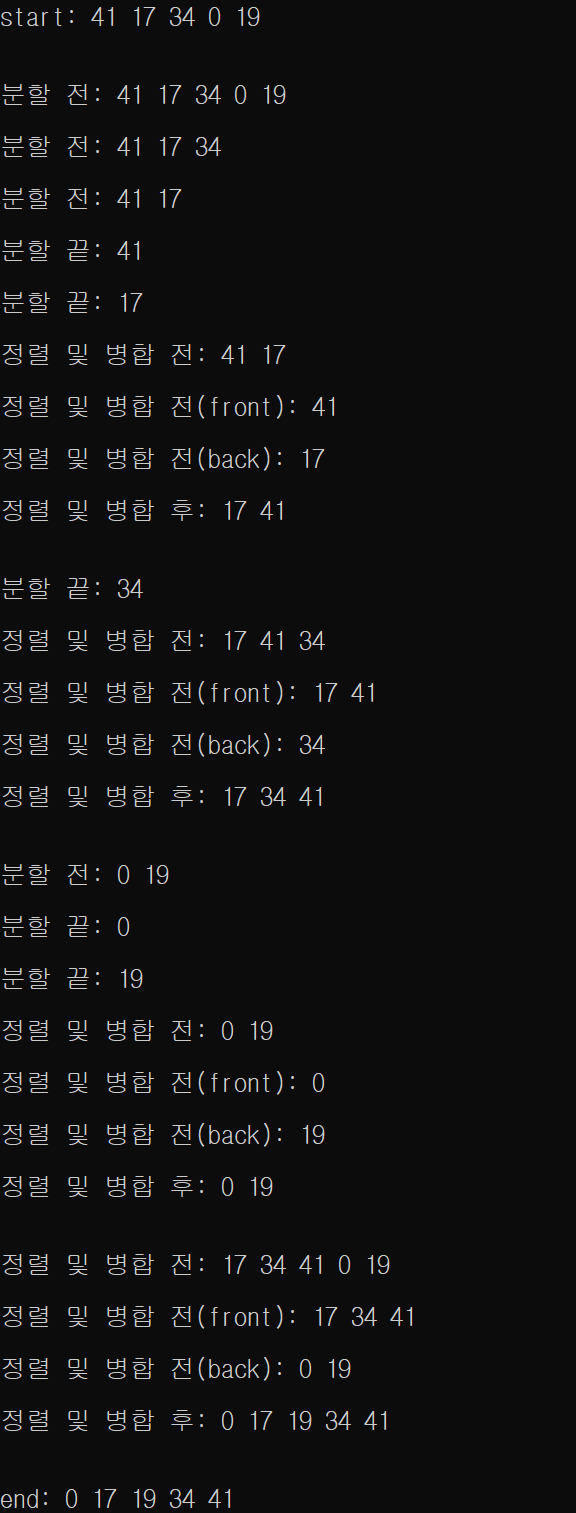
퀵 정렬
🔍퀵 정렬이란
- 분할 정복 알고리즘의 하나로 평균적으로 매우 빠른 수행속도의 정렬
- 병합 정렬과 달리 배열을 pivot을 기준으로 비균등하게 분할
- 시간복잡도: O(NlogN)
⚙️동작원리
사전 정의
arr: 배열
startIdx: 시작 index
endIdx: 끝 index
pivot: 퀵 정렬의 기준이 되는 원소, 이 글에선 첫번째 원소로 지정
low: pivot보다 큰 원소를 탐색하는 index, 오름차순으로 탐색
high: pivot보다 작은 원소를 탐색하는 index, 내림차순으로 탐색
알고리즘
- 첫번째 원소를 pivot으로 지정
- low와 high로 배열 탐색
- low는 arr[low] > pivot인 원소가 나오면 정지
- high는 arr[high] < pivot인 원소가 나오면 정지
- low와 high가 가리키는 두 원소를 서로 교환
- 2~3번 과정을 low와 high가 엇갈릴 때까지 반복
- pivot과 arr[high]의 값을 서로 교환
- pivot을 기준으로 왼쪽 배열(<=pivot)과 오른쪽 배열(>=pivot)로 분할
- 배열의 크기가 1 이하가 될 때까지 분할된 배열에서 각각 1~5번 과정을 반복
💻구현
void quickSort(int startIdx, int endIdx){
int sizeArr = endIdx - startIdx;
if(sizeArr <= 1) return;
int pivotIdx = startIdx, low = startIdx+1, high = endIdx;
while(true){
while(low < endIdx && arr[low ] <= arr[pivotIdx]) low ++;
while(high > startIdx && arr[high] >= arr[pivotIdx]) high--;
if(low >= high){
swap(arr[high], arr[pivotIdx]);
pivotIdx = high;
break;
}
else
swap(arr[low], arr[high]);
}
printArr(arr, startIdx, endIdx+1);
quickSort(startIdx, pivotIdx-1);
quickSort(pivotIdx +1, endIdx);
}동작 예시
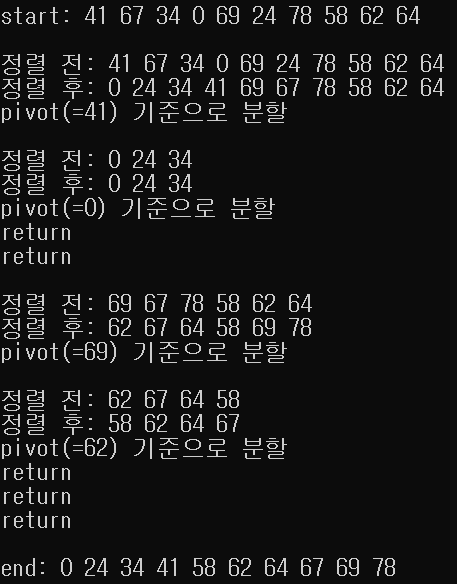
힙 정렬
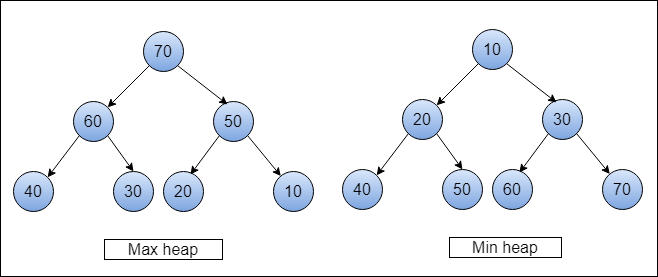
🔍힙(heap) 이란
- 완전 이진 트리의 일종으로 최댓값, 최솟값을 쉽게 추출할 수 있는 자료구조
🔍힙 정렬이란
- 최대 힙 트리/최소 힙 트리를 구성해 정렬
- 부모 노드가 자식노드를 비교해 정렬 방향에 맞게 교환
- 최대 힙의 경우 부모노드가 자식노드보다 큼
- 최소 힙의 경우 부모노드가 자식노드보다 작음
- 시간복잡도: O(NlogN)
⚙️동작원리
사전 정의
index에 규칙성을 부여해 배열로 이진 트리를 구성한다.
child: 자식노드인 index
parent: 부모노드인 index, (child - 1) // 2
left: 왼쪽 자식노드인 index, left = parent x 2 + 1
right: 오른쪽 자식노드인 index, right = parent x 2 + 2
알고리즘
- 완전 이진 트리를 구성 (루트 노드 > 부모노드 > 왼쪽 자식노드 > 오른쪽 자식노드 순)
- 최대/최소 힙을 구성
- root 노드와 최하단의 자식노드의 정보(index)를 교환
- 최하단 자식노드를 정렬에서 제외
- root노드만 남을 때까지 2~4번 과정을 반복
💻구현
void heapify(int parent, int treeSize){
int left = parent *2 +1;
int right = parent *2 +2;
int maxIdx = parent;
if(left < treeSize && arr[left ] > arr[maxIdx]) maxIdx = left;
if(right < treeSize && arr[right] > arr[maxIdx]) maxIdx = right;
// 최댓값을 가지는 노드 탐색
if(maxIdx != parent){
swap(arr[parent], arr[maxIdx]);
heapify(maxIdx, treeSize);
} // 부모노드의 값이 최대가 아닌 경우 최댓값과 부모노드의 값을 swap,
//최댓값을 가졌던 자식노드를 매개변수로 삼아 재귀
}
void heapSort(){
for(int i = (N-1)/2; i>=0; i--){
heapify(i, N);
//최하단 자식노드의 부모노드부터 root노드까지 반복해 전체 tree를 최대 heap 구조로 배치
}
for(int treeSize = N -1; treeSize >= 0; treeSize--){
swap(arr[0], arr[treeSize]);
heapify(0, treeSize);
}
}