[백준] 1463번: 1로 만들기

💡 문제 설명

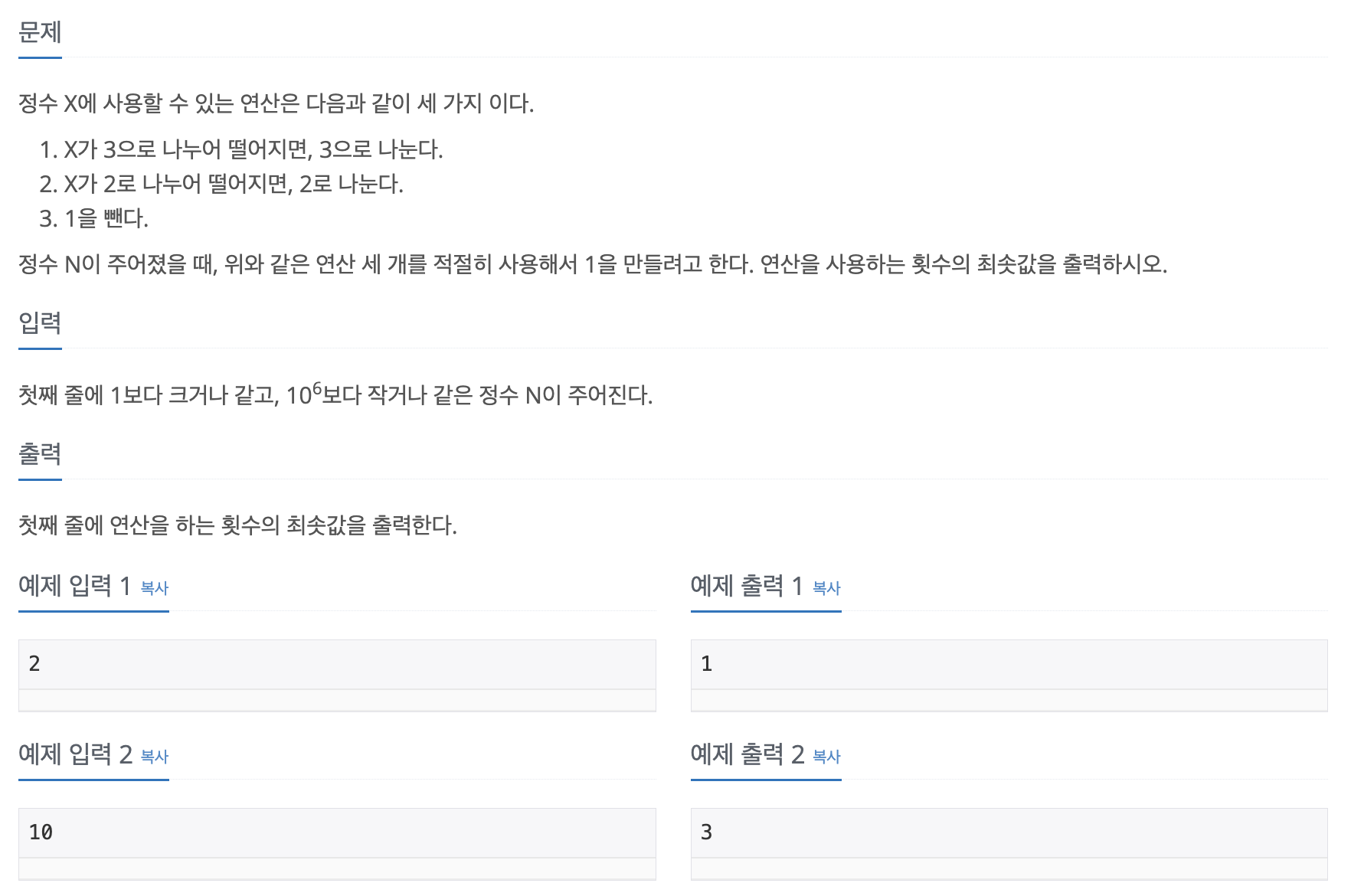
어떤 수 N이 주어졌을 때, 3가지의 연산을 활용해 1로 만드는 최소 횟수를 구하면 된다. 처음 봤을 때 백준 2579번: 계단 오르기와 유사하다는 느낌을 받아 Dynamic programming(동적 계획법)을 활용코자 했다.

추가적으로 이 DP는 상향식(Bottom-Up)과 하향식(Top-Down) 두 가지 접근법이 존재한다. 상향식은 제일 작은 인덱스에서 목표 인덱스로 이르는 순서로 계산되고 일반적으로 for문으로 구현한다(정답은 따라서 맨 마지막 인덱스에 해당하는 값이 된다). 하향식은 큰 문제를 해결하기 위해 작은 문제를 재귀적으로 푸는 방식이다. 재귀로 구현한다.

💡풀이

✍️ 내 풀이: DP(상향식)

N = int(input())
dp = [0] * (N + 1)

if N == 1:
    print(0)

else:
    for i in range(2, N+1):
        
        if i % 6 == 0: # 2와 3으로 나누어 떨어지는 경우
            t = min(dp[i-1], dp[i//3], dp[i//2])
            dp[i] = t+1

        elif i % 3 == 0:
            t = min(dp[i-1], dp[i//3])
            dp[i] = t+1

        elif i % 2 == 0:
            t = min(dp[i-1], dp[i//2])
            dp[i] = t+1
        
        else:
            dp[i] = dp[i-1] + 1

    print(dp[-1])

변수 dp에 해당 숫자를 1로 만드는 최소 연산 횟수를 for 문을 통해 저장하여 풀었다. 이전 인덱스 또는 2와 3으로 나눈 인덱스에 해당하는 값 중 가장 작은 값에 +1 한 값을 해당 i번째 인덱스에 저장했다.

✍️ GPT의 풀이(클린 코드)

위의 내 풀이는 if/elif/else 구문으로 풀었는데, 사실 더 간단한 코드로 각각의 문제 해결이 가능하다. GPT가 작성한 코드를 보고 힌트를 얻었다.

dp[i] = dp[i - 1] + 1

if i % 2 == 0:
	dp[i] = min(dp[i], dp[i // 2] + 1)

if i % 3 == 0:
	dp[i] = min(dp[i], dp[i // 3] + 1)

이렇게 if/if로 두면 2와 3으로 동시에 나눠지는 경우의 문제를 보다 적은 코드로 해결할 수 있다.

✍️ 기타 풀이법

해당 문제는 당연히 하향식 DP로도 가능하다. 또한, 다른 분의 풀이를 보고 BFS로도 풀이가 가능하다는 것을 알 수 있었다. BFS는 가중치가 없거나 모두 동일한 그래프에 대해서 항상 최단거리를 보장한다. 이유는 가장 한 단계씩 탐색하며 깊이가 낮은 노드(정점)부터 순서대로 탐색하기 때문. 그래프 접근으로도 풀 수 있다는 점이 신선했다.