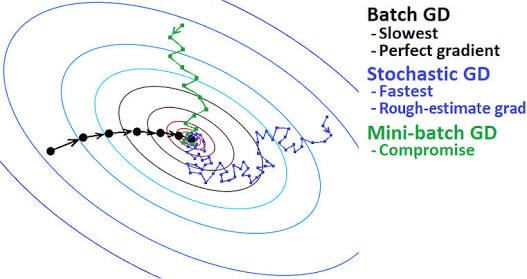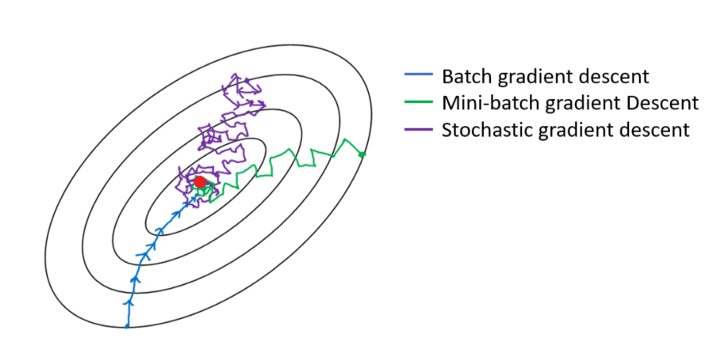
경사 하강법으로 손실 값을 최적화(optimization)하기 위한 최적화 알고리즘(optimizer)은 다양하며 대표적으로 세 가지 정도의 변형이 있으며, 목적 함수의 기울기 계산에 사용하는 데이터의 양이 다름
데이터의 양에 따라 최적인 최솟값을 찾는 정확성과 최솟값을 찾는 데 걸리는 시간 간의 균형을 맞추기 위해 다른 방법들을 적용할 수 있음
배치 경사 하강법 (Batch Gradient Descent, Vanilla Gradient Descent)
경사 하강법을 위한 기울기를 계산할 때, 모든 학습 데이터셋을 사용하여 손실(loss)을 계산한 뒤 손실이 최소가 되도록 모델의 가중치(기울기)를 업데이트 하는 방법
해당 방법에서 배치(batch)란 일부 데이터가 아닌 학습에 사용되는 전체 데이터를 의미함을 주의
※ 여기서 손실(loss)은 머신러닝 모델이 입력 데이터에 의해 예측하는 값과 실제 출력 값 간의 차이라고만 일단 이해해보자 (추후 다룰 예정)
장점
- 가중치 업데이트를 위한 계산 횟수가 효율적임
모든 학습 데이터를 사용하여 손실을 한 번씩 계산하므로 - 전체 학습 데이터에 대해 계산하므로 손실 함수가 전역 혹은 지역 최소값으로 수렴하는 것이 보장됨
단점
- 데이터 세트의 규모가 클 경우 학습을 위한 수행 시간이 다른 방법에 비해 오래 소요됨
학습되는 모든 데이터를 하나 씩 대입하면서 각 데이터 별 손실 값을 저장하기 위해 메모리가 사용되는데 전체 데이터에 대한 손실들을 저장하기 위해서 메모리가 사용되므로 메모리 소비가 높아 계산이 느림
모델 업데이트에 크게 기여하지 않는 예제 또한 모두 살펴보게 됨 - 온라인 형태의 학습이 어려움
※ 여기서 온라인 학습이란, 학습에 사용할 수 있는 데이터가 순차적으로 계속해서 늘어나는 과정에서 연속적으로 데이터를 받고 학습시킬 수 있는 방식을 의미
배치 경사 하강법은 모든 학습 데이터 셋을 사용해야 하므로 초기에 모델 학습에 사용된 계속 보유하고 있어야하며 연속적으로 들어오는 데이터만을 사용한 모델 학습이 불가능함
이론적으로는 기존 보유한 학습 데이터 + 새로 들어온 데이터 세트를 사용해서 모델을 다시 학습해야 함 (오프라인 학습)
미니 배치 경사 하강법 (Mini-batch Gradient Descent, MGD)
미니 배치 크기 만큼의 데이터를 기반으로 경사 하강법을 적용하는 방법
※ 파이썬으로 딥러닝, 머신러닝 등 학습 메소드에서 batch_size 등과 같은 매개변수를 접할 수 있는데, 만약 전체 학습 데이터가 20000개이고, batch size를 20으로 하면 1000개의 미니 배치가 생성되는 것
배치 경사 하강법에서는 모든 학습 데이터를 사용하여 손실을 계산한 뒤 모델이 업데이트 된다고 하였으나, 여기에선 미니 배치 수만큼의 데이터를 사용하여 손실을 계산하고 모델이 업데이트됨
- 기존 데이터의 순서를 피하기 위해 훈련 데이터 세트를 무작위로 선택
- 훈련 데이터 세트를 배치 크기에 따라 n개의 미니 배치로 분할
장점
- Batch Gradient Descent와 Stochastic Gradient Descent의 중간점
- Batch Gradient Descent보다 적은 데이터를 사용하기에 수행 속도가 더 빠름
- 무작위로 미니 배치를 설정하기에 중복 데이터나 학습에 크게 기여하지 않는 데이터를 피하는 데 도움이 됨
- 학습되는 배치가 훈련 세트의 크기보다 작기 때문에 학습 프로세스에 노이즈를 추가해서 일반화 성능을 개선하는데 도움이 됨
단점
- 배치 경사 하강법에 비해 최적의 최소값으로 수렴하는 것에 대한 보장이 어려움
- 미니 배치 수가 적을수록 모델 업데이트로 인항 기울기 추정의 정확도가 떨어짐
확률적 경사 하강법 (Stochastic Gradient Descent, SGD)
모델의 가중치 업데이트 시 한 개의 데이터만을 사용하여 계산하는 경사 하강법
배치 경사 하강법은 모든 학습 데이터를 사용하여 손실 계산 후 가중치 업데이트
확률적 경사 하강법은 각각 한 데이터 마다 손실 계산 후 가중치 업데이트
장점
- 모든 데이터에 대해 가중치를 업데이트 하므로 가중치 업데이트 속도가 더 빠름 (위 방법들과 비교했을 때 가장 빠름)
- 모델이 한 번 업데이트 될 때 하나의 데이터 포인트만을 사용하므로 메모리 소비가 낮음
단점
- 가중치를 업데이트 하는 속도 자체는 한 번 모델을 업데이트할 때 예시(데이터)가 하나만 사용되므로 더 많이 반복해서 실행해야 할 수 있으며 분산이 커짐
- 최적인 최소값을 찾는 것이 다른 방법들에 비해 굉장히 어려움