경사하강법 (Gradient Descent)

경사하강법은 주어진 수학 함수의 최소값/최대값을 찾는 데 사용되는 반복적인 1차 최적화 방법

※ 수학에서 최적화(optimization)의 의미 : 특정 집합 위에서 정의된 실수값, 함수, 정수에 대해 그 값이 최대나 최소가 되는 상태를 해석하는 문제

머신러닝 및 딥러닝에서는 일반적으로 손실 함수를 최소화하기 위해 사용됨

요구사항

일반적으로 경사하강법 적용을 위해서는 크게 두 가지 요구사항이 있음

• 미분 가능한 함수
  함수에 불연속인 지점, 뾰족한(좌미분계수, 우미분계수가 다른 점) 지점에서는 미분 불가능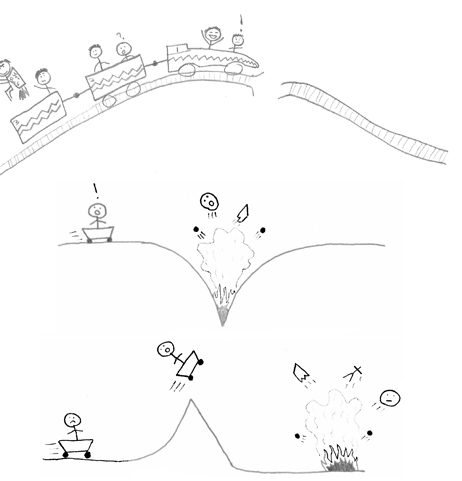

  

• 볼록한(Convex) 함수
  하나의 변수를 갖는 일변량 함수의 경우 함수 내 임의의 두 점을 연결하는 선이 함수 곡선을 교차하지 않으며, 그 선이 곡선보다 위에 있는 함수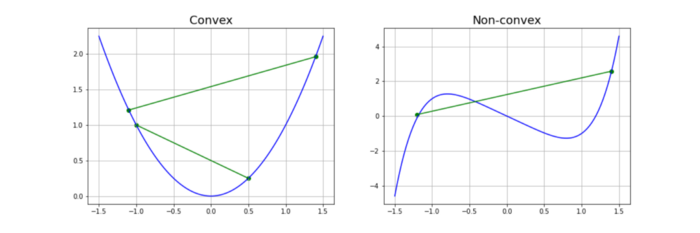

  

일변량함수가 볼록한지 아닌지 수학적으로 확인하는 방법

2차 도함수를 계산하고 그 값이 항상 0보다 큰 지 확인 (크면 볼록, 작으면 오목)
(여기서 볼록은 최소값을 갖는 형태, 오목은 최대값을 갖는 형태로 이해)
(Convex & Concave)

함수 그려주는 사이트

ex)
$f(x)=x^2-x+3$

$f'(x)=2x-1$
$f''(x)=2$

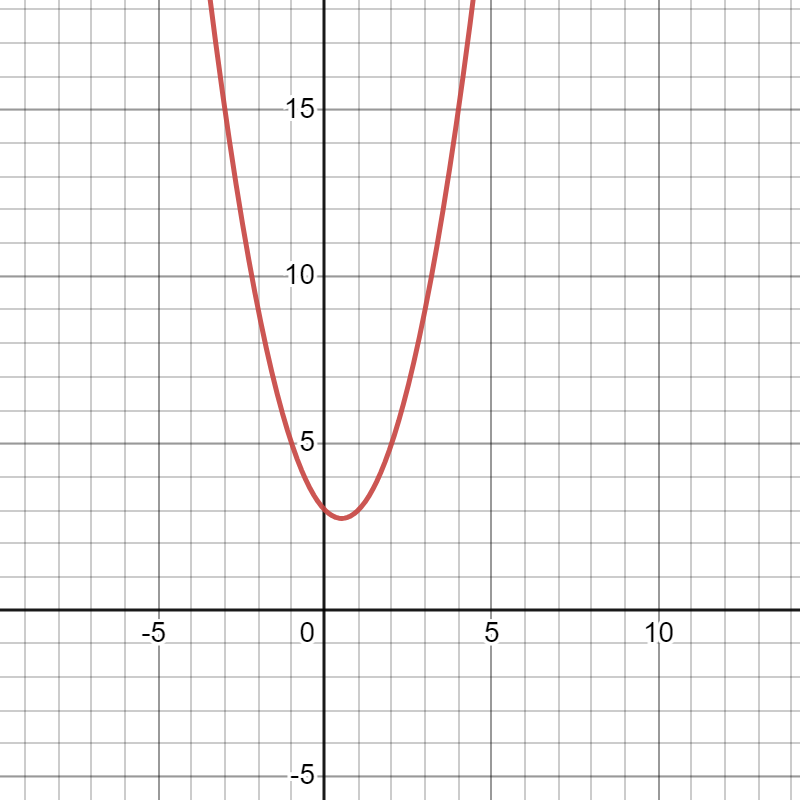
※ 준 볼록 함수를 사용하는 것도 가능하나 종종 알고리즘이 중단될 수 있는 안장점이 있음

$f(x)=x^4-2x^3+2$

$f'(x)=4x^3-6x^2$
$f''(x)=12x^2-12x$

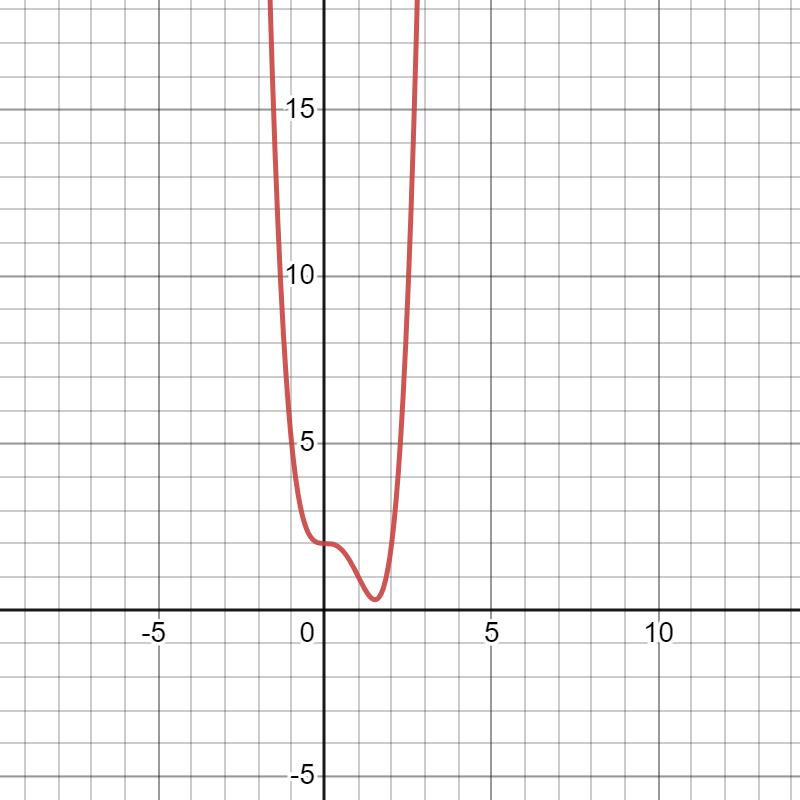
$x$가 0, 1.5일 경우 1차 도함수가 0 (임계점)
$x$가 0, 1일 경우 2차 도함수가 0 (변곡점)

부연 내용

※ 임계점 : 함수의 도함수가 0이 되는 점, 극대점, 극소점, 안장점으로 분류됨

• 극대값 조건 : 2차 도함수가 0보다 큰 경우
• 극소값 조건 : 2차 도함수가 0보다 작은 경우
• 안장점 조건 : 2차 도함수가 0인 경우 (극대인지 극소인지 모호)

※ 변곡점 : 곡선이 오목에서 볼록으로, 볼록에서 오목으로 변하는 지점

위 함수는 $x<0$일 때 볼록, $0<x<1$일 때 오목, $x>1$일 때 다시 볼록한 함수

일단 위 값들을 근거로 해당 함수의 극값 후보인 $x$는 0과 1.5이며, 0인 경우 안장점, 1.5인 경우 2차 도함수가 0보다 작은 유일한 극값 후보이기에 전역 최소값임

Gradient?

주어진 점에서 곡선의 기울기
일변량함수의 경우 특정 점에서의 1차 도함수
다변수함수의 경우 각 주요 방향의 도함수 벡터
ex)
$f(x,y)=0.5x^2+y^2$

점 (10,10)에서의 기울기

$x$에 대한 도함수 = $x$
$y$에 대한 도함수 = $2y$

따라서 10, 10에서의 기울기는 $[10, 20]$으로 볼 수 있음

Gradient Descent

손실 함수를 최소화하는 목적으로 사용할 경우, 해당 함수의 최소값을 찾는 것이 목표

단계

1. 시작점 선택 (초기화)
2. 기울기(gradient) 계산
3. 기울기와 반대되는 방향으로 점을 옮김 (최소화를 목표로 하기 때문에)
4. 기준 중 하나가 충족될 때까지 2번과 3번 항목을 반복

기준

• 최대 반복 횟수 도달
• 허용 오차보다 작을 경우

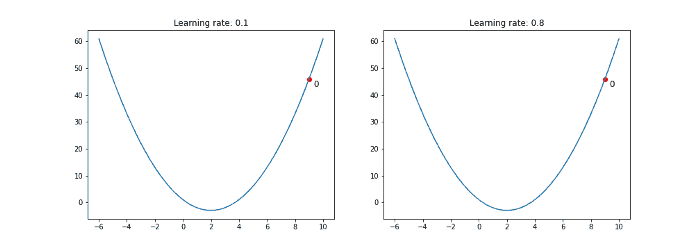
학습률 (learning rate)

위 단계 중 3번인 점을 옮기는 정도
학습률이 작을 경우 최적 지점에 도달할 가능성이 높으나 지역 최소값에 빠지거나, 많은 반복을 필요로 함
학습률이 클 경우 최적의 지점으로 수렴이 불가능할 수 있음

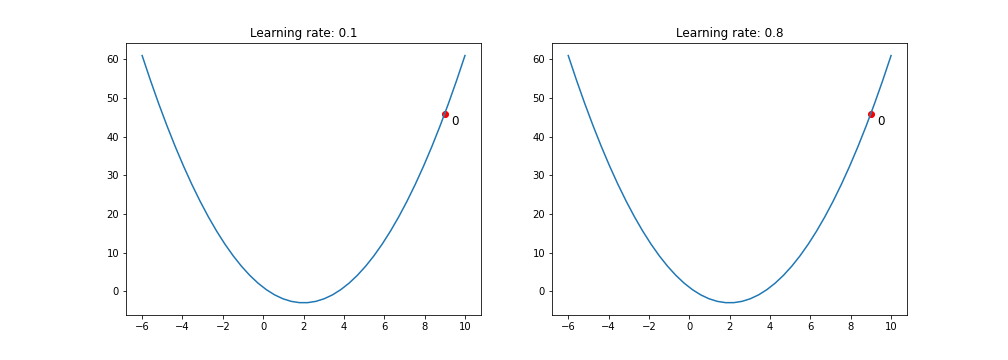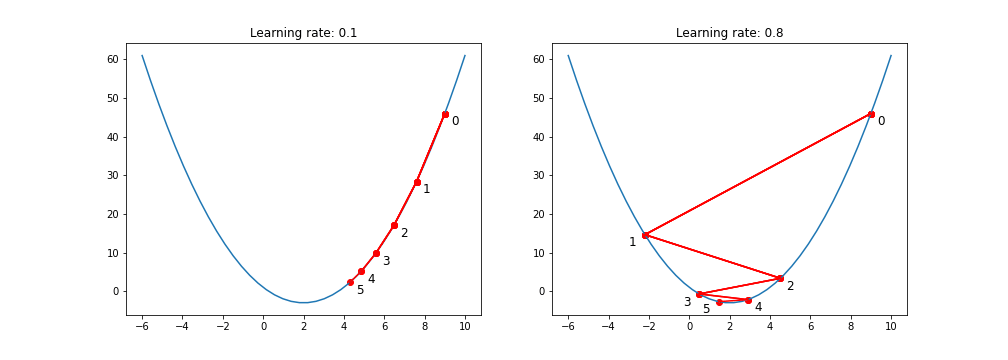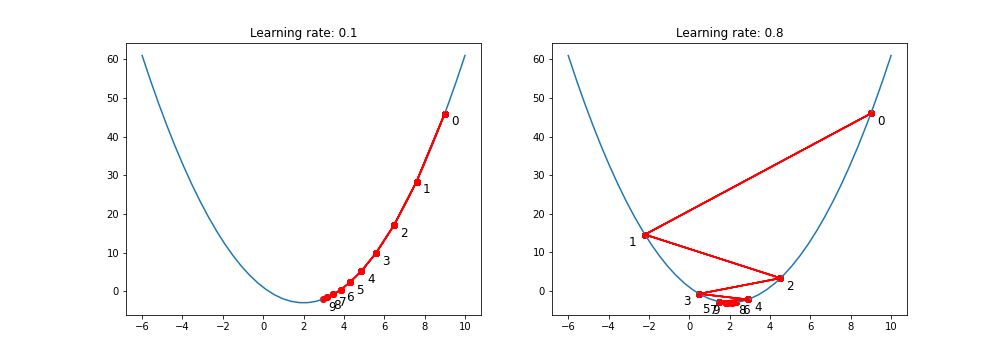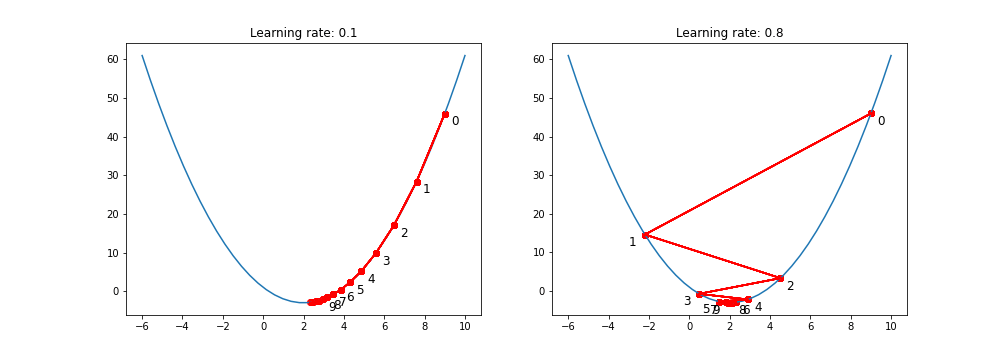
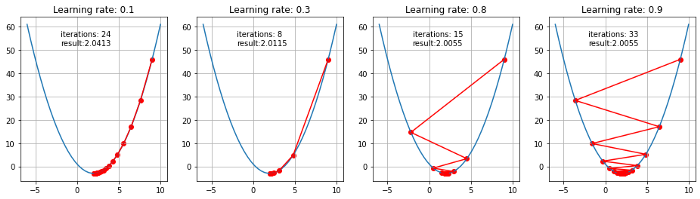
안장점이 있는 함수에서의 Gradient Descent

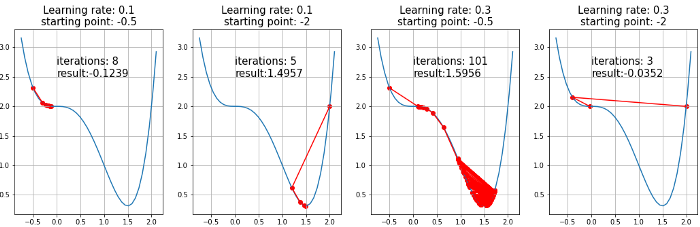
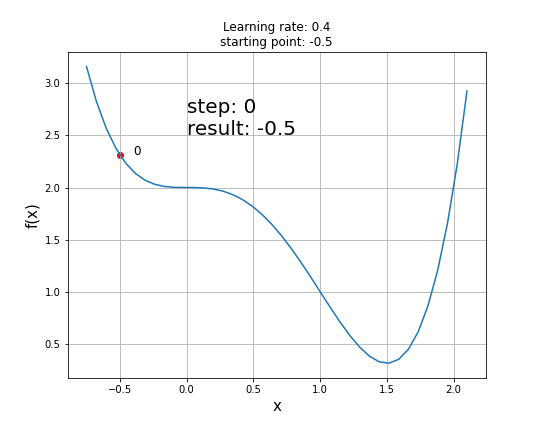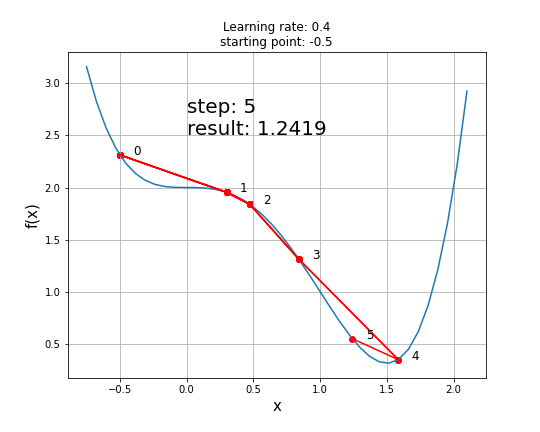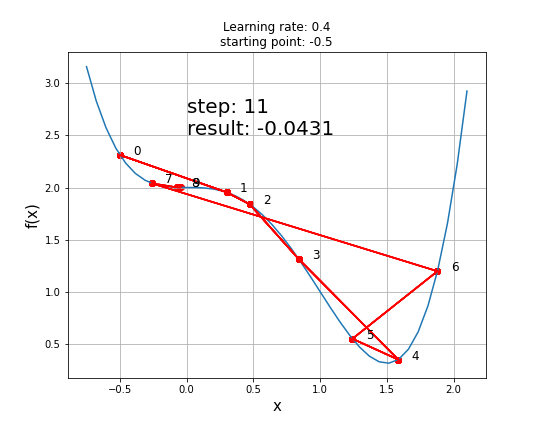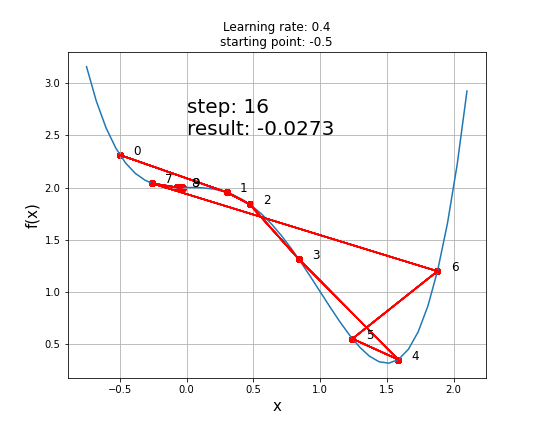
안장점은 Gradient Descent 과정에서 최소값을 찾는데 방해가 될 수 있음

경사 하강법을 수행하기 위한 여러 최적화 알고리즘(optimizer)이 있으며, 손실을 계산하는 손실 함수(loss function)의 종류 또한 다양하다 (추후 다룰 예정)