1. 문제 링크 및 문제
https://www.acmicpc.net/problem/1937
2. 해결 방법 생각해보자 ...
- 판다를 상하좌우로 움직여야 함 ==> DFS
- 숲의 최대 크기가 500 이므로 ==> 시간초과 가능성, DP를 활용하여 불필요한 반복은 줄임.
3. 설명과 코드
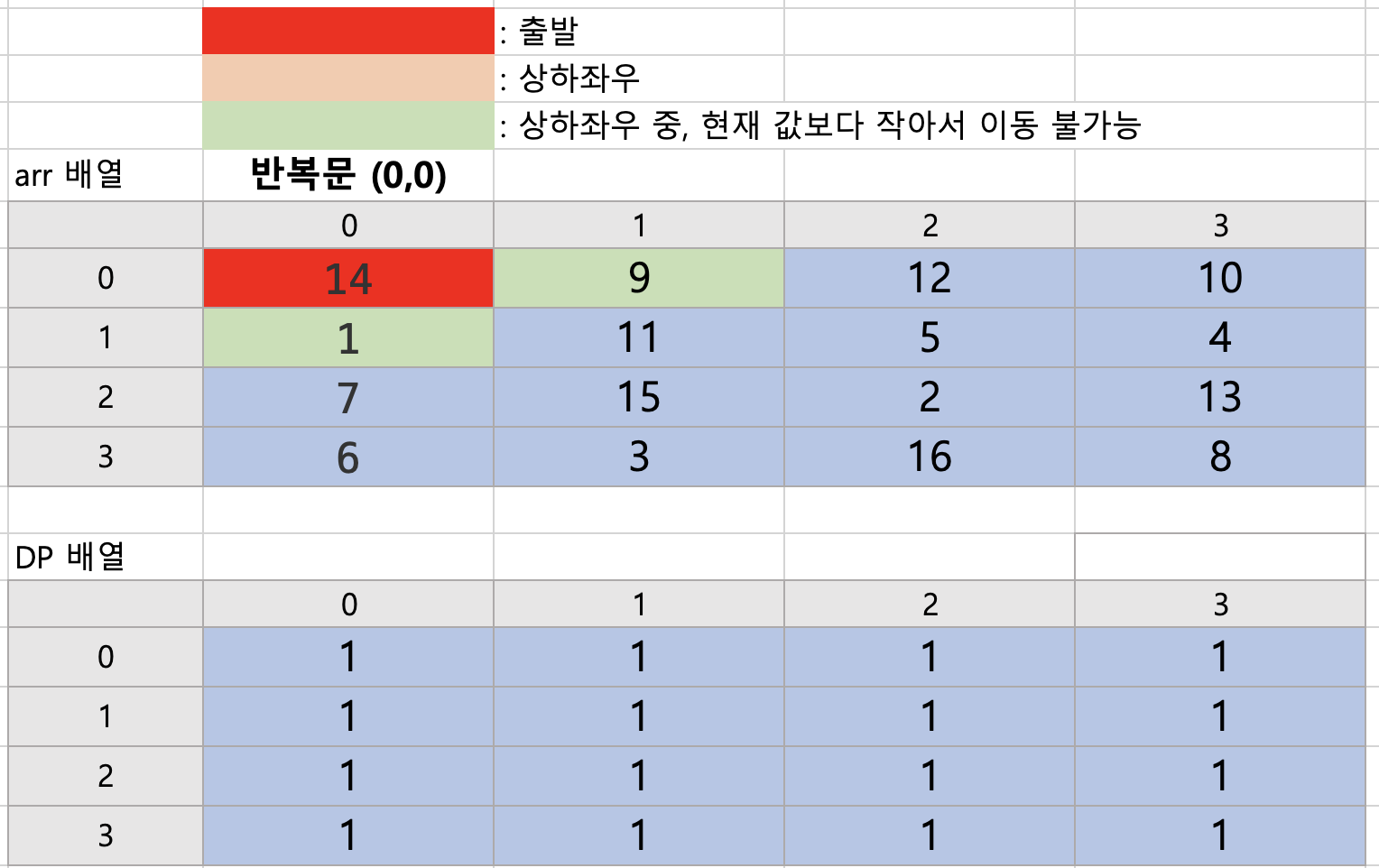
(0,0)~(N,N)까지 탐색하는 반복문에서
1. (0,0)일 때, 상하좌우 중 갈 수 있는 칸 없음.
2. (0,1)일 때, 좌,우,하 가능 => 가능한 영역에서 또 dfs를 실행하여, 최대 영역을 구함
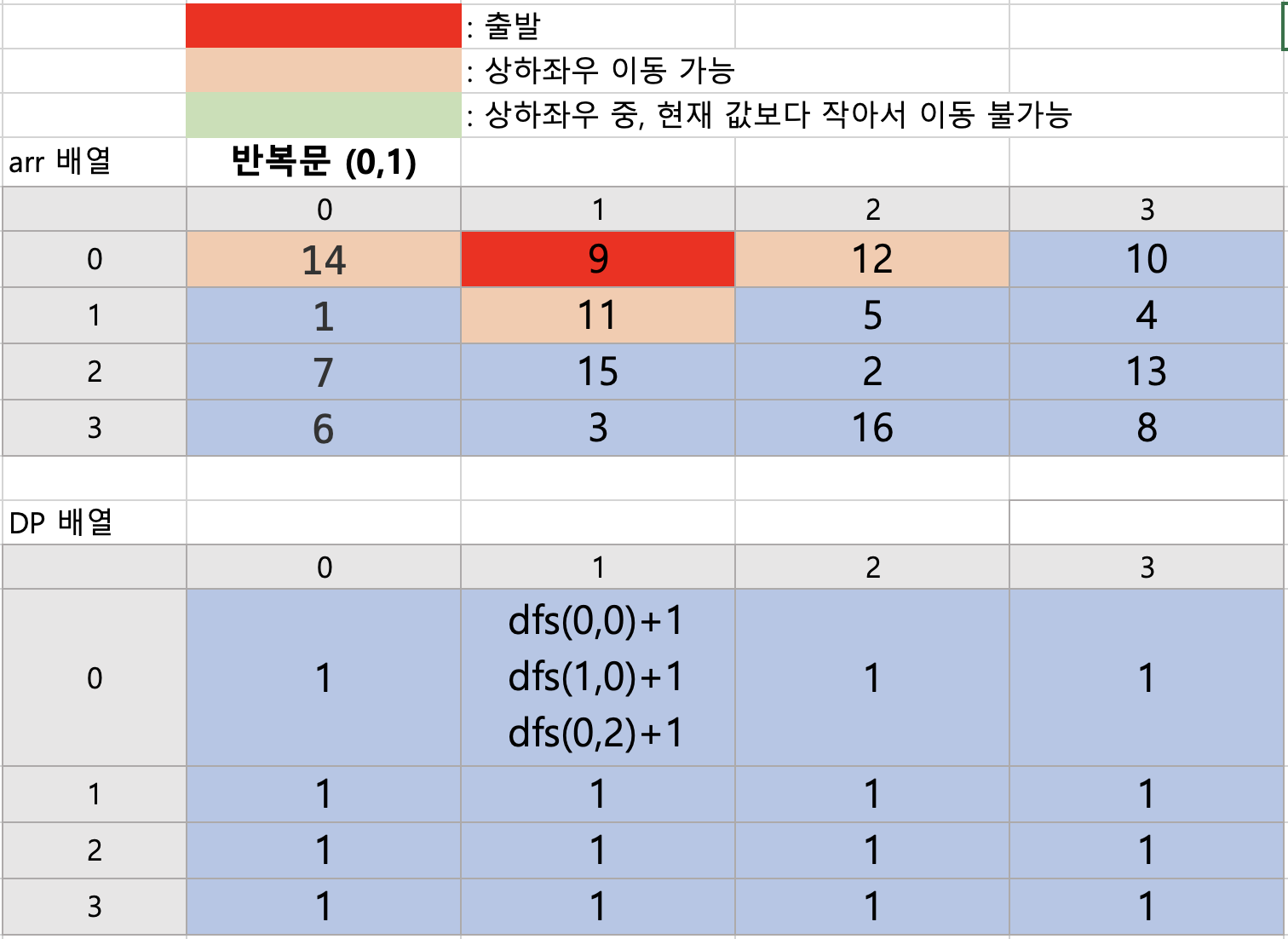
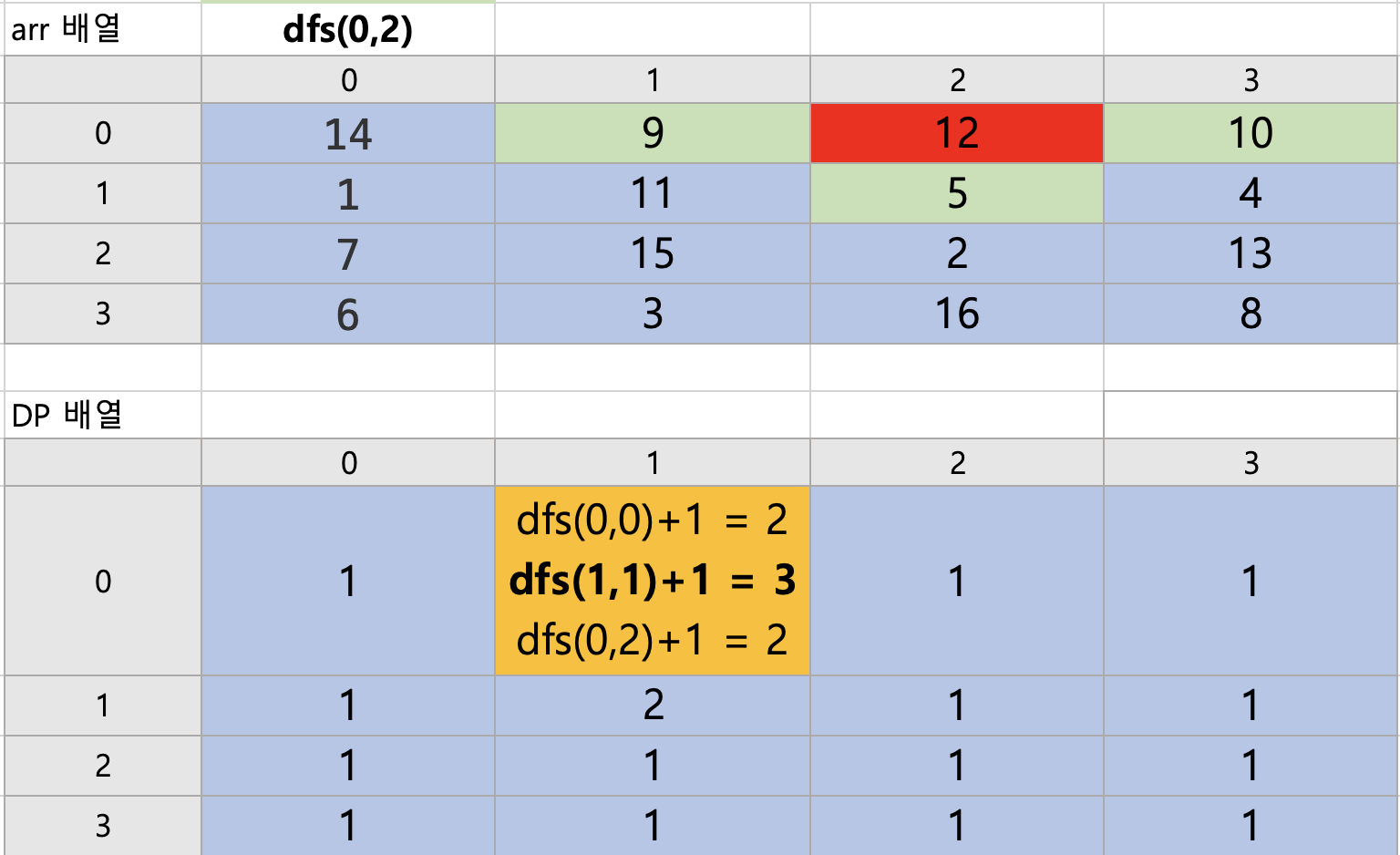
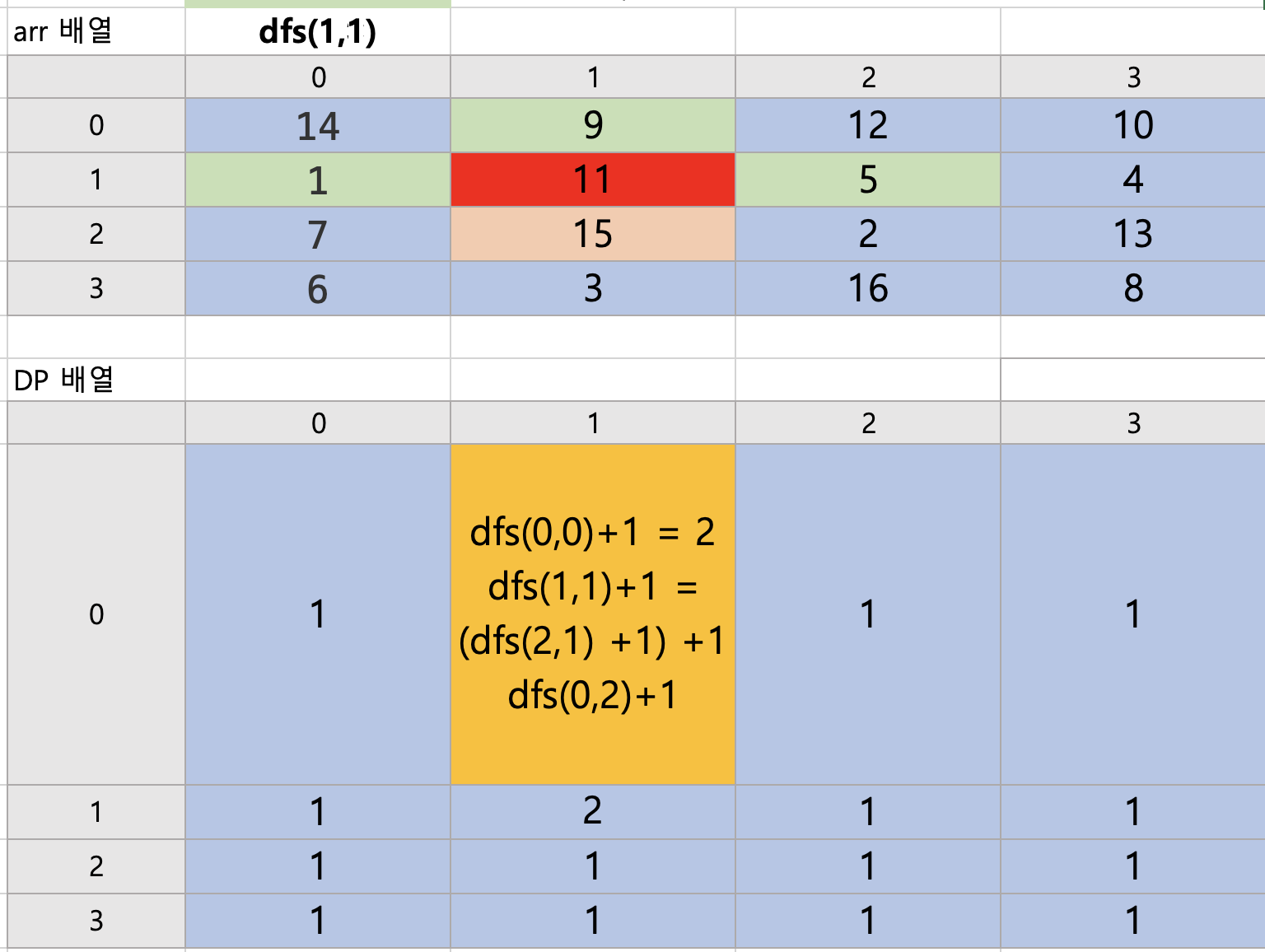
자, 그럼 dfs(0,0), dfs(1,1), dfs(0,2) 차례로 값을 살펴보자.
dfs(0,0)+1 = 2 ( dfs(0,0)은 반복문 제일 처음 과정에서 계산해보았음.)
dfs(1,1) : 2,1 로 이동 가능, dfs(2,1)+1
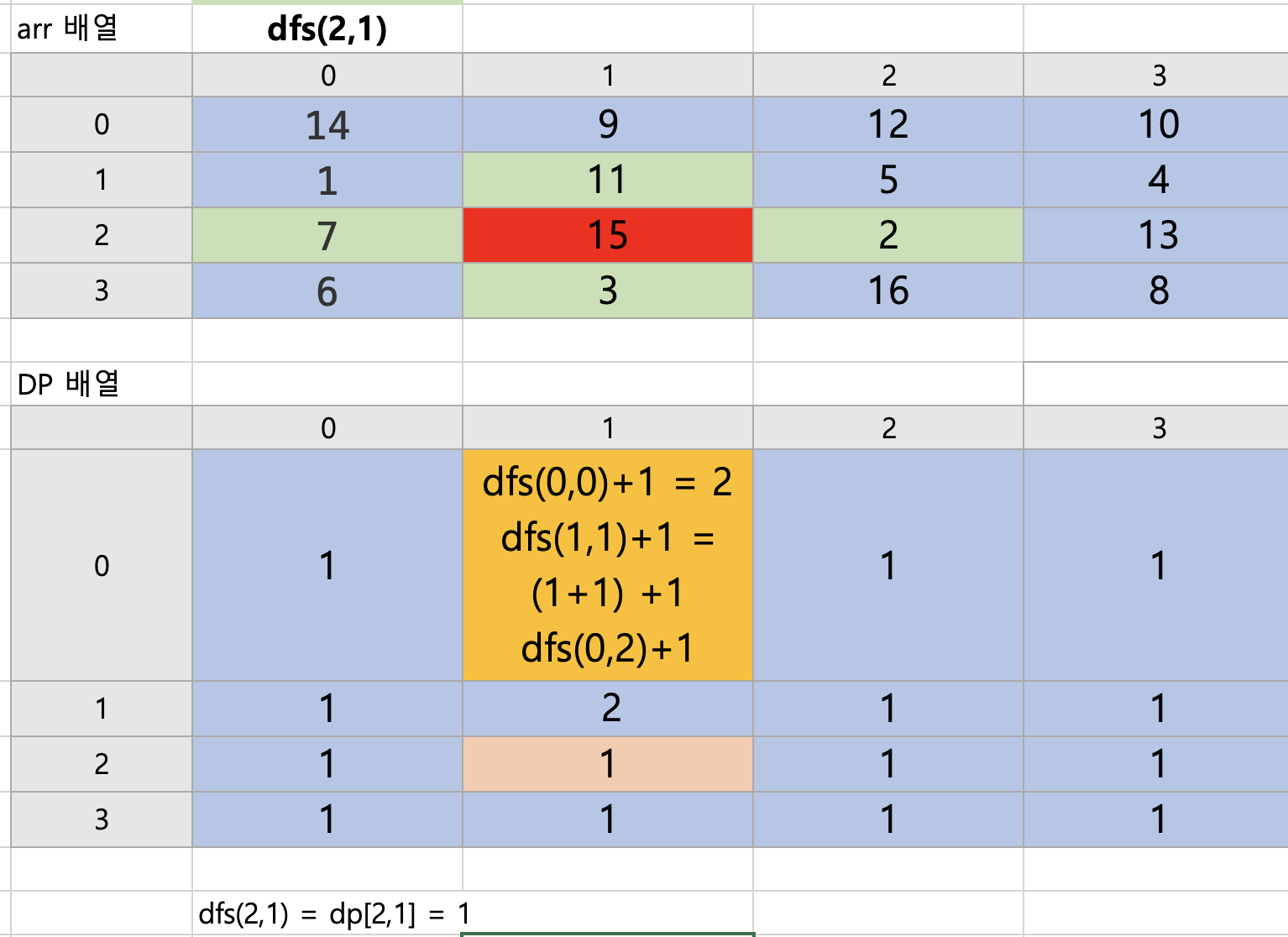
dfs(2,1) : 상하좌우 모두 이동이 불가능하므로 최대경로임 .
dfs(0,2)
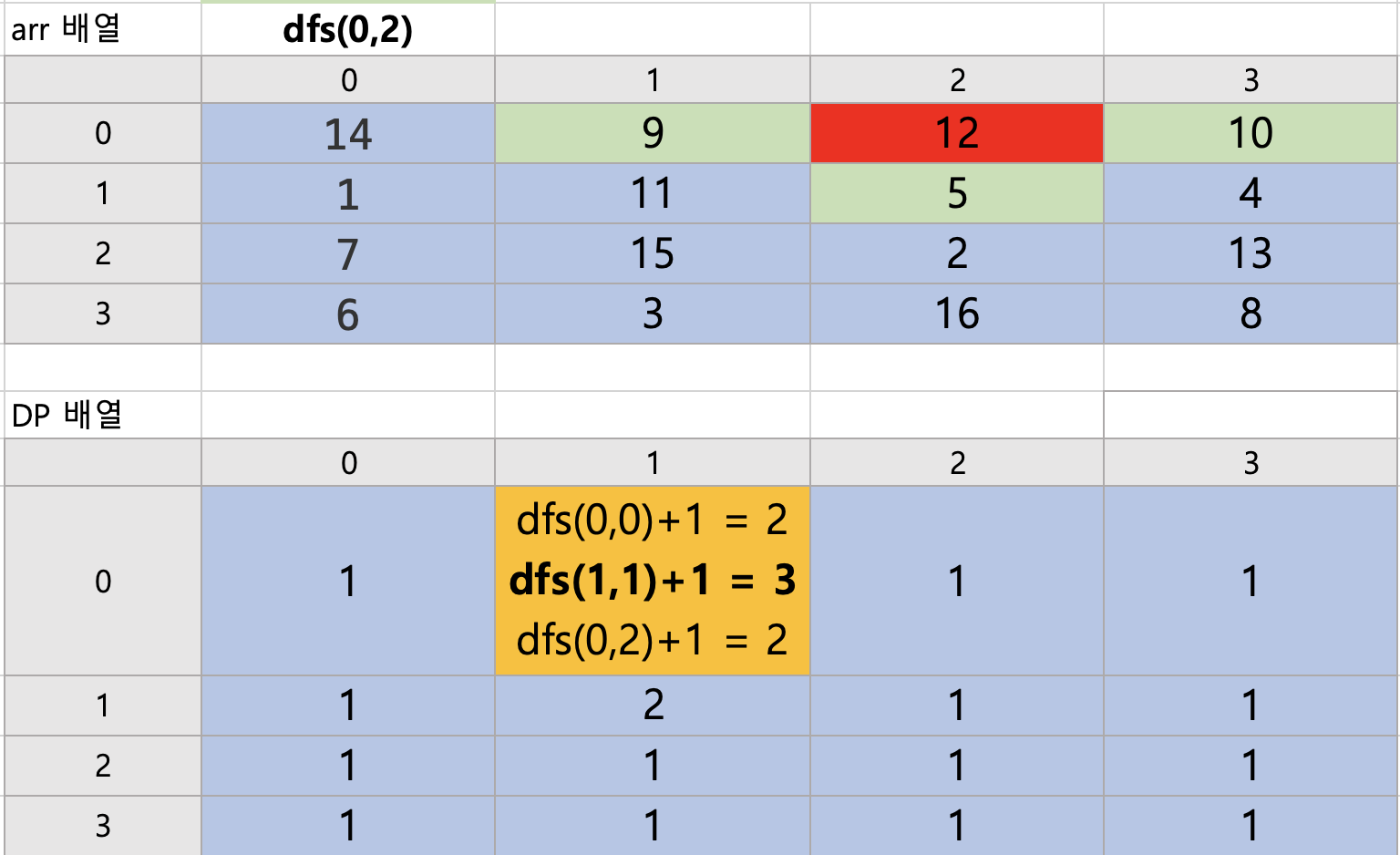
이렇게 하여 반복문 (0,1) 과정 끝.
0,1 좌표의 상하좌우 좌표들이 얻을 수 있는 최대 경로를 구하게 되었으므로,
dp[x][y]가 1이 아니다 = 이미 최대 경로가 구해져있다 이 말씀.
이를 다음 계산 때 활용하려면 dp[x][y] == 1 일 때만 최대 경로 계산!! 하여 시간복잡도 줄임.
import java.io.*;
import java.util.*;
public class Main {
static int N;
static int[][] arr;
static int[][] dp;
static int MaxResult = 0;
static int[] dx = {-1,0,1,0};
static int[] dy = {0,1,0,-1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
arr = new int[N][N];
dp = new int[N][N];
for(int i=0;i<N;i++)Arrays.fill(dp[i],1);
for(int i=0;i<N;i++){
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j=0;j<N;j++){
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
MaxResult = Math.max(MaxResult, dfs(i,j));
}
}
System.out.println(MaxResult);
}
public static int dfs(int x, int y){
for(int k=0;k<4;k++){
int xx = x+dx[k];
int yy = y+dy[k];
if (xx<0 || xx>=N || yy<0 || yy>=N || arr[x][y] >= arr[xx][yy]) continue;
if(dp[xx][yy] == 1){
dp[x][y] = Math.max(dp[x][y], dfs(xx,yy)+1);
}else{
dp[x][y] = Math.max(dp[x][y], dp[xx][yy]+1);
}
}
return dp[x][y];
}
}