그래프 Graph

그래프

노드와 에지로 구성된 집합.
(트리도 그래프의 일종)

그래프 알고리즘

1. 유니온 파인드(그래프에서 사이클 여부를 파악하는데 사용)
2. 위상 정렬(사이클이 없고, 방향이 있는 그래프, 노드를 정렬하는 문제, 전후관계)
3. 다익스트라(시작점에서 다른 모든 노드로 가는 최단거리 알고리즘, 음수간선X)
4. 벨만 포드(다익스트라와 같음, 음수간선O, 음수사이클 여부 판별하는데 사용, 시간 여행)
5. 플로이드 워셜(시작점이 없고, 모든 노드에 대해서 최단거리 구하는 알고리즘, 시간복잡도 나쁨)
6. 최소 신장 트리(MST, 최소 가중치로 간선을 써서 모든 노드 연결하기, 사이클 없어야 해서 유니온 파인드 필요)

그래프의 표현

(노드 개수 N)

1. 에지 리스트

에지 중심 알고리즘인 벨만 포드, 크루스칼(MST)에 사용 가능

• 가중치 없는 그래프 A[2][N]
• 가중치 있는 그래프 A[3][N]

2. 인접 행렬

노드가 적을 때 사용 가능

• 가중치 없는 그래프 A[N][N] (A[1][2] = 1 or 0)
• 가중치 있는 그래프 A[N][N] (A[1][2] = 4)

3. 인접 리스트

• 가중치 없는 그래프 ArrayList<ArrayList<Integer>>
  
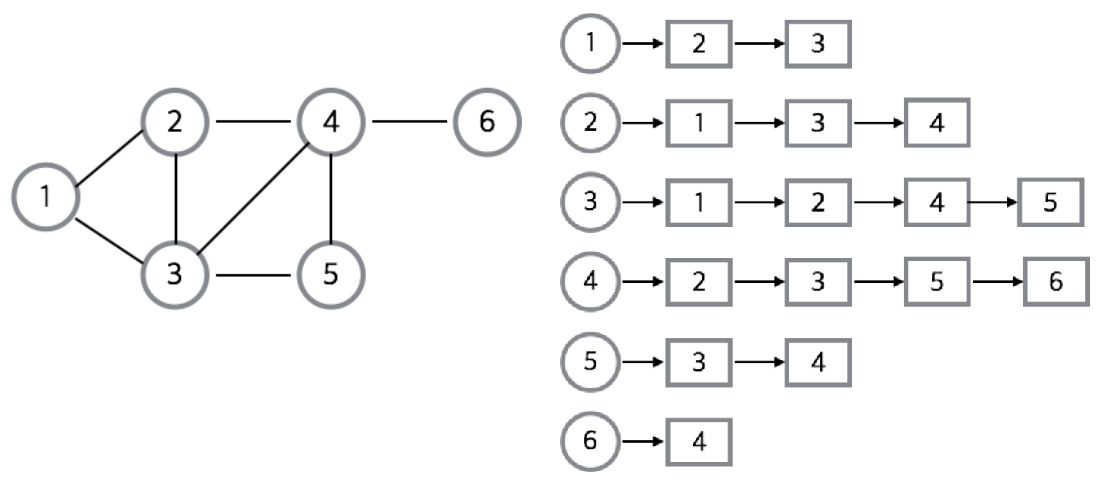
• 가중치 있는 그래프 ArrayList<ArrayList<Node>>
  (가중치 있으면 Node라는 클래스를 만들어서 넣어줘야 함)
  

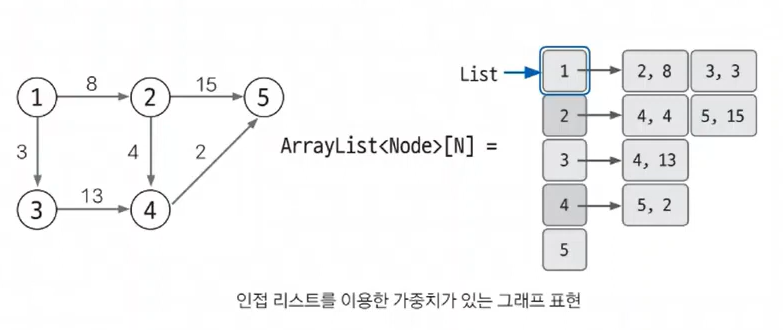
인접 리스트 구현하기

1. 가중치 있는 경우 Node 클래스 생성하기
2. ArrayList 초기화하기
   for (int i = 0; i < V + 1; i++) { graph.add(new ArrayList<Node>()); }
3. 출발 노드를 기준으로 값 삽입 graph.get(x).add(new Node(y, w));
4. 양방향일 경우 출발과 도착 노드 반대로도 삽입
5. 인접 리스트 접근하기 : 해당 노드 x graph.get(x)
   해당 노드 x의 이웃 노드 i graph.get(x).get(i)

(ArrayList<Integer>[] adjacencyList = new ArrayList[node+1];는 타입 안정성이 떨어짐)

인접 리스트 코드

import java.util.ArrayList;
import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		int V = sc.nextInt();
		int E = sc.nextInt();
		
		// 인접 리스트
		ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
		
		// 초기화
		for (int i = 0; i < V + 1; i++) {
			graph.add(new ArrayList<Node>());
		}
		
		int x, y, w;
		for (int i = 0; i < E; i++) {
			x = sc.nextInt();
			y = sc.nextInt();
			w = sc.nextInt();
			// 단방향
			graph.get(x).add(new Node(y, w));
		}
		
		System.out.println(graph);
		
		
	}

	public static class Node {
		int end;
		int weight;

		public Node(int end, int weight) {
			this.end = end;
			this.weight = weight;
		}
		
		@Override
		public String toString() {
			return "[" + end + ", " + weight + "]";
		}

	}

}

(구현이 복잡하지만 시간복잡도와 공간 효율 좋음, 노드 중심 알고리즘에 유용.)

그외 - 연결 요소(Connected Component)란?

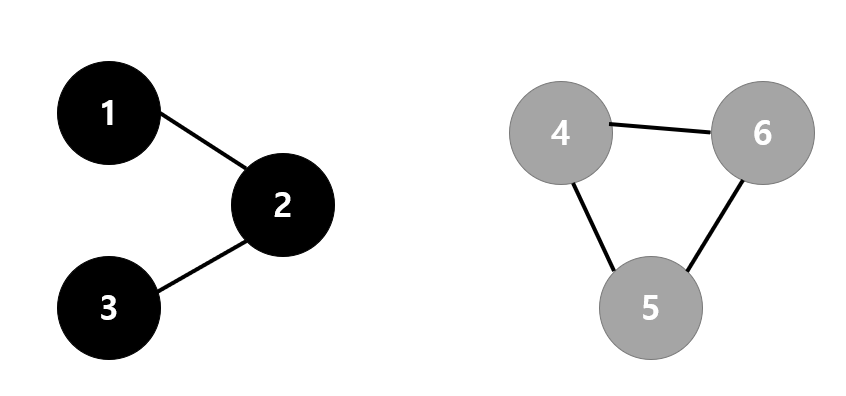위의 사진은 그래프는 하나, 연결 요소는 2개이다.

(DFS, BFS는 가중치 없는 그래프 탐색)