이진 탐색/이분 탐색

백준 1920 실버4
백준 2110 골드4

이진 탐색

: 데이터가 정렬되어 있는 상태에서 원하는 값을 찾아내는 알고리즘
시간 복잡도 O(logn)

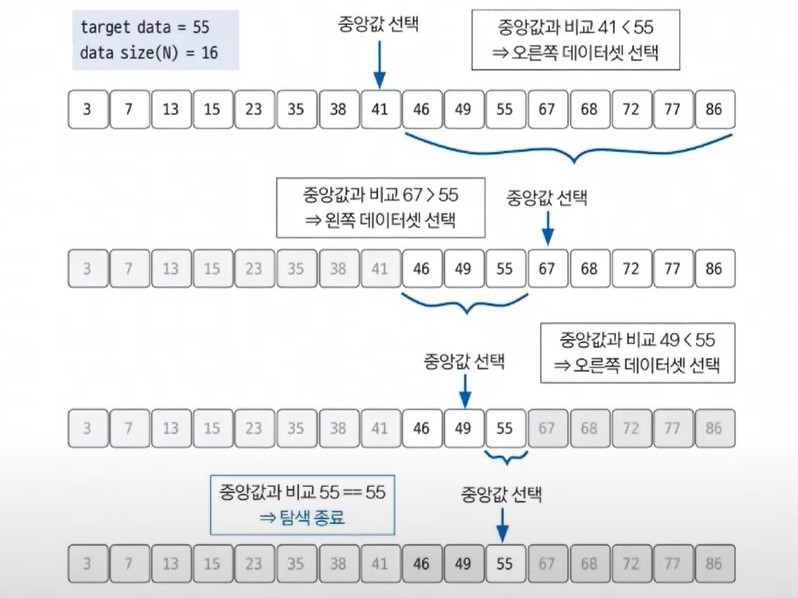
이진 탐색 과정

정렬된 데이터에서

1. 현재 데이터셋의 중앙값을 선택
2. 중앙값 > 타깃 데이터일 때 중앙값 기준으로 왼쪽 데이터셋을 선택
3. 중앙값 < 타깃 데이터일 때 중앙값 기준으로 오른쪽 데이터셋을 선택
4. 1 2 3을 반복하다가 중앙값 == 타깃 데이터일 때 종료

백준 1920

import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

        int[] arr = new int[N];
        StringTokenizer st = new StringTokenizer(br.readLine());
        for(int i=0;i<N;i++){
            arr[i] = Integer.parseInt(st.nextToken());
        }
        Arrays.sort(arr);

        int M = Integer.parseInt(br.readLine());

        int[] target = new int[M];
        st = new StringTokenizer(br.readLine());
        for(int i=0;i<M;i++){
            target[i] = Integer.parseInt(st.nextToken());
        }

        for(int i=0;i<M;i++){
            int start = 0;
            int end = arr.length - 1;
            boolean find = false;
            while(start<=end){
                int mid = (start+end)/2;
                if(arr[mid]>target[i]){
                    end = mid-1;
                }else if(arr[mid]<target[i]){
                    start = mid+1;
                }else{
                    System.out.println("1");
                    find = true;
                    break;
                }
            }
            if(!find){
                System.out.println("0");
            }
        }


    }
}

백준 2110

가장 인접한 두 공유기 사이의 최대 거리라는 건 최대한 공유기를 공평하게 떨어뜨려 놓아야 함을 의미한다.

1. 1654번과 비슷하게 구하고자 하는 '가장 인접한 두 공유기 사이 최대 거리'를 이분탐색 대상으로 둔다.

2. mid를 통해 설정한 거리를 이용해 공유기를 설치하는데 설치 방법은 mid 거리보다는 무조건 크거나 같아야 한다. 일단 공유기의 개수와 상관없이 설치를 한다. 이때 첫번째 집은 조금이라도 공유기 사이 최대 거리를 줄이기 위해 무조건 설치한다.

3. 설치 후 사용된 공유기의 개수를 봤을때

• 조건인 C개보다 큰 경우(같은 경우도): 현재 mid에 따라 설치한 공유기 중 몇개를 빼고 조금 더 띄엄띄엄 설치할 수 있다는 거다. 그러므로 최대 거리는 아니지만 문제의 조건에 성립한다. 최대 거리를 구해야 하므로 값을 저장하고 start값을 늘려준다.
• C개보다 작은 경우: 공유기를 다 설치하지 못했으므로 더 추가해 더 촘촘하게 설치해야 한다는 거다. 그래서 공유기를 해당 mid값으로는 다 설치할 수 없으므로 mid를 무조건 줄여야 한다.

import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    public static int[] house;
    public static int N,C;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        C = Integer.parseInt(st.nextToken());

        house = new int[N];

        for(int i=0;i<N;i++){
            house[i] = Integer.parseInt(br.readLine());
        }
        Arrays.sort(house);

        System.out.println(binarySearch());

    }

    public static int binarySearch(){

        int start = 1;
        int end = house[N-1]-house[0]; // 가장 떨어진 두 집의 거리

        int mid = 0;
        int result = 0;
        while(start <= end){
            mid = (start + end)/2;

            if(install(mid)){
                start = mid + 1;
                result = mid;
            }else{
                end = mid - 1;
            }

        }
        return result;

    }

    public static boolean install(int mid){
        int needRouter = 1;
        int lastHouse = house[0];
        for(int i=1;i<N;i++){
            if(house[i] - lastHouse>= mid){
                needRouter++;
                lastHouse = house[i];
            }
        }

        if(needRouter>=C) {
            return true;
        }
        return false;
    }

}