자료구조

그래프(Graph)

그래프 개념

연결 관계가 있는 데이터를 저장하는 자료 구조

앞-뒤(선형) 관계가 있는 데이터는 배열, 링크드 리스트를 사용한다.
상-하(계층) 관계가 있는 데이터는 트리를 사용한다.

그래프는 연결 관계를 갖는 데이터를 저장하는 자료구조이며, 목적지를 향한 경로나 사회관계망 등의 데이터가 연결 관계를 갖는다. 이러한 데이터를 표현하기 위해서 그래프를 사용한다.

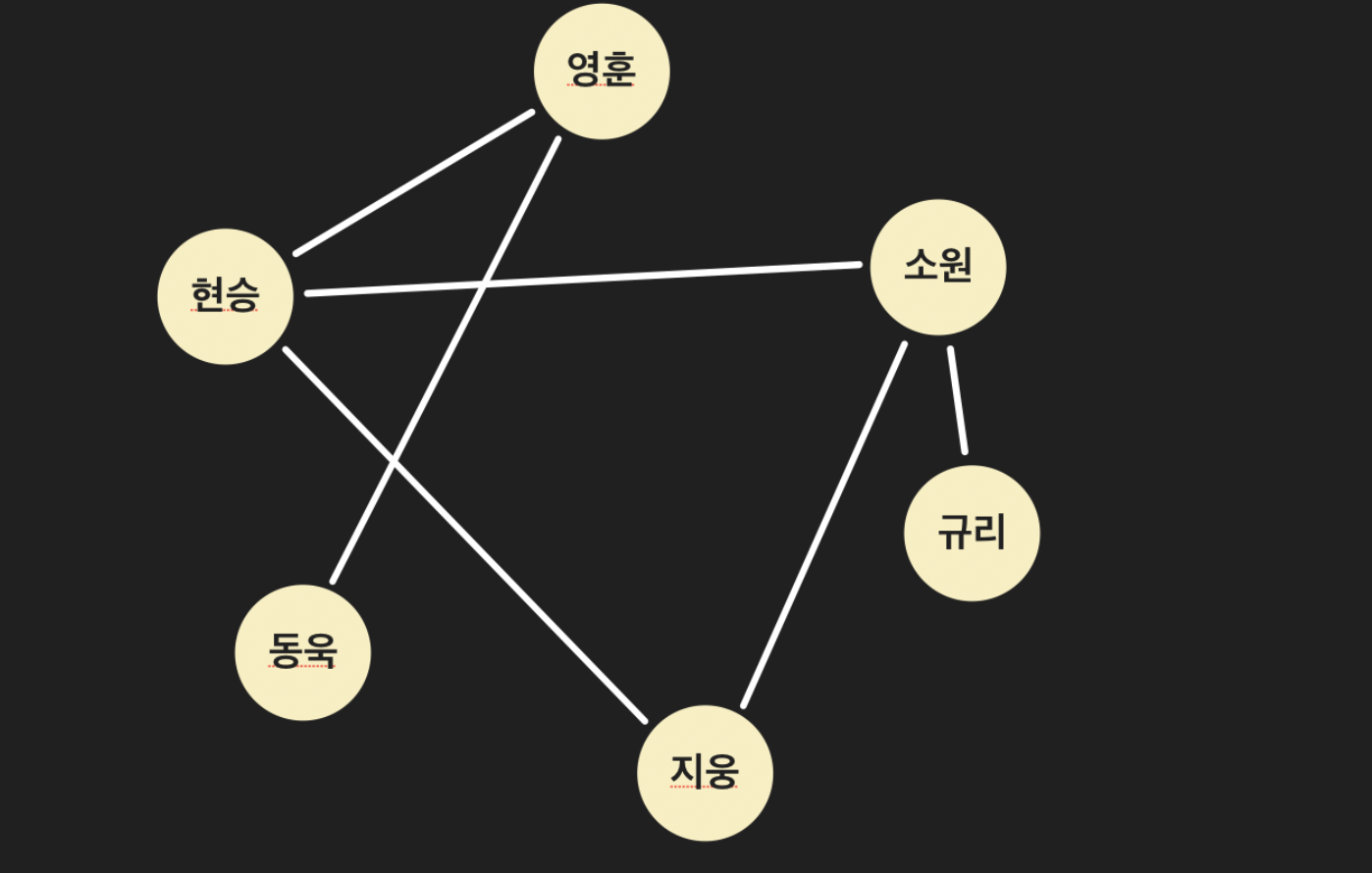
• 노드: 그래프에서 하나의 데이터 단위를 나타내는 객체. SNS 그래프에서는 하나의 유저가 하나의 노드이다. 위 그래프에서는 노란색 원이 노드를 나타낸다.

• 엣지: 그래프에서 두 노드의 직접적인 연결 관계 데이터. 예를 들어, 페이스북 유저 그래프에서는 두 유저의 친구 관계에 해당하는 데이터이다. 위 이미지에서는 흰 선들이 그래프의 엣지에 해당한다. 두 노드 사이에 엣지가 있을 때, “두 노드는 인접해 있다” 라고 표현하며, 엣지가 갖는 특성에 따라 그래프의 종류가 나뉜다.

  • 방향 그래프 (directed graph): 방향 그래프에서는 엣지들이 방향을 갖는다. 인스타그램의 팔로우 관계처럼 한 유저가 다른 유저를 팔로우하는 일방적인 관계를 나타낼 수 있게 해준다.
  • 가중치 그래프 (weighted graph): 가중치 그래프에서는 엣지들이 연결 관계뿐만 아니라 어떤 정보를 나타내는 수치를 가진다. 그 정보는 예를 들자면 친구 관계에서는 친밀도, 위치 정보 그래프면 두 장소 사이의 거리같은 것을 들 수 있다.

• 차수: 하나의 노드에 연결된 엣지들의 수

  • 무방향 그래프에서는 하나의 노드에 연결된 엣지들의 수를 나타내고, 방향 그래프에서는 노드를 떠나는 엣지의 수를 출력 차수, 노드에 들어오는 엣지의 수를 입력 차수로 구별해서 부른다.
  • 위 그래프에서 현승 노드의 차수는 3, 영훈 노드의 차수는 2이다.

• 경로: 한 노드에서 다른 노드까지 가는 길. 지웅 노드와 규리 노드는 서로 인접해 있지 않지만 지웅 노드에서 규리 노드로 갈 수 없는 건 아니다. 지금 지웅과 규리는 둘 다 소원 노드와 친구인데 “지웅 - 소원 - 규리” 이 길을 따라가면 지웅 노드에서 규리 노드로 갈 수 있다. “지웅 - 소원 - 규리” 이런 길을 경로라고 한다.

  • 경로의 거리
    • 비가중치 그래프: 한 경로에 있는 엣지의 수.
    • 가중치 그래프: 한 경로에 있는 엣지의 가중치의 합.
  • 최단 경로: 두 노드 사이의 경로 중 거리가 가장 짧은 경로.
  • 사이클: 한 노드에서 시작해서 같은 노드로 돌아오는 경로.

노드가 서로 연결되어 있는지를 표현할 때, 즉 인접을 표현할 때 두 가지 방법을 사용할 수 있다.

• 인접 행렬
• 인접 리스트

인접 행렬은 리스트 안에 리스트를 통해 행렬 형태로 인접 여부를 표현하는 것이고, 인접 리스트는 노드 객체 안에 인접된 다른 노드를 저장하는 속성을 추가하는 것이다.

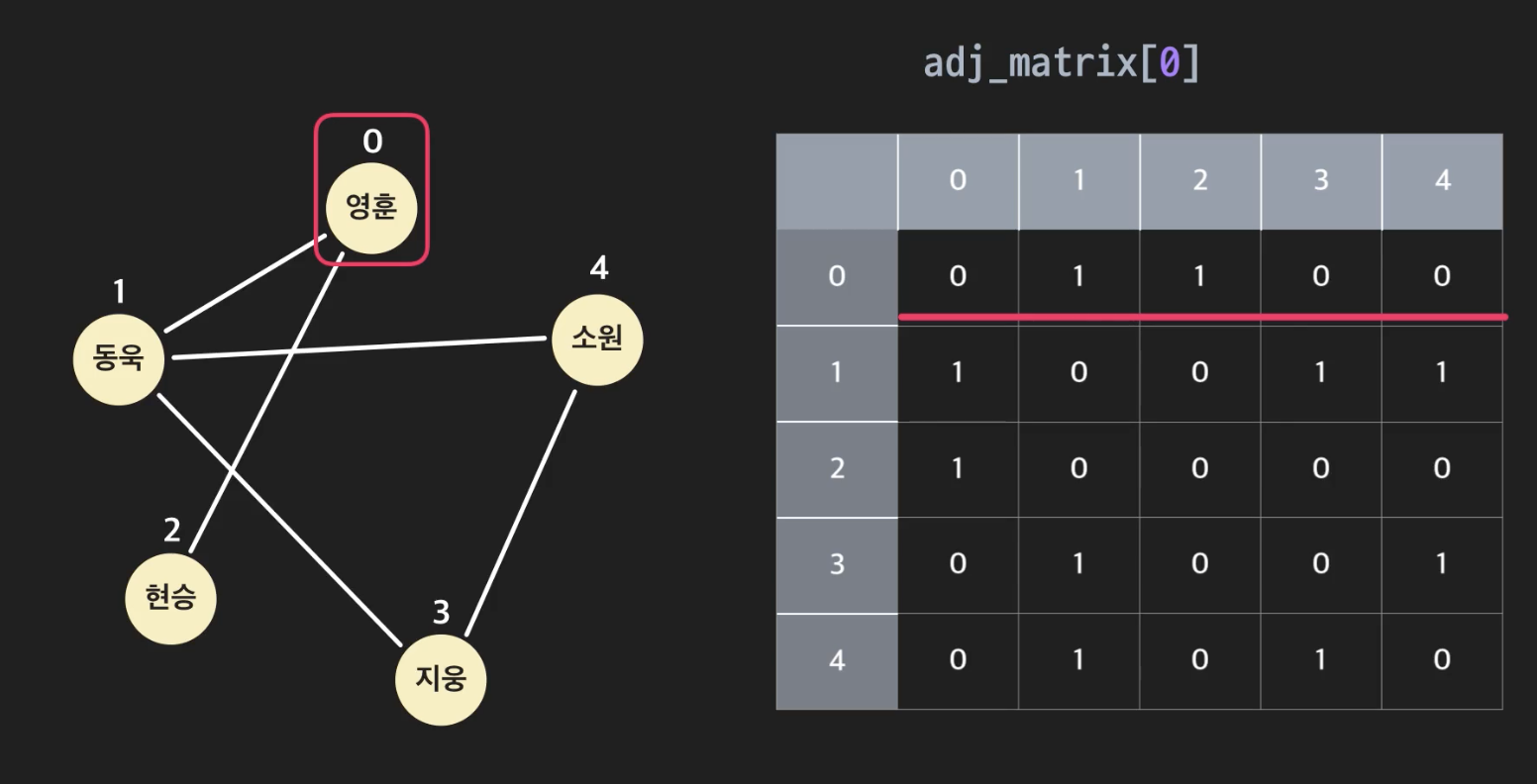
위의 그림이 인접 행렬을 표현한 것이다. 출발점이 되는 노드와 도착점이 되는 노드 간의 인접 여부를 0,1 로 행렬 형태로 표현하였다.

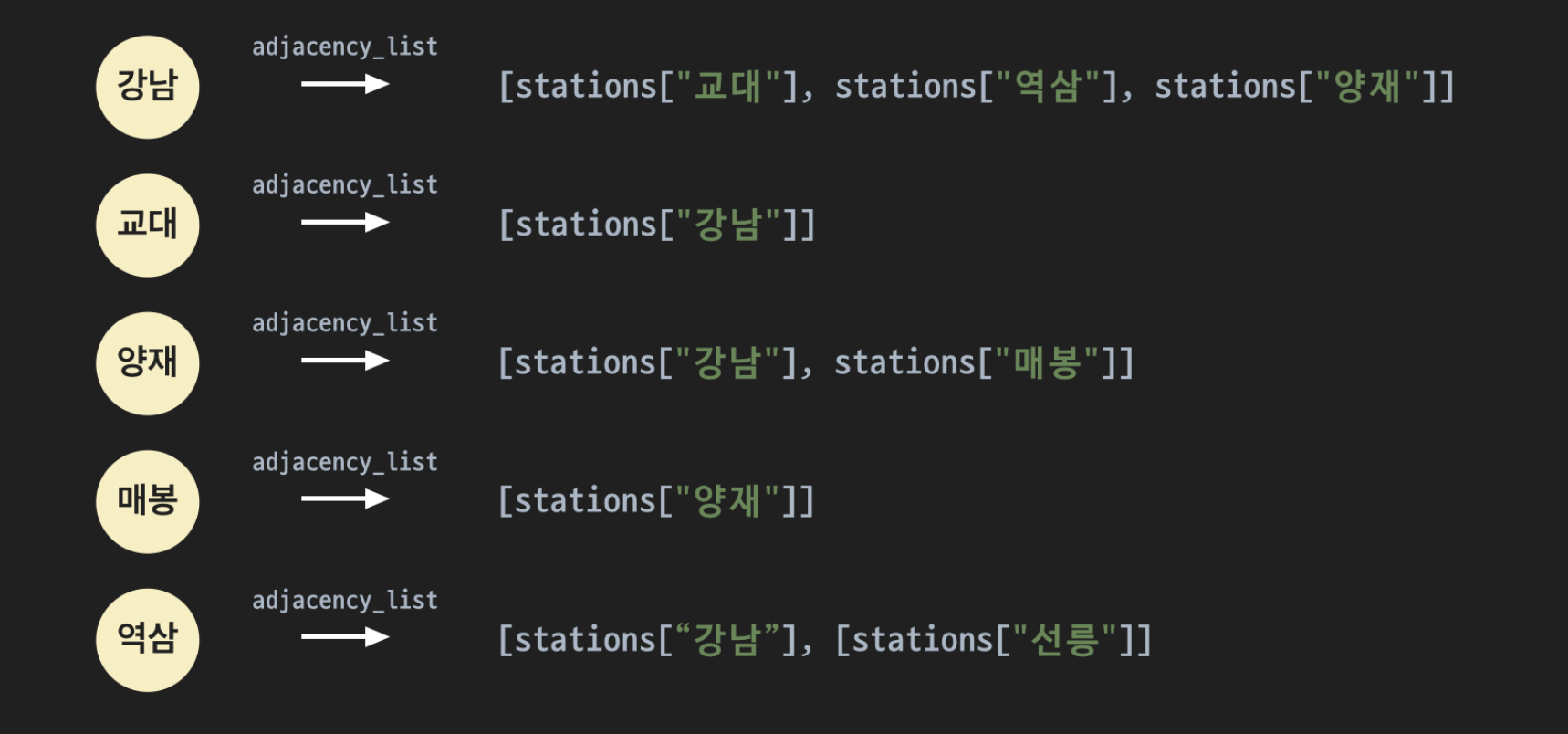
인접 리스트는 그래프 노드 클래스에 인접 리스트를 저장하는 __init__ 속성을 추가하여 위와 같이 중심이 되는 노드에 대한 인접 노드들을 저장한다.

이 때, 인접 리스트는 자신과 인접한 노드들에 대한 레퍼런스를 인접 리스트에 담고 있는 반면 인접 행렬은 본인이 속한 행에 대한 모든 리스트에 접근하여 인접 여부를 확인해야 한다. 따라서, 인접 리스트가 보다 효율적이라고 볼 수 있다.

그래프 탐색

하나의 시작점 노드에서 연결된 모든 노드들을 찾는 것

BFS(Breadth First Search) 알고리즘

너비에 우선하여 탐색한다고 직역할 수 있다.

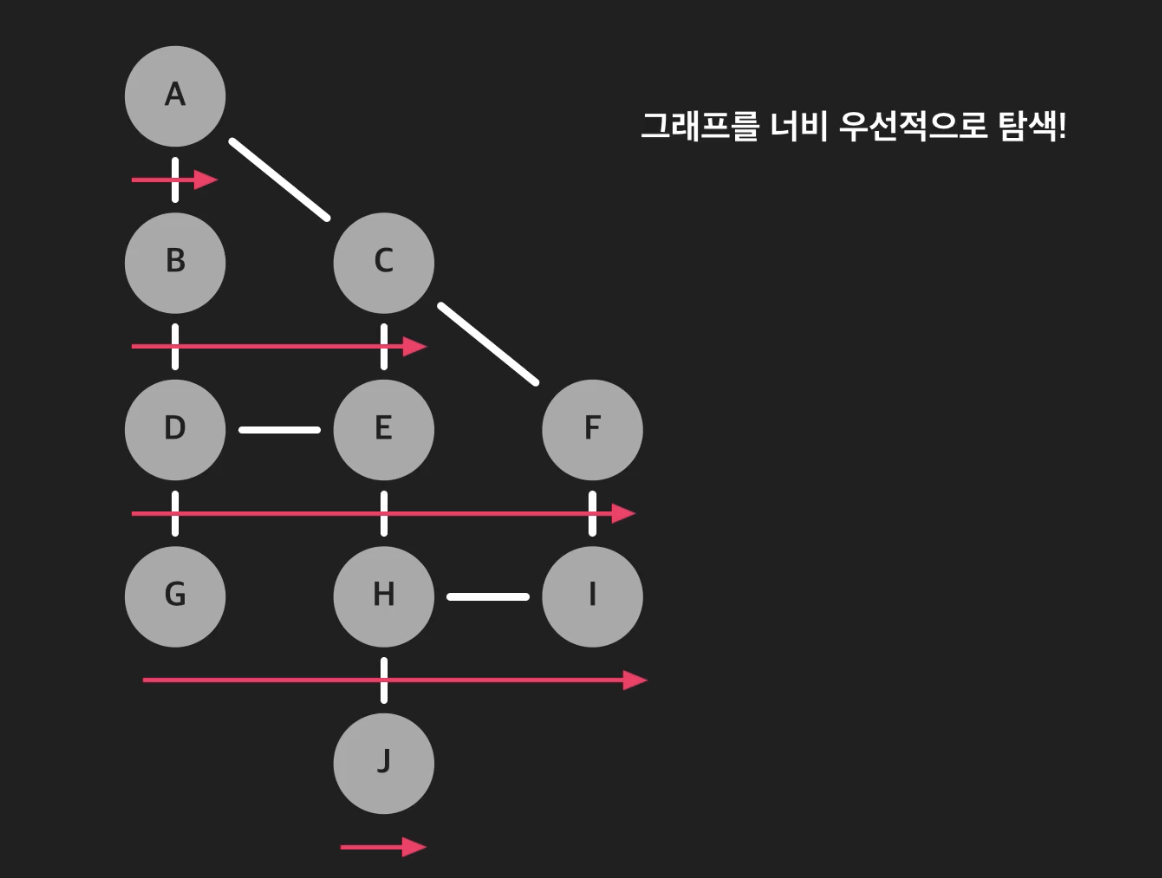
시작점으로부터 밑으로 내려오지만 그 진행 방향이 너비 즉, 가로 방향으로 탐색을 우선하는 방식이다.

BFS 알고리즘에 사용되는 추상 자료형은 바로 큐(Queue)이다. 큐의 큰 특징은 선입선출(FIFO)이다. 시작 노드로부터 가장 가까운 인접노드를 전부 탐색하고 그 다음 노드로 넘어간다. 가장 가까운 노드를 우선하여 탐색하고 그 결과를 저장하기 때문에 선입선출의 큐를 사용한다.

BFS 알고리즘을 일반화하면 다음과 같다.

• 시작점 노드를 방문한 노드 표시 후, 큐에 넣는다
• 큐에 아무 노드도 없을 때까지:
  • 큐에서 가장 앞 노드를 꺼낸다
  • 이 노드에 인접해 있는 노드들을 돌면서:
    • 처음 방문한 노드면:
      • 방문한 노드로 표시한다
      • 큐에 넣는다

코드로 구현하면 아래와 같다.

def bfs(graph, start_node):
    """시작 노드에서 bfs를 실행하는 함수"""
    queue = deque()  # 빈 큐 생성
    # 일단 모든 노드를 방문하지 않은 노드로 표시
    for station_node in graph.values():
        station_node.visited = False
    
    start_node.visited = True
    queue.append(start_node)
    
    while queue:
        current_station = queue.popleft()
        for station in current_station.adjacent_stations:
            if not station.visited:
                station.visited = True
                queue.append(station)

총 노드의 수를 $V$, 엣지의 수를 $E$ 라고 가정한다.

1. 방문하지 않은 모든 노드를 초기화하는데 걸리는 시간 $O(V)$
2. 큐에 노드를 넣고 빼는 시간
   • 파이썬 deque는 더블리 링크드 리스트로 구현되어 있기 때문에 삽입과 삭제에 $O(1)$ 의 시간이 소요된다. $V$개를 수행하는데 $O(V)$가 소요된다.
3. 큐에서 뺀 노드에 인접한 노드들을 도는 시간
   • BFS는 한 번 방문한 노드는 다시 방문하지 않는다. 따라서, 전체 $E$개의 엣지만큼 노드를 돌린다. 시간 복잡도는 $O(E)$ 이다.

모든 단계를 더했을 때, $O(2V+E)$ 의 시간이 소요되며 이는 $O(V+E)$의 시간 복잡도를 갖는다고 볼 수 있다.

DFS(Depth First Search) 알고리즘

BFS와는 달리 너비가 아닌 깊이를 우선하여 탐색하는 알고리즘이다.

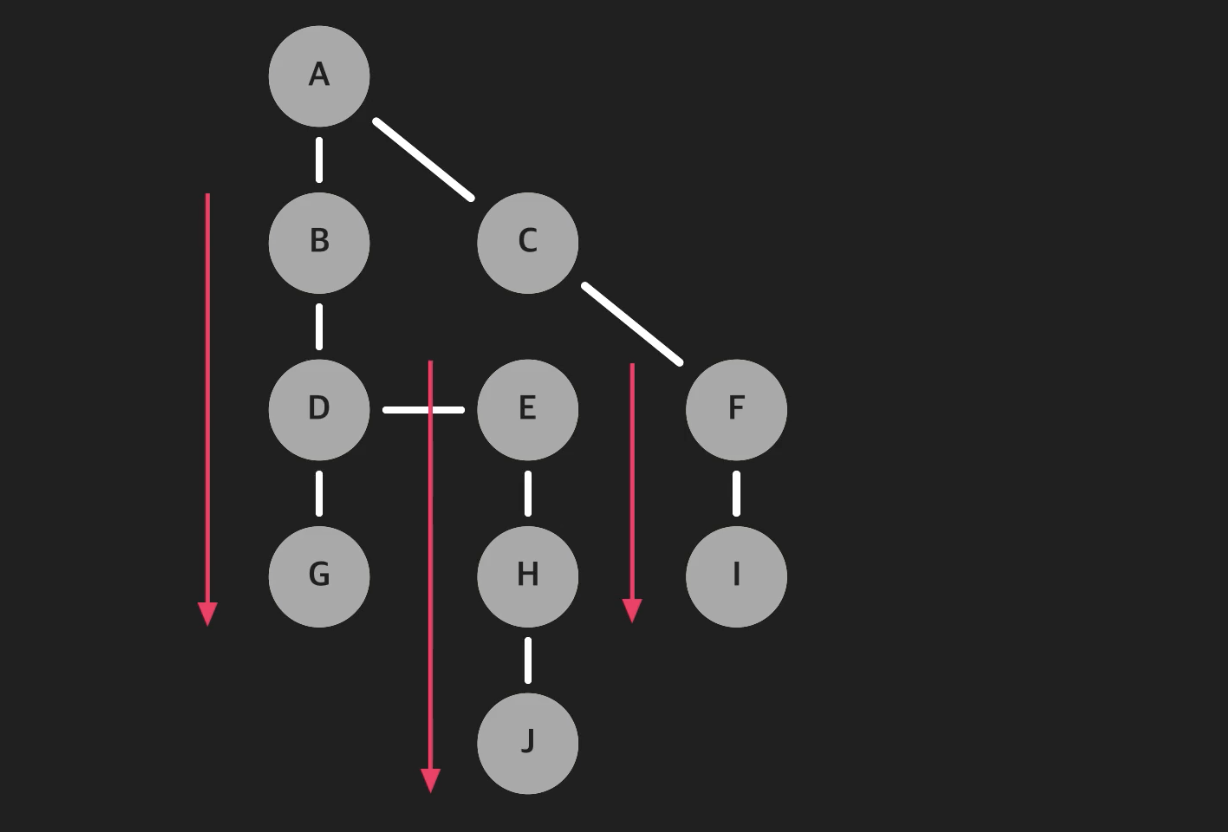
이 때 사용하는 추상 자료형은 스택(stack)이다.

스택은 큐와 반대로 LIFO 즉, 가장 마지막에 저장된 데이터를 가장 먼저 추출하는 특징을 갖는다. DFS 알고리즘은 너비 방향이 아닌 깊이 방향으로 내려가면서 탐색 시작점에서 가장 깊은 노드까지 내려간다. 나중에 저장된 노드가 먼저 처리되는 방식이어야 계속해서 밑으로 내려갈 수 있다. 따라서 스택이 적절하다.

DFS 알고리즘을 일반화하면 다음과 같다.

• 시작점 노드를 방문 표시 후, 스택에 넣는다
• 스택에 아무 노드도 없을 때까지:
  • 스택에서 가장 위 노드를 꺼낸다
  • 이 노드에 인접해 있는 노드들을 돌면서:
    • 처음 방문한 노드면:
      • 방문한 노드로 표시한다
      • 스택에 넣는다

앞서 BFS 알고리즘의 예시로 들었던 코드를 DFS로도 표현해보면 아래와 같다.

def dfs(graph, start_node):
    """최단 경로용 bfs 함수"""
    stack = deque()  # 빈 큐 생성

    # 모든 노드를 처음 보는 노드로 초기화
    for station_node in graph.values():
        station_node.visited = False

    start_node.visited = True
    stack.append(start_node)
    
    while stack:
        last_node = stack.pop()
        for station in last_node.adjacent_stations:
            if not station.visited:
                station.visited = True
                stack.append(station)

이번에도 마찬가지로 노드의 수를 $V$, 엣지의 수를 $E$ 라고 가정했을 때, DFS 알고리즘을 이용한 탐색에 대한 시간 복잡도는 BFS 알고리즘과 동일한 $O(V+E)$이다.
사용되는 추상 자료형과 이를 이용하는 방법의 차이 뿐, 이미 한번 방문한 노드는 다시 방문하지 않는다는 전제가 동일하므로 큰 변화는 없다.

최단 경로 알고리즘

두 노드 사이의 경로가 가장 짧은 경로를 최단 경로라고 하며, 이를 찾는 알고리즘은 다양하지만 그 중에서도 다음 두 가지에 대해서 보자.

• BFS
• DIJKSTRA

BFS

앞서 배웠던 탐색 알고리즘은 BFS 알고리즘을 조금만 수정하면 최단 경로 알고리즘을 구현할 수 있다.
predecessor 라고 하는 직전 경로에 대한 정보만 추가로 저장해주면 된다.
그리고 BFS 알고리즘이 종료된 후에 가장 마지막 노드부터 거꾸로 거슬러 올라가면서 시작점에 도달한다. 이를 Backtracking 이라고 한다.

BFS 알고리즘이 수행되어 시작점으로부터 어떠한 노드에 처음 도착한다. 예컨대 그 거리가 2라고 할 때, 최단경로는 바로 2이다. 만약 1이라면 시작점으로부터 1인 거리에 있는 노드들을 탐색할 때 처음 도착했을 것이기 때문이다. BFS는 너비 방향으로 진행한다. 즉, 시작점으로부터 1인 거리의 노드를 전부 탐색한 후에 거리가 2인 노드들을 탐색하는 방식이다. 따라서 처음 노드에 도착했을 당시 경로를 거슬러 올라간다면 최단 경로가 되는 것이다.
이 때, 그 경로를 저장하고 있는 변수가 바로 predecessor 이다.

BFS 최단 경로 알고리즘을 구현해보자.

def bfs(graph, start_node):
    """최단 경로용 bfs 함수"""
    queue = deque()  # 빈 큐 생성

    # 모든 노드를 방문하지 않은 노드로 표시, 모든 predecessor는 None으로 초기화
    for station_node in graph.values():
        station_node.visited = False
        station_node.predecessor = None

    # 시작점 노드를 방문 표시한 후 큐에 넣어준다
    start_node.visited = True
    queue.append(start_node)
    
    while queue:  # 큐에 노드가 있을 때까지
        current_station = queue.popleft()  # 큐의 가장 앞 데이터를 갖고 온다
        for neighbor in current_station.adjacent_stations:  # 인접한 노드를 돌면서
            if not neighbor.visited:  # 방문하지 않은 노드면
                neighbor.visited = True  # 방문 표시를 하고
                neighbor.predecessor = current_station
                queue.append(neighbor)  # 큐에 넣는다
                
def back_track(destination_node):
    """최단 경로를 찾기 위한 back tracking 함수"""
    res_str = ""  # 리턴할 결과 문자열
    temp = destination_node
    
    while temp is not None:
        res_str = f"{temp.station_name} {res_str}"  # 결과 문자열에 역 이름을 더하고
        temp = temp.predecessor 
    
    return res_str

predecessor 를 최초 초기화한 뒤에 큐에 저장된 노드가 하나씩 꺼내질 때마다 그 때 당시의 노드를 predecessor 에 저장한 뒤, 다음 노드로 넘겨주는 방식이다.
BFS가 종료되면, Backtracking 하여 최종 경로를 찾는다.

Dijkstra

앞선 BFS 알고리즘은 가중치 그래프에서는 사용할 수 없다. 가중치 그래프에서 사용하는 알고리즘이 dijkstra이다.

Dijkstra 알고리즘에 사용되는 변수는 세 가지다.

• distance
• predecessor
• complete

먼저 distance는 특정 노드까지의 최단 거리 예상치를 저장한다. 현재까지 알고 있는 정보를 기반으로 한 예상치다. 만약 탐색의 과정에서 더 짧은 경로가 나타나면 그 때 distance를 업데이트 한다.
predecessor 변수는 현재까지 찾은 최단 경로에 대한 직전 경로를 저장한다. 마찬가지로 더 짧은 경로가 나타나면 이 값도 업데이트 한다.
마지막 complete는 모든 탐색이 종료되고, 노드가 완전히 파악돼었을 때 True로 설정한다.

노드를 하나씩 방문하면서 변수를 업데이트하는 것을 relax 한다고 표현한다.

Dijkstra 알고리즘을 일반화하면 아래와 같다.

• 시작점의 distance를 0으로, predecessor를 None으로 설정한다.
• 모든 노드가 complete 일 때까지:
  • complete 하지 않은 노드 중 가장 distance가 작은 노드 선택
  • 이 노드에 인접해 있는 노드들 중 complete 되자 않은 노드를 돌면서:
    • 각 엣지를 relax한다
  • 현재 노드를 complete 처리한다.