알고리즘 연습

선형탐색

def linear_search(element, some_list):
    for idx, num in enumerate(some_list):
        if element == num:
            return idx

print(linear_search(2, [2, 3, 5, 7, 11]))

이진탐색

def binary_search(element, some_list):
    start_index = 0
    end_index = len(some_list) - 1
    
    while start_index <= end_index:
        midpoint = (start_index + end_index) // 2
        if some_list[midpoint] == element:
            return midpoint
        elif some_list[midpoint] > element:
            end_index = midpoint - 1
        else:
            start_index = midpoint + 1
    return None

선택정렬

하나씩 값을 확인하여 최소값을 찾고, 0번 인덱스로 옮김
그 다음 작은 값을 1번 인덱스부터 확인하여 찾고 옮기는 작업을 반복

삽입정렬

1이 인덱스 3에 있었다고 가정했을 때, 1을 앞의 숫자들과 비교하면서 제 자리를 찾아갈 때까지 반복

정렬 알고리즘 성능 비교 사이트
https://www.toptal.com/developers/sorting-algorithms

시간복잡도

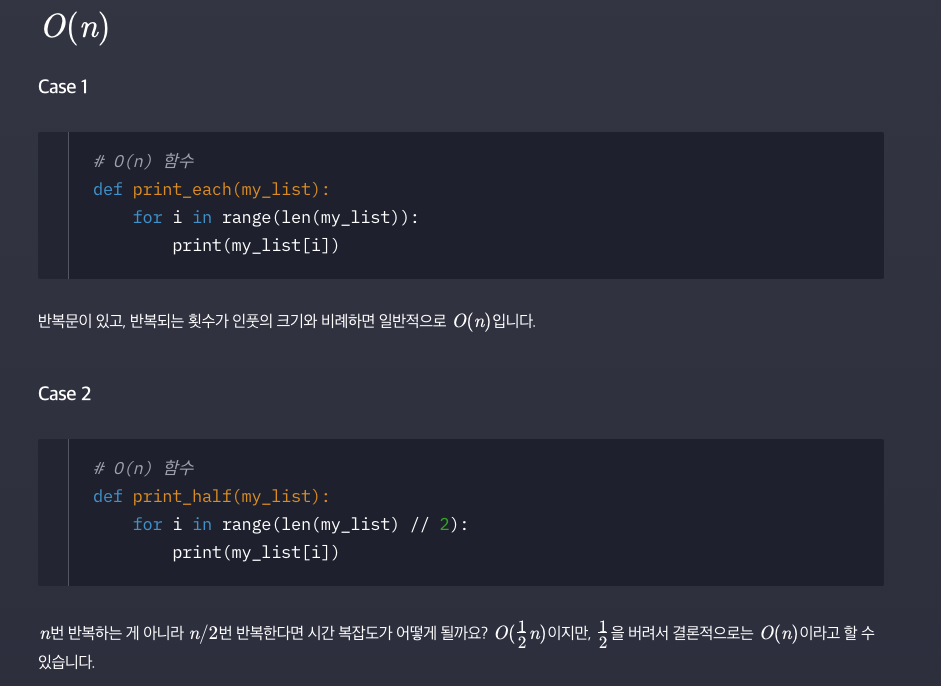
재귀함수

피보나치 수열

# n번째 피보나치 수를 리턴
def fib(n):
    if n < 3:
        return 1
    else:
        return fib(n-1) + fib(n-2)

# 테스트: fib(1)부터 fib(10)까지 출력
for i in range(1, 11):
    print(fib(i))

각 자리수의 합

def sum_digits(n):
    # base case
    if n < 10:
        return n

    # recursive case
    return n % 10 + sum_digits(n // 10)
    
    
# 내가 풀었던 답
def sum_digits(n):
    str_digits = str(n)
    len_digits = len(str_digits)
    if len_digits < 2:
        return n
    else:
        return n//10**(len_digits-1) + sum_digits(int(str_digits[1:]))

리스트 뒤집기

# 파라미터 some_list를 거꾸로 뒤집는 함수
def flip(some_list):
    # base case
    if len(some_list) == 0 or len(some_list) == 1:
        return some_list

    # recursive case
    return some_list[-1:] + flip(some_list[:-1])
    
# 내가 풀었던 답
def flip(some_list):
    if len(some_list) == 1:
        return some_list

    return [some_list.pop()] + flip(some_list)

이진탐색 재귀로 구현

def binary_search(element, some_list, start_index=0, end_index=None):
    # end_index가 따로 주어지지 않은 경우에는 리스트의 마지막 인덱스
    if end_index == None:
        end_index = len(some_list) - 1

    # start_index가 end_index보다 크면 some_list안에 element는 없다
    if start_index > end_index:
        return None
      
    # 범위의 중간 인덱스를 찾는다
    mid = (start_index + end_index) // 2
  
    # 이 인덱스의 값이 찾는 값인지 확인을 해준다
    if some_list[mid] == element:
        return mid

    # 찾는 항목이 중간 값보다 작으면 리스트 왼쪽을 탐색해준다
    if element < some_list[mid]:
        return binary_search(element, some_list, start_index, mid - 1)

    # 찾는 항목이 중간 값보다 크면 리스트 오른쪽을 탐색해준다
    else:
        return binary_search(element, some_list, mid + 1, end_index) 
        
        
# 내가 풀었던 답

def binary_search(element, some_list, start_index=0, end_index=None):
    # end_index가 따로 주어지지 않은 경우에는 리스트의 마지막 인덱스
    if end_index == None:
        end_index = len(some_list) - 1

    mid = (start_index + end_index) // 2
    if element == some_list[mid]:
        return mid
    elif element < some_list[mid]:
        end_index = mid - 1
    else:
        start_index = mid + 1
    
    if start_index <= end_index:
        return binary_search(element, some_list, start_index, end_index)
    else:
        return None

하노이의 탑

def move_disk(disk_num, start_peg, end_peg):
    print("%d번 원판을 %d번 기둥에서 %d번 기둥으로 이동" % (disk_num, start_peg, end_peg))

def hanoi(num_disks, start_peg, end_peg):
    if num_disks == 1:
        return move_disk(num_disks, start_peg, end_peg)
    
    other_peg = (6- start_peg - end_peg)
    
    hanoi(num_disks-1, start_peg, other_peg)
    move_disk(num_disks, start_peg, end_peg)
    hanoi(num_disks-1, other_peg, end_peg)

합병정렬

정렬된 두 개의 배열을 정렬 순서에 맞게 합치는 정렬 방식
전체적인 합병정렬 과정은 Divide and Conquer 방식으로 분할과 정복(정렬)을 반복한다.

def merge(list1, list2):
    i = 0
    j = 0
    
    merged_list = []
    
    while i < len(list1) and j < len(list2):
        if list1[i] < list2[j]:
            merged_list.append(list1[i])
            i += 1
        else:
            merged_list.append(list2[j])
            j += 1
            
    return merged_list + list1[i:] + list2[j:]


# 합병 정렬
def merge_sort(my_list):

    # base case
    if len(my_list) < 2:
        return my_list

    # my_list를 반씩 나눈다(divide)
    left_half = my_list[:len(my_list)//2]    # 왼쪽 반
    right_half = my_list[len(my_list)//2:]   # 오른쪽 반

    # merge_sort 함수를 재귀적으로 호출하여 부분 문제 해결(conquer)하고,
    # merge 함수로 정렬된 두 리스트를 합쳐(combine)준다
    return merge(merge_sort(left_half), merge_sort(right_half))

# 내가 풀었던 답
def merge_sort(my_list):

    start, end = 0, len(my_list)
    mid = (start+end) // 2
    
    list1 = my_list[start:mid]
    list2 = my_list[mid:end]
    
    if len(list1) == 1 or len(list2) == 1:
        return merge(list1,list2)

    return merge(merge_sort(list1), merge_sort(list2))