이번 주에 저희 스터디는 트리(Tree)에 대해서 함께 공부했습니다.
일단 트리라는 것은 계층적인 관계를 나타내는 자료구조입니다. 여기서 트리는 '나무'를 뜻하는 것이 아닌 부모, 자식으로 층층이 이어지는 족보, 또는 기업의 조직도로 계층적으로 표현할 수 있는 것을 말합니다.
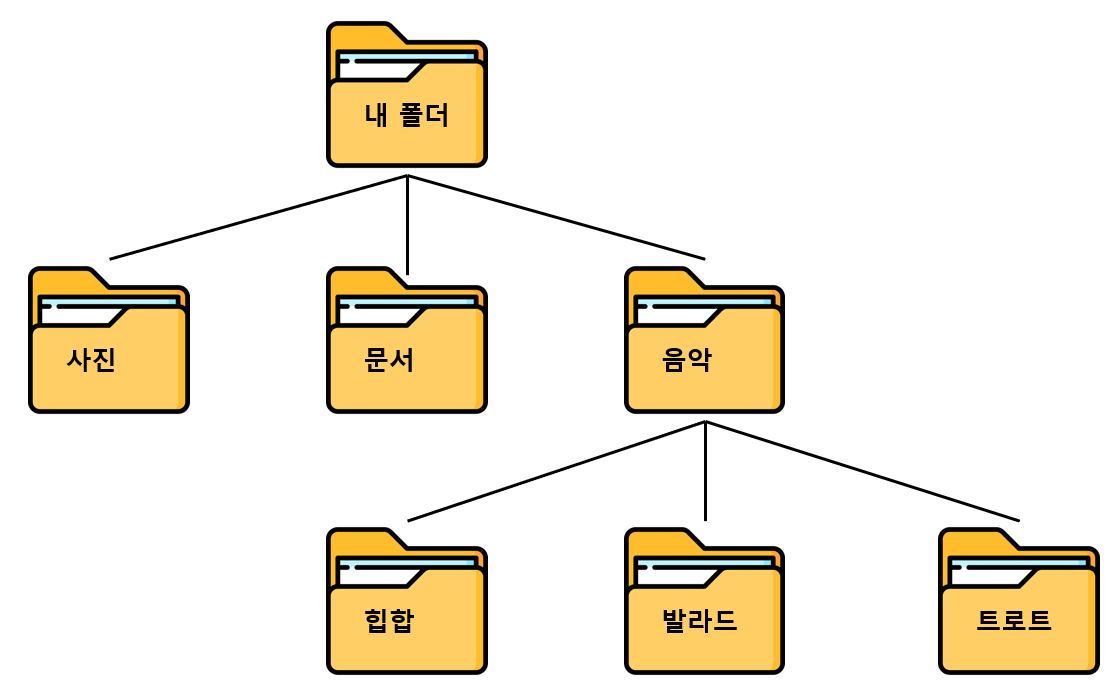
아래의 이미지는 폴더, 하위 폴더, 다시 하위의 하위 폴더로 이어지는 컴퓨터 디렉터리 계층 구조를 나타냅니다.
위 이미지에서 내 폴더, 사진, 문서, ..., 등 폴더를 노드(Node)라고 하고, 음악 하위 폴더인 힙합, 발라드, 트로트 폴더를 자식 노드(Child Node)라고 합니다. 반면에 음악은 힙합, 발라드, 트로트의 부모 노드(Parent Node)라고 하며, 같은 부모 아래에서 자식 노드 서로를 형제 노드(Sibling Node)라고 합니다. 또한 자식이 없는 노드(사진, 문서, 힙합, 발라드, 트로트)들은 리프 노드(Leaf Node)라고 합니다.
이 트리의 형태에 따라 종류가 다양합니다.
여기서 부모 노드가 자식 노드를 최대 2개씩만 갖고있는 트리를 이진 트리(Binary Tree)라고 합니다.
이 이진 트리의 특징은 부모 노드의 왼쪽 자식은 부모 노드의 값보다 작아야 하며, 오른쪽 자식은 부모 노드의 값보다 큰 값이 저장되어 있다는 것입니다.
또한, 왼쪽 자식부터 채워지며, 마지막 계층을 제외한 모든 자식 노드가 채워진 트리를 완전 이진 트리(Complete Binary Tree)라고 합니다.
하나의 자식 노드를 가진 트리가 하나도 존재하지 않을 경우에 정 이진 트리(Full Binary Tree)라고 합니다. 노드들의 자식이 하나도 없거나 두 개의 자식으로만 구성될 경우를 의미합니다.
이 트리의 형태에 따른 개념을 생각했을 때, 알 수 있는 것은 어떤 트리가 정 이진 트리면 이는 완전 이진 트리일 수 있지만 완전 이진 트리라고 반드시 정 이진 트리일 수는 없습니다.
그리고 모든 레벨의 노드가 가득 차있는 트리로 포화 이진 트리(Perfect Binary Tree)라고 합니다.
이 트리에서 중요한 것은 순회(Traversal)입니다.
이 순회는 트리 내부를 이리저리 돌아다닐 수 있는 작업입니다. 이러한 트리의 순회는 전위 순회, 중위 순회, 후위 순회로 나뉩니다.
각 순회에 대해서 간단히 설명하자면, 전위 순회는 루트 노드에 대한 작업이 가장 먼저 일어나고, 왼쪽, 오른쪽 자식 순으로 탐색합니다.
중위 순회는 왼쪽 자식 노드를 탐색하고, 루트 노드를 탐색하고, 오른쪽 자식 노드를 탐색하는 방식입니다.
후위 순회는 왼쪽 자식 노드를 탐색하고, 오른쪽 자식 노드를 탐색하고, 루트 노드를 탐색하는 방식입니다.
이러한 순회의 기본적인 구현 형태는 재귀적입니다.
트리의 개념을 공부하고 릿코드에서 트리 구현 문제를 풀기 시도를 해봤습니다만 쉽지 않았습니다. 강의를 들으면서 이해는 갔지만 막상 문제로 접하니 쉽게 해결할 수 없었습니다.
트리의 속성을 이용하여 재귀적으로 호출하는 것까지는 알겠지만 문제에서 어떤 특정 노드를 삭제했을 때, 삭제된 특정 노드의 자리를 채워줘야 하는 과정이 강의를 들었음에도 쉽게 생각나질 않았습니다. 노드를 삭제했을 때, 여러 가지 경우가 있을 수 있기 때문에 아직 저한테는 복잡하다고 느꼈습니다.
막상 그룹원 분들의 해결 과정을 듣고보니 생각보다 간단했습니다. 특정 노드를 삭제했을 때, 그 이후 처리 방법은 여러 가지 해결 방법이 있지만 그 중에서 제일 이해하기 쉬운 것이 삭제된 노드의 오른쪽 서브 트리에서 가장 최솟값을 찾아 탐색하고 그 값을 삭제된 노드 자리로 대체하면 된다는 것이였습니다. 물론 그 이후에 옮겨진 최솟값 자리 또한 처리해야 합니다.
점점 강의의 내용이 더 어려워 지고 있기 때문에, 개념이라도 확실히 이해할 수 있도록 하겠다고 느꼈습니다. 아직 저는 훨씬 더 발전할 필요가 있는 것 같습니다.