저희 스터디는 이번 주에 힙(Heap)에 대해서 공부했습니다.
힙(Heap)
일단 힙이라는 것은 트리 모양이 쌓아놓은 무더기와 흡사하다는 점에서 힙이라고 부릅니다.
여기서 2가지 조건을 만족해야 힙이라고 볼 수 있습니다.
-
항상 완전 이진 트리의 모습이어야 합니다.
-
비어있는 트리 또는 루트 노드의 값이 왼쪽, 오른쪽 자식의 값보다 크거나 같아야 합니다. 여기서 왼쪽과 오른쪽 자식 사이에는 어느 쪽 값이 크든지 상관 없습니다. 단, 왼쪽과 오른쪽 노드를 루트로 하는 하위트리는 힙이어야 합니다.
최대 힙(Max Heap) & 최소 힙(Min Heap)
쌓아놓은 더미에서의 정상을 루트 노드라고 했을 때, 그 루트 노드의 값이 가장 크면, 가장 우선순위가 높다고 할 수 있습니다. 그것을 최대 힙(Max Heap)이라고 부릅니다. 최대가 존재하면 당연히 최소도 존재합니다. 최대 힙과는 반대로 루트 노드의 값이 가장 작으면 우선순위가 더 높다는 의미로 최소 힙(Min Heap)입니다.
힙의 가장 큰 특징은 완전 이진 트리의 모습이라고 불 수 있습니다.
완전 이진 트리는 배열로 표시하는 것이 효율적이기 때문에 힙은 항상 배열로 구현됩니다. 그래서 힙에 대한 강의를 들을 때, 설명의 편의상 트리를 그리며, 힙의 구현은 배열로 합니다.
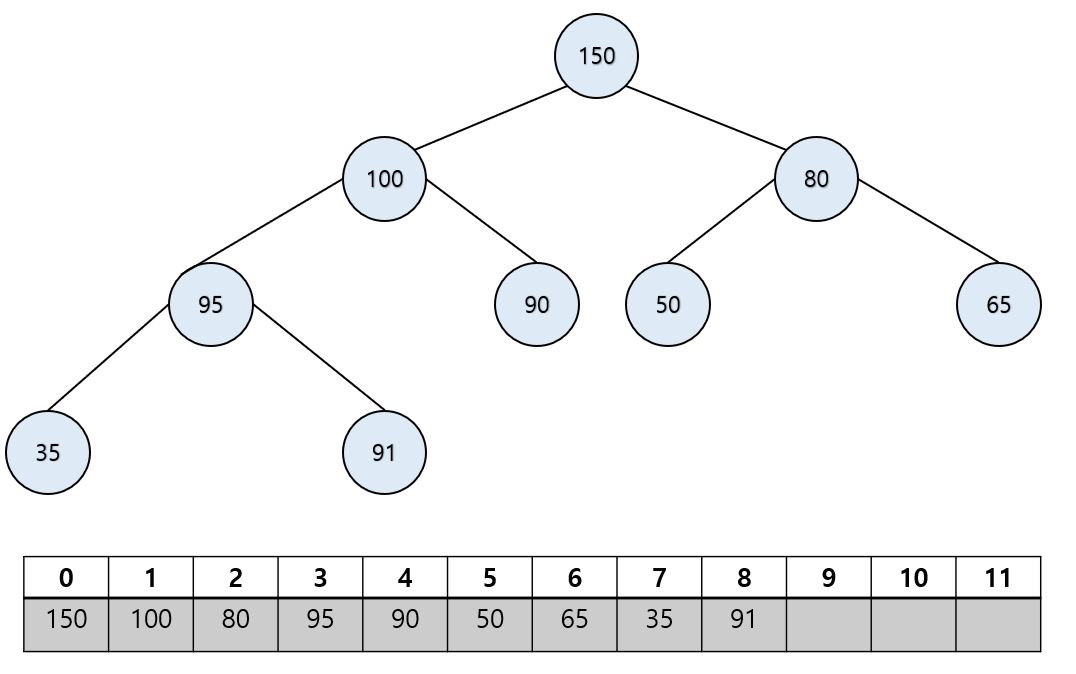
아래의 이미지는 완전 이진 트리와 배열로 최대 힙을 나타냈습니다.
여기서 중요한 점은 트리의 부모 자식 관계는 인덱스 연산으로 가능합니다.
-
인덱스 K에 있는 노드의 왼쪽 자식은
2K + 1에 오른쪽 자식은2K + 2에 있습니다. -
인덱스 K에 있는 노드의 부모 노드는
(K-1) / 2에 있습니다.
예를 들어, 위에서 값이 95인 노드는 인덱스 3에 존재하는데, 이 노드의 왼쪽 자식인 값 35는 인덱스 2 * 3 + 1 = 7
에 존재하고 이 노드의 부모 노드인 100은 인덱스 (3-1) / 2 = 1에 존재한다는 것을 알 수 있습니다.
이 힙은 최대 / 최소를 기준으로 데이터를 찾는 연산은 빠르게 동작할 수 있기 때문에 O(1)의 시간복잡도가 소요됩니다.
또한 삽입과 삭제는 O(log N)의 시간복잡도가 소요됩니다.
자바에서는 데이터가 들어온 순서에 상관없이 우선 순위가 높은 데이터를 먼저 처리해주는 힙 구조인 Priority Queue(우선순위 큐) 클래스가 제공됩니다.
기본적으로 오름차순으로 정렬되며, Collections.reverseOrder()을 통해 내림차순으로 정렬할 수 있습니다. 또한 정렬 기준을 바꾸고 싶다면 람다식 또는 Comparabtor, Comparable을 이용하면 됩니다.
알고리즘 문제로 힙에 대해서 풀어봤는데, 자바에서 우선순위 큐가 제공되기 때문에 몇 개는 쉽게 풀었습니다. 하지만 작업 스케줄러에 대한 알고리즘 문제를 릿코드에서 풀었는데, 이걸 어떻게 우선순위 큐를 이용하여 풀 수 있을까 고민하다가 결국 풀지 못했습니다. 그래서 이 문제를 푸신 다른 분들의 설명을 들었는데, 저는 쉽게 생각을 못했을 것 같다는 느낌을 받았습니다. 그냥 어떻게든 Priority Queue로만 사용해서 해결해야겠다는 생각만 해서 다른 부분을 생각하지 못했던 것 같습니다. 문제를 해결하기 위해 바라보는 관점을 다각화해서 접근하는 능력을 길러야겠다고 느꼈습니다.