[AIFFEL] 22.Feb.07 - Understanding_of_Layers:Linear, Convolution

오늘의 학습 리스트

• 딥러닝은 y = Wx + b에서 최적의 W(Weight)과 b를 찾는 과정!

• 이 때 신경망의 종류(?)마다 다른 Weight의 특성을 갖고 있고, 그래서 올바른 Weight을 정의하는 과정이 중요하다.

• 딥러닝을 이해하는 좋은 방법 중 하나는 데이터의 변화를 좇는 것이다.

• 신경망의 Weight이라 표현하지만, 사실 layer마다의 weight이다.

Linear layer

• Fully Connected Layer, Feedforward Neural Network, Multilayer Perceptrons, Dense Layer... 다 선형레이어를 치징하는 말임

• linear 레이어는 선형변환을 통해 데이터를 특정 차원으로 옮긴다.

  • 이 때 차원이 더 많아지면 데이터가 더 풍부하게 되는 것이고,
  • 차원이 줄어들면 데이터가 집약시키는 것이다.

• 참고로 python code에서 레이어를 생성하고 call하면서 무언가 input을 넣었다면, 해당 레이어에 다시 인풋을 넣으려니까 뭔가 오류가 생긴다.(한번 쓴 레이어는 또 쓰는 건 아닌가 보다)

• tensorflow에서는 선형변환 후 차원을 유지한다.

  • 이러면 Dense(units=1)에 input으로 넣어도 (64, 4, 1) 같이 끝 부분만 1로 줄어들게 되는데
  • 방지하려면 tf.squeeze(axis=-1) >>> (64, 4)를해서 불필요한 차원을 줄여준다.
    • 참고로 제대로 된 tensor를 squeeze하려 하면 그냥 그대로 유지된다.(tf.squeeze( (64, 4,)행렬 ) >>> (64, 4)행렬)
  • 실험으로 Flatten()은 그럼 전체를 다 펴주나 해봤는데,
  • Flatten()은 차원을 유지하진 않지만, 전체 다 펴주지는 않는다.
  • 대신 (64, 4, 2)를 Flatten()에 넣으면 (64, 8)로 바꿔준다.
  • 즉 차원을 1개 줄이면서 펴준다.
  • 아 근데 이건 3차원 -> 2차원에만 해당되고, 2차원에서는 Flatten()을 해도 1차원으로 되지 않는다...((64,8) -> (64, 8)로 계속 나옴)

• tf.keras.Layers.layer.count_params()

  • 해당 레이어의 파라미터 수를 반환해준다.

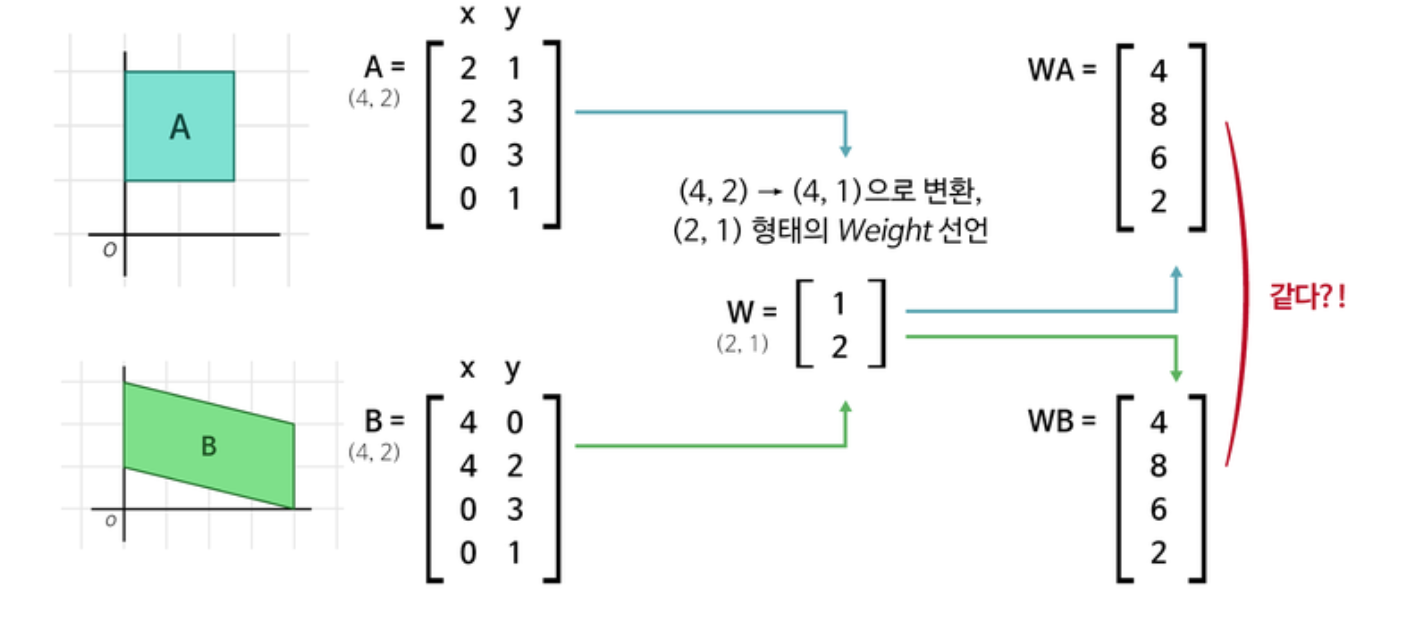
• 선형변환에서...

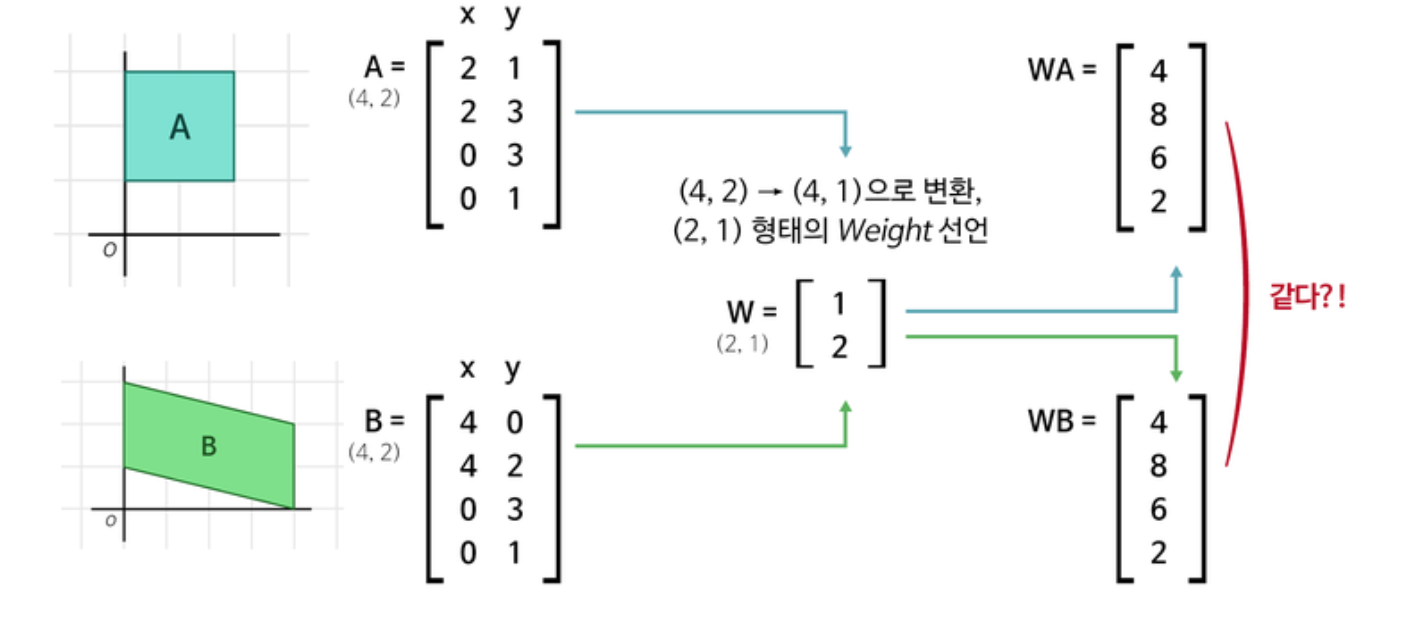  출처 : 아이펠

  • 데이터 차원을 줄이려했는데 다른 데이터가 같아짐.
  • 이러면 안돼서 데이터 차원을 늘렸다가 줄일 예정

• 데이터 차원을 늘리는 선형변환 후 줄여감

  • 이러면 중간에 서로 간 다른 특징들(데이터 값)이 생성된다.
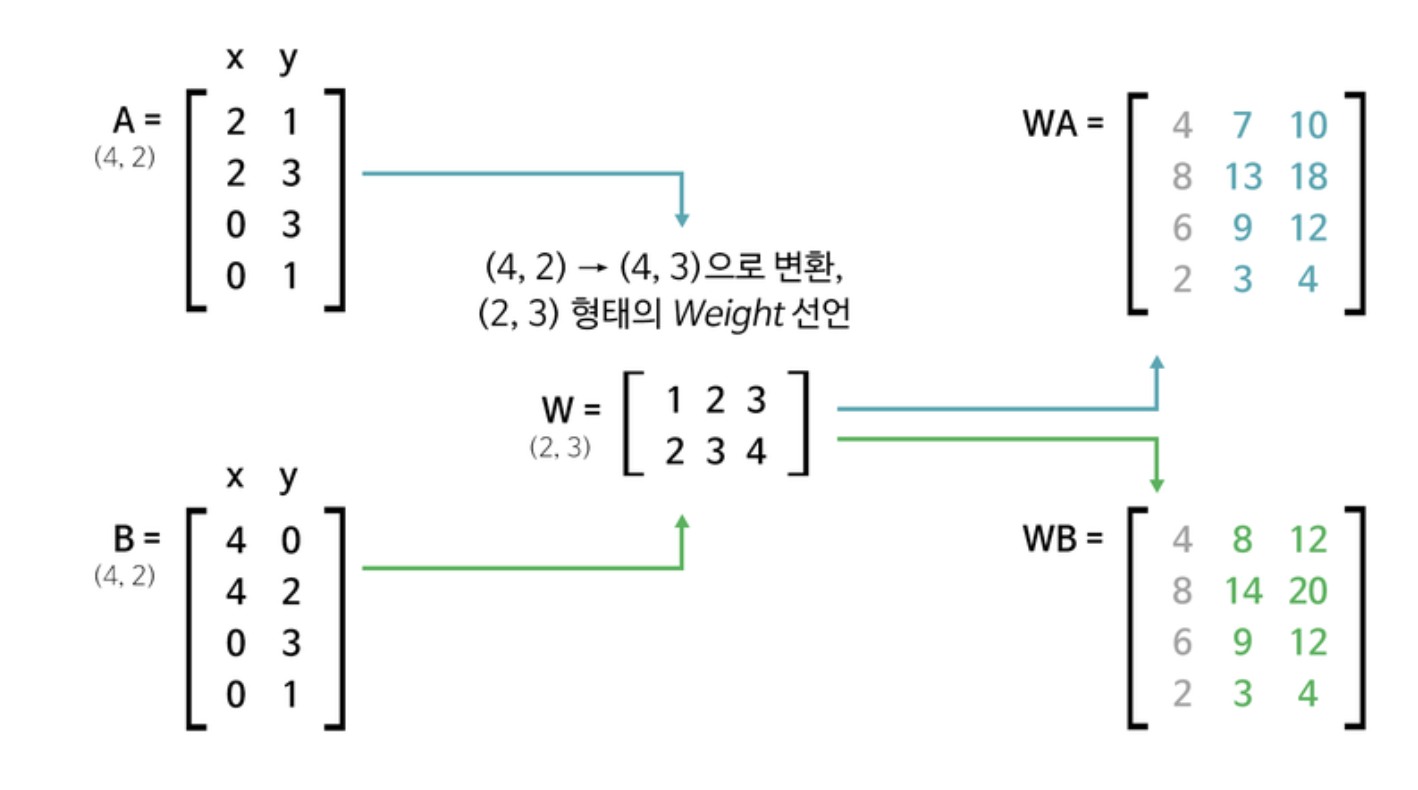    출처 : 아이펠

• bias(편향)

  • 데이터를 선형변환 했을 때 아무리 해도 목표 데이터 모양으로 바꾸기 힘들 때가 있음
  • 그럴 때 단순한 평행이동을 통해 맞추는 것
  • $Wx$에 단순히 더하는 것이기 때문에 shape은 (선형변환 후 결과의 차원, )이 된다.

Convolution

• 단순히 선형변환의 결과로서 나오는 값들이 1줄짜리 벡터나 1개의 스칼라 값으로 표현될 텐데, 이미지 데이터의 경우 spatial 정보가 없어져서 해석하기 어려워진다.
• 이를 위치마다의 합성곱을 통해 해결함.
• 사진 필터 기능들이 이런 convolution을 통해 해결된단다.
• (https://aishack.in/tutorials/image-convolution-examples/)
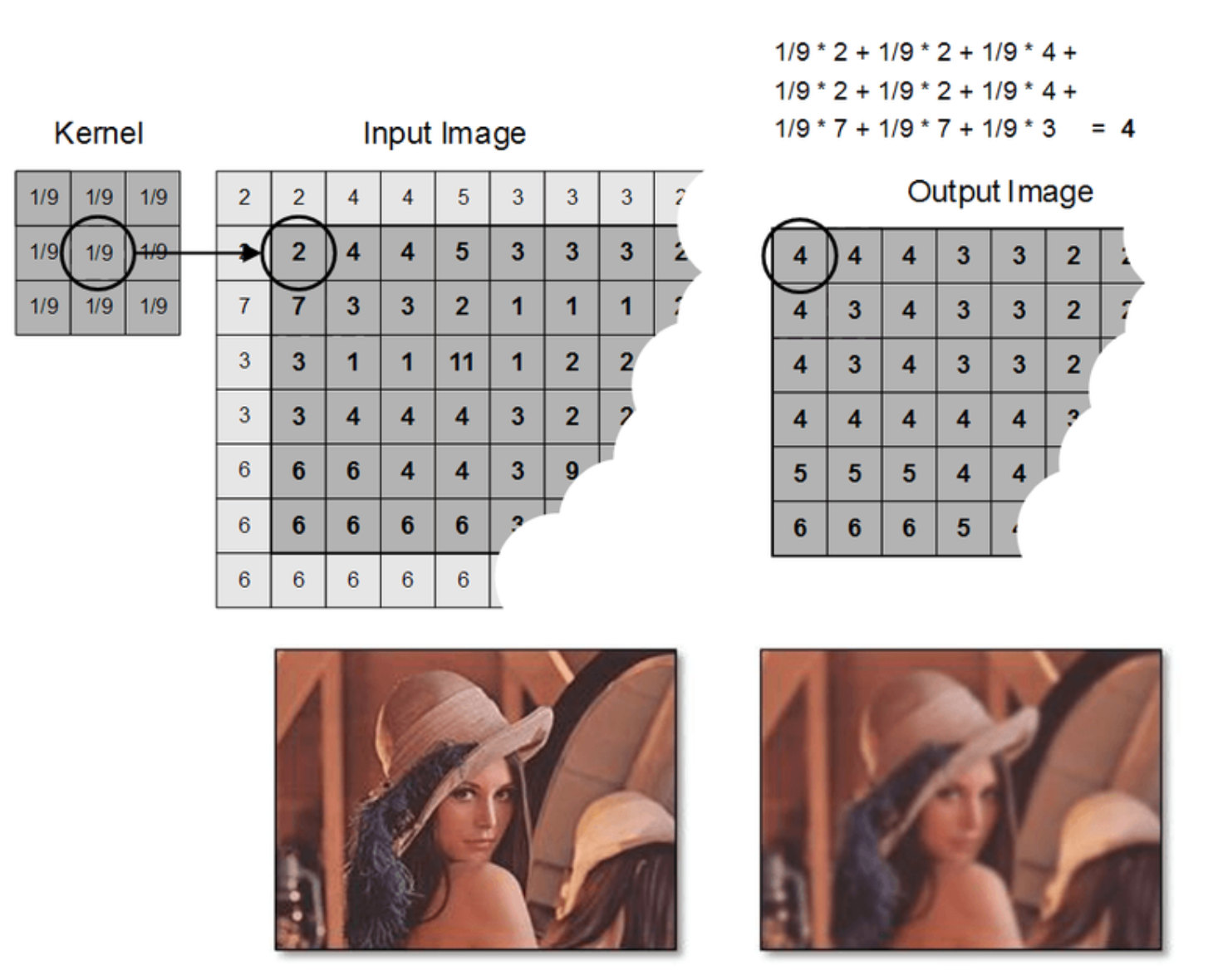  - 출처 : 아이펠
  • blur 필터의 예제
• Padding의 목적
  • 이미지 크기 유지
  • 코너 부분 정보 손실 방지
    • 이 부분 잘 와닿지 않았었는데, 생각해보면,
    • 패딩을 함으로써 코너 부분 픽셀의 연산이 한 번 더 추가되는 것이다.
    • 그래서 그 값의 정보를 보존하게 되는 것
• 필터의 사이즈는 대부분 1x1, 3x3, 5x5 같이 홀수인 이유
  • Convolution에서 중앙 픽셀의 정보를 갖는 것이 위치를 정의하기 쉽게 해주기 때문
• 필터라는 단어의 의미
  • 사실 잘 몰랐는데, 이 3x3 필터 같은 게 필터라고 불리는 이유가 있는 것 같다.
  • 즉, 한 이미지를 어떤 특정 값의 필터로 거치면 blur가 되고,
  • 어떤 특정 값의 필터로 거치면 모서리를 찾아주고 등등...
  • 이러다 보니 나중에 이것들이 겹치고 등등 하면,
  • 이미지 내에 어떤 물체를 찾아주는 필터역할을 할 수 있는 것이다.
• 파라미터 갯수는
  • 필터 개수 * (가로 크기 * 세로 크기 * 깊이 + 1)
• Convolution 레이어는 입력의 정보를 잘 집약시키기 때문에 여러 겹을 중첩하는 것이 일반적이고, 중첩할수록 최종 Linear 레이어는 작아지게 된다.(파라미터도 줄어든다)
• Linear <-> Convolution은 약간 서로 반대되는 특성이 있는데,
  • Linear : 모든 입력과 모든 출력이 연결된다. 즉, 가중치를 통해 입력 데이터 전체와 출력 데이터 전체가 영향을 주고 받는데
  • Convolution : 반면 local 정보 보존에만 집중한다.
  • 즉 Linear는 local 정보가 소실되는 반면, 전체 데이터의 정보들은 보존된다.
  • 즉, Convolution은 중요한 local 정보만 핵심적으로 추린 것!
• CNN 중간 gradient, activation map의 visualisation(cs231n lecture 5 자료)
  • https://cs.stanford.edu/people/karpathy/convnetjs/demo/cifar10.html

MaxPooling

• 증가되는 파라미터 수는 없다.
• downsampling을 통해 pooling 후 convolution을 하면 이전과 같은 필터 사이즈여도 기존 인풋 이미지 내 더 큰 영역을 파악하게 되는데 이를 receptive field가 커진다고 표현한다.
• 어찌보면 3/4를 날리는 셈인데, 왜 쓰는가?(장점이 무언가?)
  • 사람들 각자의 의견이지만,
  • translational invariance 효과
    • 이미지가 약간 shift하는 듯이 되는데, 이 때 두드러진 특징을 뽑아내는 MaxPooling은 동일한 특징을 안정적으로 잡아낸단다.
  • Non-linear 함수와 동일한 feature 추출 효과
    • ReLU 같은 것도 앞단 레이어의 정보를 날려버림...
    • 그러나 특징을 잘 추출해낸다는 장점이 있는데 그게 생김
  • Receptive Field 극대화 효과
    • 단순히 Conv만 쓰면 연산량 증가, 파라미터 수 증가 등 되는데
    • Pooling하면 그런 것 없이 Receptive field가 커짐

Deconvolution

• convolution하면 그래도 정보 손실 아닐까...?

• 이것을 인코더(Conv->MaxPooling....Conv->MaxPooling), 디코더(Conv -> UpSampling -> Conv -> UpSampling)해서 동일한 사이즈로 회복시켰을 때 어떤지 확인해볼 수 있다.

• UpSampling의 방법은 크게 3가지가 있다.

  • Nearest Neighbor : 복원해야 할 값을 가까운 값으로 복제
  • Bed of Nails : 복원해야 할 값을 0으로 처리
  • Max Unpooling : Max Pooling 때 위치를 기억했다가 나중에 거기에다가 gradient를 복원시킴
    • 잘 안쓰인단다..
    • 여튼 이 링크가 좋은듯(https://www.oreilly.com/library/view/hands-on-convolutional-neural/9781789130331/6476c4d5-19f2-455f-8590-c6f99504b7a5.xhtml)
  • 시각적인 도움(https://analysisbugs.tistory.com/104)

• 수학적 역연산이 실행되는 제대로된 deconvolution을 하려면

  • Transposed convolution을 해야 한다.

Deep ML

• Flatten()은 공간 구조를 없애버림.
• 그래서 공간 구조를 가진 채 vector화 하기 위해서 아래와 같은 방법도 있음
  • Flatten대신 그 자리에 1x1 convolution로 하고, depth를 N으로 함. 이걸 Fully Convolutional layer라고도 한단다.
  • 그래서 (가로 세로) depth(N)이 된 걸 Global Average Pooling한단다.
  • 그럼 가로 * 세로 픽셀 하나마다 N개의 평균 값을 구해서 vector화해준다.
    • 여기서 N개의 activation map은 서로 다른 특징이라고 보면 되겠다.
  • 그러면 가로, 세로가 무분별하게 flatten되는 게 아니라 나름 공간 구조를 가진채 vector화 된다.
• Translation invariance
  • 이미지의 경우 이미지 내 특정 물체의 위치가 바뀌어도 그것에 대한 output, 즉 은닉층 내의 output 혹은 최종 예측값은 변하지 않는 것(맞나...?)
  • 이는 Maxpooling을 통해 살짝 이루어지고
    • 여기서 downsampling만 하는 게 아니라, 2x2내에서의 살짝인 shift는 output에 변하는 영향을 주지 않는다.
  • CNN의 특징(커널 사이즈 내에서도 동일하게 invariance할 수 있음)
  • softmax의 특징(잘 모르겠음)
  • 덕분에 CNN의 값은 translfation invariance를 유지할 수 있다.
  • 링크(https://ganghee-lee.tistory.com/43)