[AIFFEL] 22.Feb.16 - Likelihood_MLE_MAP

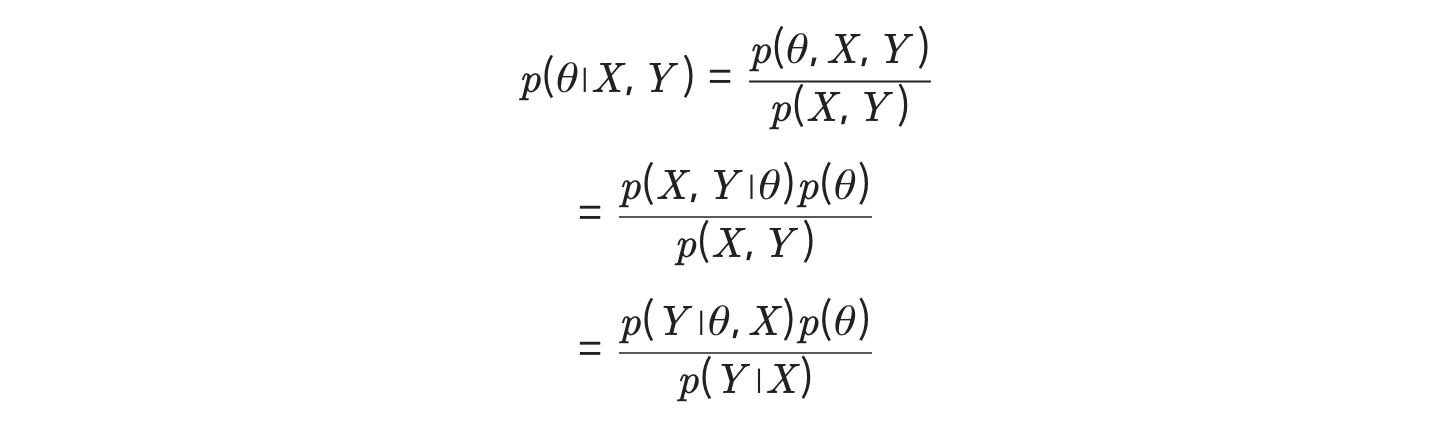
오늘의 학습 리스트

• 서론에서 머신러닝의 목적을 말하는데 와닿는다.

"우리에게는 데이터의 집합이 있고, 데이터가 따르는 확률 분포를 알고 싶어 합니다.

데이터의 분포를 안다면 새로운 입력 값이 들어와도 적절한 출력값을 추정할 수 있을 테니까요.

하지만 데이터셋의 크기는 유한하기 때문에 데이터가 따르는 정확한 확률 분포를 구하는 것은 불가능합니다. 그래서 파라미터(parameter, 매개 변수)에 의해 결정되는 머신러닝 모델을 만든 다음, 파라미터의 값을 조절함으로써 데이터의 분포를 간접적으로 표현합니다.

모델이 표현하는 확률 분포를 데이터의 실제 분포에 가깝게 만드는 최적의 파라미터 값을 찾는 것이 머신러닝의 목표라고 할 수 있습니다." 출처:아이펠

• 베이즈 정리(Bayes' Theorum)
  • 이거 계속 나오는데 이것도 제대로 정리하고 넘어가자...!
  • 일단 직관적인 의미를 보면 전체에서의 확률, 그리고 조건이 주어졌을 때의 확률... 뭐 이런 식으로 생각해보려는 이론인 것 같다.(meek Steve의 librarian vs farmer case...)
• likelihood
  • 베이즈 정리랑 연관되지 않은 것일 수도 있지만,
  • pdf가 있을 때 그 함수의 y값으로 나오는 게 likelihood
  • 즉 pdf를 통해서 적분을 하면 어떤 구간의 확률(면적)을 구할 수 있었는데
  • 면적말고 y값을 이용하는 것
  • 나의 직관적 의미로는 확률이란 말보다, 얼마나 많은 후보(가능성)이 나오는지...?
• MLE(Maximum Likelihood Estimation)
  • 그래서 위의 likelihood를 이용하는 건데
  • 직관적인 의미로는
  • 데이터가 있을 때 그걸 조건으로 했을 때 알고자 하는 확률은 구하기 힘드니
  • 우리가 알고자 하는 것이 있을 때 데이터가 나왔던 확률을 알아보자
  • 그게 likelihood이고
  • 이것의 maximum 값을 찾는 것이
  • 만약 그게 파라미터 공간 안에 있었다면
  • 로스 값의 최저점(?)이 되는 것이어서 그것을 찾음을 통해
  • 방정식의 해를 구하는 방식인 것 같다.(맞나...?)
• MAP
  • 이게 베이즈 정리를 이용하는 건데
  • 위처럼 likelihood는 알고 있으니
  • 혹시 전체 그림에서 우리가 알고자 하는 게 나오는 확률은 얼마나 되나..를 구하고
  • 그것과 likelihood를 곱하면(베이즈정리)
  • 데이터가 있을 때 그것을 조건으로 하는 우리가 알고자 하는 어떤 것의 확률을 구할 수 있다는 것

  • 근데 결론은 MLE, MAP 둘다 아직 애매하게 이해하는 상황이어서 LMS노드와 다른 유튜브 강의를 통해 더 정확하게 이해해야 할 것 같다....

• annotation하는 방법...
  • 좌표값을 주는데 그것을 저렇게 리스트 요소로 만들어놓으면 편하구나..

fig, ax = plt.subplots()
ax.scatter(input_data, label)
ax.plot(model_x, model_y)

for i, text in enumerate(likelihood):
    ax.annotate('%.3e'%text, (input_data[i], label[i]))

• 드디어 $\Pi$의 의미를 알았다......... a set of elements 모두를 곱하라는 것....

• np.append()라는 함수가 있다.
  • axis= 파라미터로 축을 지정할 수 있는데
  • 약간 stack 같은 느낌이다.
• keras.Model()은 인풋과 아웃풋만 넣어주면 그걸 통과하는(?) 모델을 만들어준다.
  • 근데 아무 인풋이나 아웃풋은 아니고
  • 이미 해당 모델을 지나해서 나온 인풋과 아웃풋을 넣어주면 그렇게 작동하는 것 같다.

Deep ML

• 가중치 시각화
  • 가중치(filter)행렬을 시각화해서 밝게 나오면 그곳의 가중치 값은 높다는 것이다.
  • 훈련 후에 이렇게 나오는 가중치 값은 뭔가 그 필터에서 활성화해서 보고싶은 부분(필터 입장에서)이라고 생각하면 될 것 같다.
• 특성맵 시각화
  • 그리고 결과로 나온 특성맵도 시각화할 수 있다.
  • 특성맵을 시각화한다는 것은 필터에 거쳐서 합성곱을 한 결과가 어느 부분에서 높은 값, 즉 활성화, 즉 밝게(?) 보이는지를 확인할 수 있는 것이다.
  • 그러나 그것도 입력층에 가까운 일부 층의 특성맵만 볼 수 있는 것이고, 더 깊어질수록 해석하기 난해해진다.