DP의 목적
메모리를 사용해서 중복 연산을 줄이고, 중복 연산을 줄여서 수행 속도를 개선한다.
동적 프로그래밍(DP) 의 핵심 개념
-
부분 문제의 중복: 큰 문제를 작은 부분 문제로 나눌 수 있으며, 이러한 부분 문제가 여러 번 반복될 때 동적 프로그래밍이 유용.
-
최적 부분 구조: 문제의 최적 해결 방법이 부분 문제의 최적 해결 방법으로 구성될 수 있음.
-
메모이제이션 (Memoization): 재귀적 접근에서 이미 계산된 결과를 저장하여 중복 계산을 피하는 방법.
-
타뷸레이션 (Tabulation): 바텀업 접근 방식으로, 작은 문제부터 해결해 나가면서 결과를 테이블에 저장하는 방법.
만약, f(5) 의 피보나치 수열을 재귀 방식으로 구하려면 아래와 같은 연산이 수행 되어야 한다.
public class fibonacci {
public static int fibonacci(int n) {
if (n <= 1)
return n;
else
return fibonacci(n - 2) + fibonacci(n - 1);
}
public static void main(String[] args) {
System.out.println(fibonacci(10));
}
}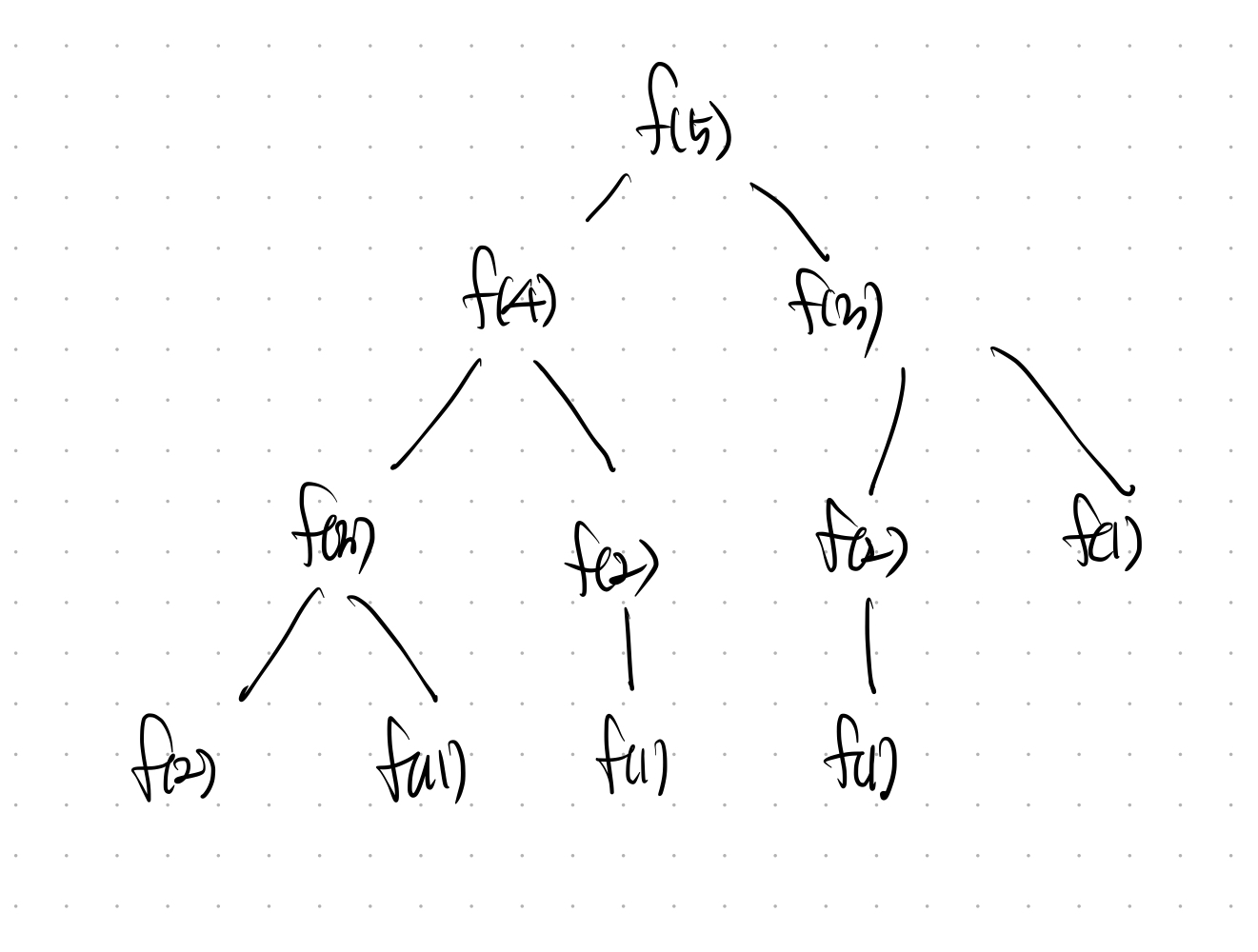
그림에서 볼 수 있듯이 여러번 수행되는 연산들이 존재한다. 수가 적은 경우엔 어느정도 재귀의 방법으로 모든 연산을 수행할 수 있겠으나, 수가 높아질수록 수행 속도는 기하 급수적으로 많아지기에 재귀적 방법은 그닥 효율적이지 못하다.
DP 는 이러한 문제를 해결하기 위해 이전의 결과 값을 따로 저장하여, 동일한 연산이 필요한 값이 있을 때 저장된 값에서 불러와 사용한다.
DP를 활용한 예시 코드
- 탑다운 접근 방식 (Top-Down Approach)
public class dpFibonacci {
static long[] memo;
public static long fibonacci(int n) {
if (n <= 1)
return n;
else if (memo[n] != 0)
return memo[n];
else
return memo[n] = fibonacci(n - 1) + fibonacci(n - 2);
}
public static void main(String[] args) {
memo = new long[101];
System.out.println(fibonacci(100));
}
}
재귀 방식과 다른 점은 f(N) 의 값이 memo 배열에 연산 결과가 존재하는지 확인하고, 존재한다면 그 값을 이용한다. 또한 결과를 memo 배열에 저장한다.
이를 메모이제이션(Memoization) 이라고 하며 제일 큰 문제부터 내려가는 탑다운 접근 방식 (Top-Down Approach) 이다.
바텀 업 방식
public class dpFibonacci {
public static long fibonacci(int n) {
if (n <= 1) {
return n;
}
long[] dp = new long[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
public static void main(String[] args) {
System.out.println(fibonacci(100));
}
}바텀업 방식은 아래서 부터 올라간다. 반복문에서 볼 수 있듯이 피보나치 N 까지의 값을 구하기 위해 처음부터 진행한다. 연산을 수행하며 결과를 dp 배열 에 담으며 연산과 메모리를 줄인다.

