dfs에 관하여
dfs란 deapth-fisrt-search의 약자로 깊이 우선 탐색을 의미한다.
깊이 우선 탐색의 동작 방식
깊이 우선 탐색은 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 모두 탐색하는 방식이다.
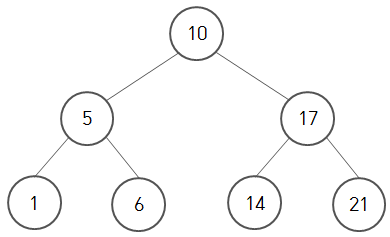
깊이 우선 탐색을 왼쪽 부터 진행한다고 가정하면 위의 트리에서는
10 -> 5 -> 1 -> 6 -> 17 -> 14 -> 21 순으로 탐색이 이루어진다.
이러한 탐색 방식의 특징은 다음과 같다.
1. 모든 노드를 방문 할 수 있다.
2. 다만 검색 속도는 bfs에 비해 느리다
깊이 우선 탐색은 스택 또는 재귀함수를 통해 구현 가능하다.
-재귀함수란 함수가 자기 자신을 호출하는 프로그래밍 기법이다.
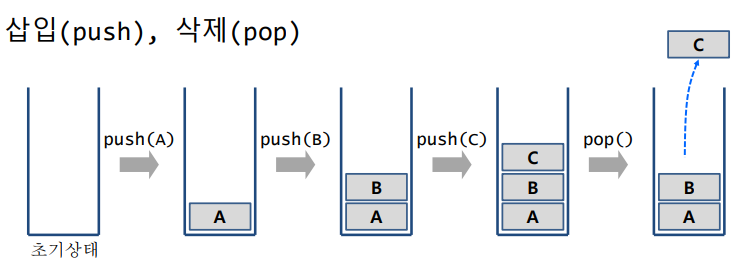
-스택이란 쌓아놓은 더미를 뜻하는 자료구조로 후입 선출의 방식을 띈다.
아래는 파이썬을 통해 구현한 깊이 우선 탐색의 코드이다.
Graph = {'a':['b'],
'b':['a','c','h'],
'c':['b','d'],
'd':['c','e','g'],
'e':['d','f'],
'f':['e'],
'g':['d'],
'h':['b','i','j','m'],
'i':['h'],
'j':['h','k'],
'k':['j','l'],
'l':['k'],
'm':['h']
}
def dfs(graph, start_node):
visited = [] #방문한 노드를 담을 리스트
stack = [] #방문 예정인 노드를 담을 배열
stack.append(start_node) #시작 노드 담기
while stack: #모든 노드를 방문 할 때까지 반복
node = stack.pop() #후입 선출인 스택 구조로 뒤에 녀석을 뽑아냄
if node not in visited: #이미 방문한 노드 x
visited.append(node) #방문 리스트에 담기
stack.extend(graph[node]) #스택에 해당 노드의 자식 노드들 추가
print(visited)
dfs(Graph, 'g')아래는 재귀를 통해 구현한 깊이 우선 탐색의 코드이다.
def dfs(graph, start_node):
visited[start_node] = True
for i in graph[start_node]:
if not visited[i]:
dfs(graph,i)
bfs에 관하여
bfs란 breadth-fisrt-search의 약자로 너비 우선 탐색을 의미한다.
너비 우선 탐색의 동작 방식
너비 우선 탐색은 노드에서 시작하여 인접한 노드를 먼저 탐색하는 방식이다.

너비 우선 탐색을 왼쪽 부터 진행한다고 가정하면 위의 트리에서는
10 -> 5 -> 17 -> 1 -> 6 -> 14 -> 21 순으로 탐색이 이루어진다.
이러한 탐색 방식의 특징은 다음과 같다.
1. 최단경로를 찾기 적합하다.
2. 다만 메모리를 많이 소비한다.
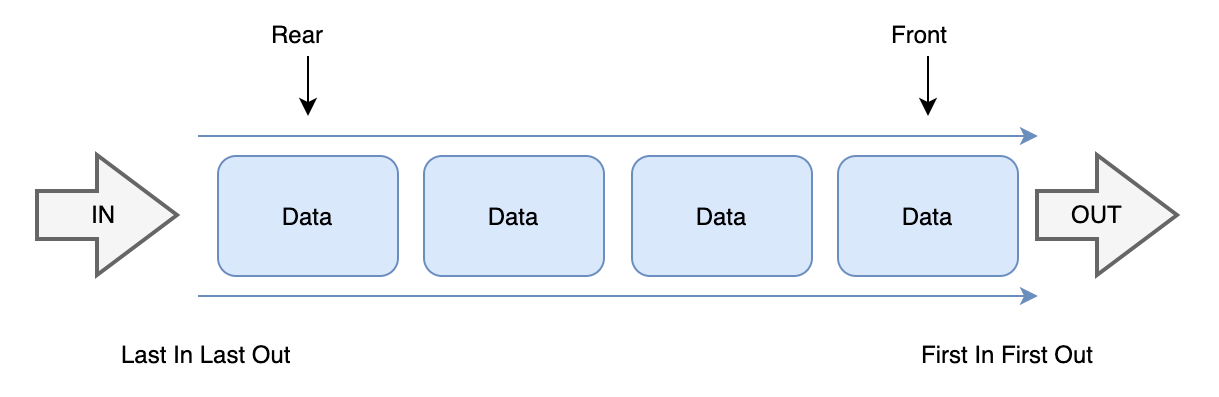
너비 우선 탐색은 큐를 이용해 작동한다.
-큐는 선입 선출의 방식을 사용하는 자료구조이다.
아래는 파이썬을 통해 구현한 너비 우선 탐색의 코드이다.
Graph = {'a':['b'],
'b':['a','c','h'],
'c':['b','d'],
'd':['c','e','g'],
'e':['d','f'],
'f':['e'],
'g':['d'],
'h':['b','i','j','m'],
'i':['h'],
'j':['h','k'],
'k':['j','l'],
'l':['k'],
'm':['h']
}
def bfs(graph, start_node):
visited = [] #방문한 노드를 담을 리스트
queue = [] #방문 예정인 노드를 담을 배열
queue.append(start_node) #시작 노드 담기
while queue: #모든 노드를 방문 할 때까지 반복
node = queue.pop(0) #선입 선출인 큐의 구조를 이용해 앞에서 부터 꺼내기
if node not in visited: #이미 방문한 노드 x
visited.append(node) #방문 리스트에 담기
queue.extend(graph[node]) #스택에 해당 노드의 자식 노드들 추가
print(visited)
bfs(Graph, 'g')