회귀 모델중 규제를 통하여 variance를 줄이고 bias를 높여 미래 데이터에 대해 안정적인 결과를 도출하는 regularized linear regression 기법이 존재합니다.
해당 기법을 사용하는 모델에는 대표적으로 ridge와 lasso가 존재합니다.
이 두 모델은 rss에 norm을 더하는 방식을 사용해 계수에 규제를 가한다는 공통점이 존재합니다.
하지만 위 모델들은 규제를 가하는 방식에 차이가 존재합니다.
이번 글은 두 모델의 규제 방식의 차이에 관해 이야기 해보도록 하겠습니다.
Ridge 회귀의 규제 방식
릿지 회귀의 목적 함수는 다음과 같습니다.
다음은 목적 함수에 대한 설명입니다.
해당 부분은 rss에 관한 식으로
실제 값과 예측 값의 차이의 제곱으로 구성됩니다.
해당 부분은 L2 norm에 관한 식으로 회귀 계수인 베타의 크기를 제한하는 부분입니다.
여기서 람다는 규제의 강도를 조절하는 하이퍼 파라미터입니다.
L2 norm이란?
다음은 Lp norm에 관한 식입니다.
norm이란 선형대수에서 벡터의 크기를 알려주는 것입니다.
여기서 p값이 변함에 따라 L1 norm, L2 norm ... 등으로 불립니다.
따라서 L2 norm은 p가 2인 norm이 됩니다.

이제 rss와 l2 norm에 관한 설명을 마쳤으므로
릿지 회귀의 목적식을 기하학적으로 표현해보도록 하겠습니다.
릿지 회귀의 기하학적 표현
저희가 찾아야하는 최적의 계수를 베타1과 베타2로 두고 진행하도록 하겠습니다.
이 식을 전개하면
위와 같은 과정을 거쳐
이러한 형태의 식이 나오게 됩니다.
이 식은 2차식 형태로 원추 곡선의 형태를 가지게 됩니다.
따라서 rss를 표현한다면 타원의 형태가 나오게 됩니다.
추가적으로 릿지 회귀는 L2 norm을 더해주므로 L2 norm과 함께 시각화를 진행하도록 하겠습니다.
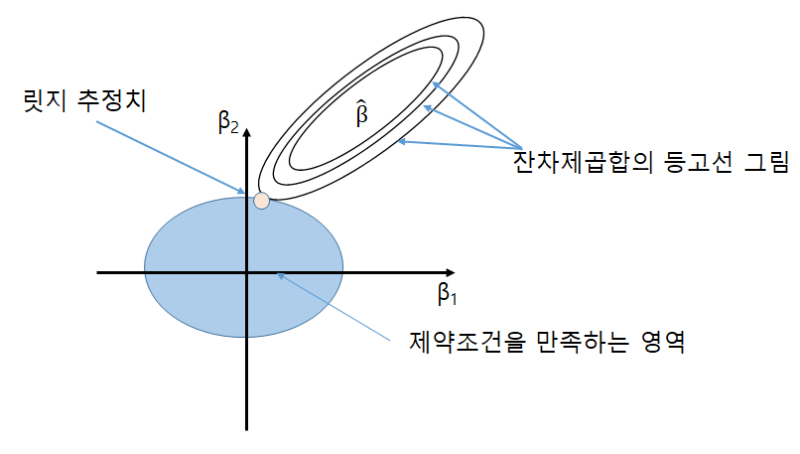
저희가 특정 람다를 지정하며 L2 norm이 특정한 수 이하가 되도록 제약을 가했다고 가정해 봅시다.
그러면 릿지 회귀는 이러한 제약을 만족하면서도 rss가 최소인 지점에 해당하는 두 베타 값을 찾을 것입니다.
따라서 제약 조건을 만족하는 영역과 rss가 최소인 지점의 교점으로 릿지 추정치를 설정합니다.
Lasso 회귀의 규제 방식
라쏘 회귀의 규제 방식은 릿지와 큰 차이가 없습니다.
하지만 rss에 L1 규제를 더한다는 부분에서 차이가 보입니다.
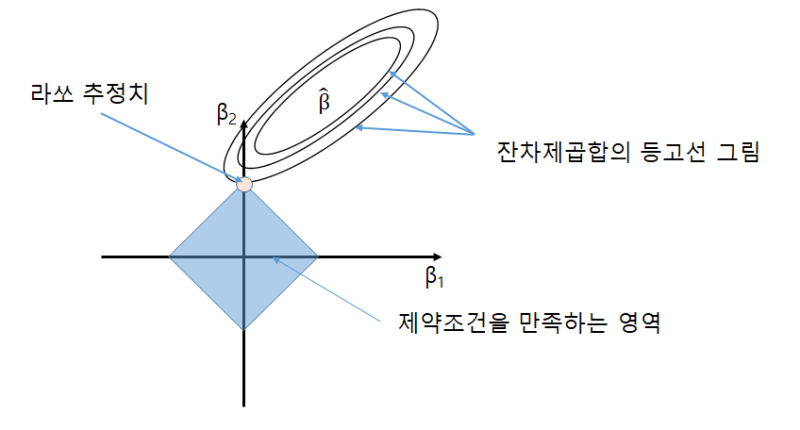
L1 규제를 적용했으므로 가운데 원 모양이 아닌 마름모 모양이 나타나는 것을 볼 수 있습니다.
위 그래프를 통해 알 수 있는 라쏘 회귀의 또 다른 특징은 계수를 0으로 설정 가능하다는 것 입니다.
릿지 모델인 경우 L2 규제를 적용하여 원 모양이 나와 제약 조건을 만족하며 rss가 최소인 지점의 값이 0이 나올 수 없는 구조입니다. 하지만 라쏘 모델은 마름모이므로 0인 지점이 나올 수 있습니다.
이상으로 포스팅을 마치겠습니다.
잘못된 부분이 존재한다면 댓글을 통해 자유롭게 피드백 부탁드립니다.
