
병합 정렬
분할정복 방법의 처리 과정: 분할 => 정복 => 병합.
분할=> 여러 작은 문제들로 분할.
정복=> 분할시킨문제들이 충분히 작아졌다면 문제에 대한 해를 구함.
결합=> 구한 해를 결합해서 원래 문제의 답을 구한다.
소스코드
public static int Solution(int [] arr,int left,int right){
if(left== right){
return arr[left];
}
int mid = (left+right)/2;
left = Solution(arr,left,mid);
right= Solution(arr,mid+1,right);
return (left > right) ? left :right;
}
최댓값 구할때 노드에 value와 next를 담아서 이차배열을 정렬
node class
class NodeDiv{
int value;
NodeDiv next;
NodeDiv(int value){
this.value =value;
this.next = null;
}
}링크드리스트 배열 만들기
public static void setUpLinkedList2(NodeDiv[] node, int[][] li){
for (int i = 0; i < li.length; i++) {
node[i]= new NodeDiv(li[i][0]);
//노드에 일단 value 넣고
}
for (int i = 0; i < li.length; i++) {
NodeDiv cur = node[i];
for (int j = 1; j <li[i].length ; j++) {
cur.next = new NodeDiv(li[i][j]);
cur = cur.next;
}
}
}만든 리스트를 분할
public static NodeDiv Solution(NodeDiv[] node) {
if (node == null || node.length == 0) {
return null;
}
return divided(node,0,node.length-1);
}
public static NodeDiv divided(NodeDiv[] node,int left, int right){
int mid = (left +(right-left))/2;
if(left == right){
return node[left];
}
NodeDiv N1 = divided(node,left,mid);
NodeDiv N2 = divided(node,mid+1,right);
return mergeNode(N1,N2);
}결합
public static NodeDiv mergeNode(NodeDiv l1, NodeDiv l2){
if(l1 == null){
//아무것도 없는 l1
return l2;
}
if(l2 == null){
return l1;
}
NodeDiv merge = new NodeDiv(0);
//새로운 병합 노드 merge
NodeDiv cur = merge;
// 현재 노드
while(l1 != null && l2 != null){
if(l1.value < l2.value){
cur.next =l1;
//오름차순이니깐
//li이 작은애
l1 = l1.next;
}else{
cur.next = l2;
//l2가 작을때
l2= l2.next;
}
cur = cur.next;
//그러고 cur 그다음 병합
}
if(l1 != null){
cur.next = l1;
}
if(l2 != null){
cur.next =l2;
}
return merge.next;
}
노드 출력 function
public static void printNodeList(NodeDiv node){
NodeDiv cur =node;
while(cur.next != null){
System.out.print(cur.value+" ->");
cur = cur.next;
}
System.out.println(cur.value);
}
main 함수
public static void main(String[] args) {
int [] arr ={5,4,6,7,3,1,2,3};
System.out.println(Solution(arr,0,arr.length-1));
int[][] lists = {{2, 3, 9}, {1, 5, 7}, {3, 6, 7, 11}};
NodeDiv[] node = new NodeDiv[lists.length];
//이걸 링크드리스트로 만든다 .
setUpLinkedList2(node, lists);
NodeDiv combine = Solution(node);
printNodeList(combine);
}
// 노드 관련 문제 풀이 프로세스
- 노드 클래스 생성.
- 링크드리스트 형식 노드리스트 구현.
- 분할, 정복 , 결합 과정 거쳐서 list 재 결합.
- 출력
퀵 정렬
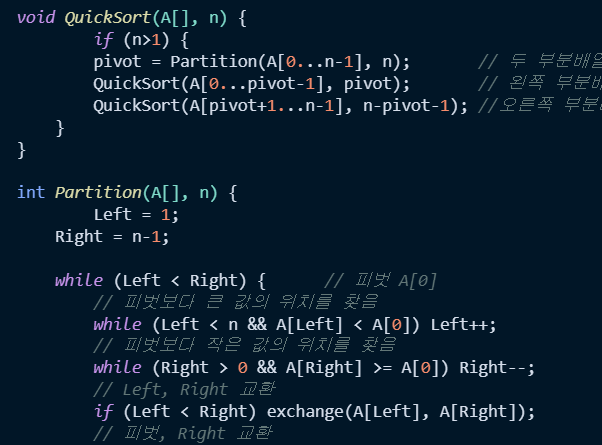
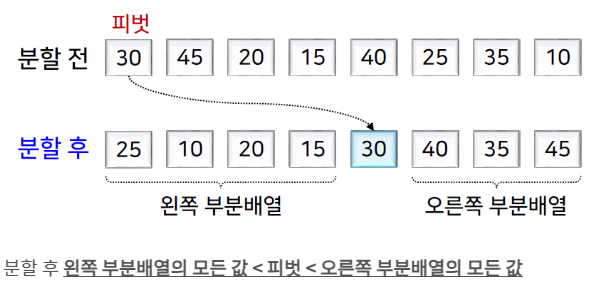
특정 원소 피벗(pivot)을 기준으로 주어진 배열을 두 부분배열로 분할하고 각 부분배열에 대해 퀵 정렬을 순환적으로 적용하는 방식
최선/평균 성능 Θ(nlogn)
- 최악 성능 Θ(n²)
퀵 정렬 분할정복 프로세스
분할 : 피벗을 기준으로 배열을 두 부분배열로 분할
정복 : 두 부분배열에 대해 퀵 정렬을 순환적으로 적용하여 각 부분배열을 정렬
결합 : 결합 불필요
퀵 정렬
public static void quickSort(int[] arr, int left, int right) {
if(left >= right){
return ;
}
int pivot = partition(arr,left,right);
quickSort(arr,left,pivot-1);
quickSort(arr,pivot+1,right);
}
정렬 안의 pivot을 구하는 partition
public static int partition(int[] arr, int left, int right) {
int pivot = arr[left];
int i = left;
int j = right;
while (i < j) {
while (arr[j] > pivot && i < j) {
//right
j--;
}
while (arr[i] <= pivot && i < j) {
//left
i++;
}
swap(arr,i,j);
//left, right 교환
// 안그럼 i<j여야하는데 아니면 while문에서 빠져나가야됨.
}
swap(arr,left,i);
//pivot과 i와 j가 만난 위치를 바꿔줌
// 그럼 i에 pivot이 들어감.
return i;
}이분탐색
T(n) = logn
정렬된 데이터를 효과적으로 탐색한다.
입력이 정렬되어야 함.
배열의 가운데 원소와 target 정수를 비교
1) target == mid => 탐색 성공.
2) target < mid => target이 mid 보다 작으므로 right = mid-1;
함수 호출 함수(arr,target,left,mid-1);
3) target>=mid => target이 mid보다 크거나 같다. left = mid+1;
함수(arr,target,mid+1,right);
로 구성.
풀이생각
- 결국 배열안의 특정 값을 찾는거다.
- target과 범위 배열을 만든다.
- 이분탐색을 돌린다.
반복문 구조
public static int binarySearch(int [] arr , int n){
int left = 0;
int right = arr.length-1;
while(left<= right){
int mid = (left+right)/2;
if(arr[mid]== n){
return mid;
}else if(n < arr[mid]){
right = mid -1;
}else{
left = mid+1;
}
}
return -1;
}
재귀 구조
public static int binarySearch2(int [] arr , int n ,int left,int right){
if(left>right){
return -1;
}
int mid =(left+right)/2;
if(n == arr[mid]){
return mid;
}else if(n < arr[mid]){
return binarySearch2( arr,n,left,mid-1);
//미드 오른쪽
}else{
//미드 왼쪽
return binarySearch2(arr,n,mid+1,right);
}
}
재귀가 좀더 편할지도?
문제 풀이 고민해보기