기초통계

Chapter 1 기초통계와 데이터 분석 기초

데이터의 종류

• Numerical(수치형)
  -> 수치 값으로 표현되는 데이터로 연속적 또는 이산적일 수 있음
  -> 예시) 연속적: 키, 몸무게, 온도 등, 이산적: 판매된 제품의 개수, 사람 수 등
  -> 분석방법: 중앙값, 평균, 표준편차 등의 통계적 수치를 사용하여 분석
  -> 시각화 방법: 히스토그램, 스캐터 플롯 등

• Categorical(범주형)
  -> 명확하게 분류 및 라벨링 될 수 있는 데이터
  -> 예시) 순서가 있는(Ordinal): 학력 수준, 순서가 없는(Nominal): 국적, 색상, 성별 등
  -> 분석방법: 각 카테고리의 빈도나 비율을 통해 분석
  -> 시각화 방법: 바 차트, 파이 차트, 스택 차트 등

• 분석기법: 데이터의 유형에 따라 분석방법이 다름

• 전처리: 데이터를 분석하기 전에 필요한 전처리 과정이 다름

• 시각화: 데이터의 유형에 따라 시각화 방법이 달라짐

지표(Metric)의 이해

• 모든 수치는 다 Metric이 될 수 있음

• Metric은 특정 현상 혹은 변화가 일어났을 때 Metric을 관찰함으로써 해당 현상의 핵심을 파악할 수 있도록 도움을 줌

• 사람들은 소비자물가지수를 확인함으로써 물가가 높아지는 상황에 대응하고, 물가가 낮아지는 시점을 예측 함

• Metric은 사람들이 관심을 두는 상황을 직관적으로 나타내며, 상황에 대한 대응을 도울 수 있음

• 증감율(%): 이전 기간 대비 현재 기간의 값이 얼마나 변화했는지 나타내는 비율
  
  -> 기존 값 대비 얼마나 변화했는지를 비율로 표현
  -> 특정 지표의 변동성이나 증감, 성장률을 표현
  -> 매출 성장률: 전년 대비 올해의 매출이 얼마나 성장했는지

• 퍼센티지 포인트(%p): 퍼센트의 증감을 나타내는 단위, 퍼센트 자체의 변화를 나타낼 때 사용
  -> 퍼센트 자체의 변화를 정확하게 표현하기 위해 사용
  -> 증감률과 혼동될 수 있는 상황에서 %p
  -> 시장 점유율(MS): MS가 전 우러 대비 20%에서 25%로 5%p증가

다양한 Domain Metric

• Ads: CTR, Cost per Acquisition, ROAS
• Streaming: DAU, Clicks, Time Spent, Retention
• Marketing: CAC, NPS, CLTV, Shares
• Finance: ROI, CAGR

기술통계량(Descriptive statistics)

• 데이터 분석의 기본 단계는 데이터의 전반적인 특성을 이해하는 것

• 기술통계량을 통해 데이터의 특징을 빠르게 파악하고, 분석의 방향성을 결정할 수 있음
  -> 어떤 제품의 월별 판매 데이터가 있을 때, 기술통계량을 사용하여 판매 추세, 이상치, 판매량의 변동 등을 빠르게 파악할 수 있음
  

• 평균(Mean): 자료 전체의 경향을 나타내는 값으로 가장 많이 이용됨
  -> 장점: 일반적인 대표값으로 손쉽게 데이터의 경향 파악 가능
  -> 단점: 극단적인 값에 영향을 받음

• 중앙값(Median): 크기 순으로 정렬한 데이터에서 중앙에 위치한 값
  -> 장점: 이상치에 대하여 강건함
  -> 단점: 자료의 수가 많아지면, 그 집단을 대표하는 대표성이 사라짐

• 최빈값(Mode): 가장 빈도가 많은 값
  -> 장점: 숫자로 나타내지 못하는 자료의 경우에도 구할 수 있음
  -> 단점: 자료의 개수가 적은 경우, 자료 전체의 특징을 반영하지 못할 수도 있음, 중복 발생

• 범위(Range): 변동성을 파악하기 위한 가장 쉬운 방법
  -> 장점: 간단히 계산 가능
  -> 단점: 데이터의 퍼진 특성들을 고려하기 어려움

• 분산(Variance): 범위의 단점을 보완, 데이터가 중심으로부터 얼마나 멀리 떨어져있는지를 계산
  -> 장점: 자료가 평균에서 얼마나 흩어져 있는지에 대한 대표값으로 사용할 수 잇음
  -> 단점: 제곱을 하여 계산하므로, 수치가 직관적이지 않음

• 표준편차(standard deviation): 분산에 루트를 씌어 자료의 단위와 동일하게 표현한 값
  -> 장점: 자료의 단위와 동일하여 직관적으로 해석하기 용이

• 왜도(skewness): 데이터의 비대칭도, 왼쪽이나 오른쪽으로 치우쳐진 정도

• 첨도(kurtosis): 데이터의 뾰족함, 높은 값은 더 많은 꼬리와 뾰족한 분포를 의미
  

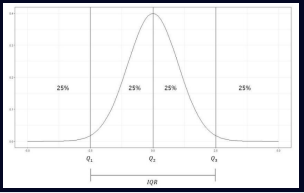
• 백분위수(Percentile): 전체 데이터 중 특정 백분율이 위치하는 값

• 4분위수(Quartile): 전체 관측값을 작은 순서로 배열했을 때, 전체를 사등분 하는 값
  

정규분포와 정규성 검증

• 통계적 분석의 기초
  -> 정규분포는 통계학에서 가장 기본적인 분포로, 많은 통계적 방법론과 기법들이 정규분포를 기반으로 함 -> 예를 들어, 표본의 평균을 추정하거나, 두 집단 간의 차이를 검정하는데 정규분포가 사용됨

• 중심극한정리의 이해
  -> 데이터 분석에서 중심극한정리는 매우 중요한 개념
  -> 큰 표본의 평균이 정규분포에 가까워진다는 것을 의미하며, 이는 다양한 데이터 분석 상황에서 통계적 추론의 근거가 됨

• 데이터 정규성의 검증
  -> 많은 통계적 테스트와 기법들은 데이터가 정규분포를 따른다는 가정 하에 개발됨
  -> 따라서 데이터가 이러한 가정을 만족하는지 검증하는 것은 분석의 정확성을 확보하는 데 중요

• 이상탐지 및 데이터 정제
  -> 정규분포를 이해하면 데이터 세트 내 이상치를 식별하고 처리하는 데 도움이 됨
  -> 표준편차를 기반으로 한 이상치 탐지는 많은 데이터 전처리 과정에서 핵심적인 부분

• 기계학습 알고리즘의 이해 및 적용
  -> 많은 기계학습 알고리즘들은 데이터가 특정 분포를 따른다고 가정
  -> 이러한 가정을 이해하고 검증하는 능력은 알고리즘의 선택과 성능 향상에 중요한 역할

• 실험 설계 및 결과 해석
  -> A/B 테스트와 같은 실험 설계 시, 정규분포는 실험 결과의 해석을 위한 기본적인 도구
  -> 실험 데이터의 분석과 해석에서 정규분포를 이해하는 것은 필수

• 통계적 추론(staticstical inference): 표본 데이터를 이용하여 모집단의 정보들을 추측하는 과정
  

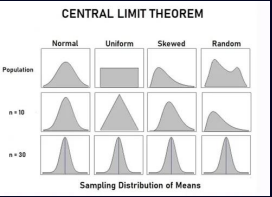
• 중심극한정리: 표본의 크기가 충분히 클 때, 여러 표본들의 표본평균이 이루는 분포가 정규분포에 가까워진다는 것
  

• 정규성 검정(Normality Test): 특정 데이터 세트가 정규분포를 따르는지 여부를 검증하는 과정으로 데이터가 정규분포를 따른다는 가정은 많은 통계적 방법론 및 기법들이 유효하게 작동하기 위한 전제 조건
  

Chapter 2 데이터의 관계를 파악하기 위한 기초분석

상관관계

• 상관분석
  -> 연속형 변수로 측정된 두 변수 간의 선형적 관계를 분석하는 기법
  -> A변수가 증가함에 따라 B변수도 증가되는지 혹은 감소하는지를 분석하는 것
  -> 선형적인 관계 정도를 나타내기 위해 상관계수(correlation coefficient)를 사용
  

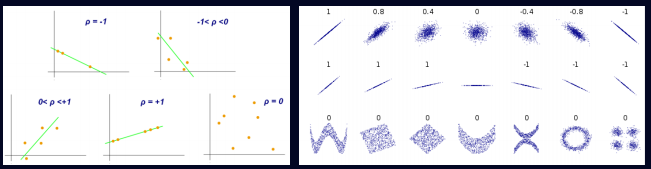
• 피어슨 상관계수(Pearson correlation coefficient)
  -> 두 변수의 선형 관계를 측정함
  -> 값을 -1에서 1 사이로 반환하며, 1은 완벽한 양의 선형 관계, -1은 완벽한 음의 선형 관계를 나타냄
  

회귀분석

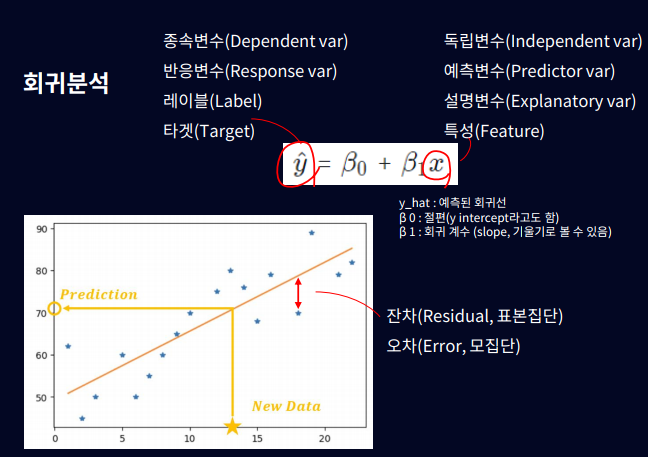
• 목표: 회귀 문제의 목표는 독립 변수(X)와 종속 변수(Y) 간의 관계를 모델링하여, 주어진 독립 변수에 대한 종속 변수의 값을 예측하는 것

• 원리: 선형 회귀는 독립 변수와 종속 변수 간의 선형 방정식을 찾아내는 방법으로, 주어진 데이터를 가장 잘 설명하는 최적의 회귀 계수 찾고 이를 통해 새로운 독립 변수 값에 대한 종속 변수 값을 예측할 수 있음

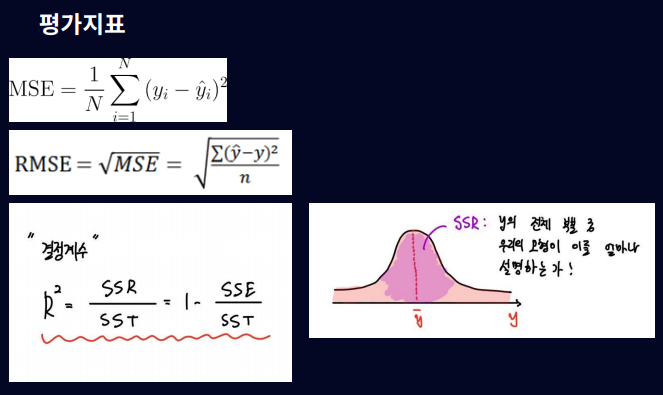
• Metric: 평균 제곱 오차(Mean Squared Error, MSE), MSE는 예측 값과 실제 값 사이의 차이를 제곱하여 평균한 값으로, 모델의 예측 정확도를 측정함. MSE가 작을수록 모델의 예측이 더 정확하다고 판단 R2 (R-squared) 값도 자주 사용되는 평가 지표. R-제곱은 종속 변수의 총 변동성 중 모델이 설명할 수 있는 변동성의 비율을 나타내며, 1에 가까울수록 모델이 데이터를 잘 설명한다고 판단됨

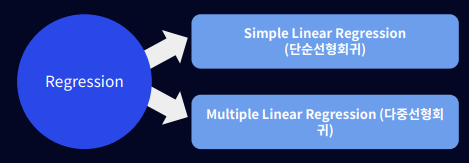
• 대표 알고리즘: 선형 회귀(Linear Regression), 다항 회귀(Polynomial Regression), 릿지 회귀(Ridge Regression), 라쏘 회귀(Lasso Regression), 엘라스틱넷(ElasticNet)

• 머신러닝(Machine Learning)의 가장 큰 목적은 실제 데이터를 바탕으로 모델을 생성해서 다른 입력 값을 넣었을 때 발생할 아웃풋을 예측하는데 있음

• 우리가 찾아낼 수 있는 가장 직관적이고 간단한 모델은 선(line)

• 데이터를 관찰하고 데이터를 잘 설명할 수 있는 선을 찾는 분석방법을 선형회귀(Linear Regression)라고 함
  

이 글은 제로베이스 강의 자료 일부를 발췌하여 작성되었습니다