👉 오늘 한 일

• 위클리 키워드 정리
• 미니 프로젝트 진행

키워드 : 분류손실함수

1. 손실함수란❓

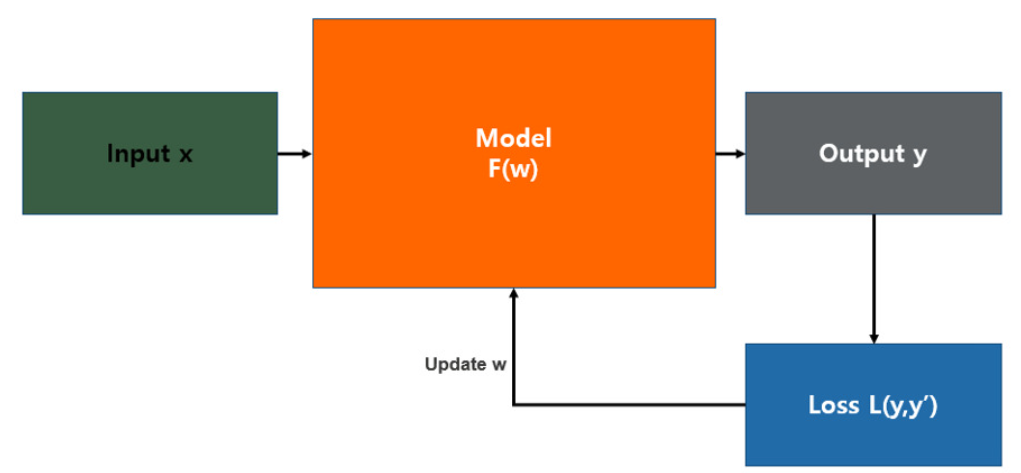
위의 그림은 일반적인 통계학적 모델의 형태로 입력 값이 들어오면 모델을 통해 예측 값을 산출되는 방식이다. 이 그림에서 예측 값이 실제 값과 얼마나 유사한지 판단하는 기준이 필요한데 그것이 바로 손실 함수(Loss Funstion)이다.

💡 손실함수(Loss Funstion): 머신러닝 혹은 딥러닝 모델의 예측값과 실제값의 차이를 수치화해주는 함수

즉, 손실 함수는 모델 최적화를 위해 반드시 사용되어야 하는 성능 평가 함수이다. 만약 실제 값과 예측 값의 차이가 크다면 오차가 크며, 손실 함수 값도 커지게 된다.

👉 다시 말하면, 손실 함수를 최소화 하는 적절한 모델을 찾는 것이 머신 러닝 또는 딥러닝의 목표가 될 수 있다.

통계학적 모델은 일반적으로 회귀(regression)와 분류(classification)으로 나눠지며, 손실함수도 이에 따라 두 종류로 나눠진다.

2. Cross Entropy

분류(Classification)에서 대표적으로 사용되는 손실 함수로 Cross-entropy방식이 있다.

💡 Cross-entropy: 실제 분포인 q 에 대해 알지 못하는 상태에서 모델링을 하여 구한 분포인 p분포를 통해 q 분포를 예측하고자 하는 것

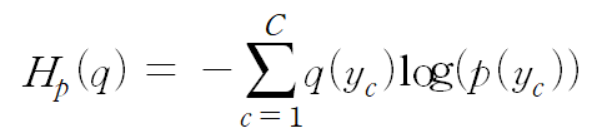
이 때, q와 p가 모두 식에 들어가기 때문에, Cross-entropy 라는 이름이 붙었다고 할 수 있다. 머신러닝 또는 딥러닝을 통한 예측 모형에서 훈련 데이터에서는 실제 분포인 p 를 알 수 있기 때문에 Cross-entropy를 계산할 수 있다. 즉, 훈련 데이터를 사용한 예측 모형에서 Cross-entropy 는 실제 값과 예측값의 차이 (dissimilarity) 를 계산하는데 사용할 수 있다는 것이다.

Cross-entropy는 예측 값이 실제 값에 가까울 경우 0에 수렴하며, 틀릴 경우에 값이 커지게 된다. 딥러닝을 통한 예측 모델링에 있어 실제 값과 예측 값의 차이를 계산한다는 관점에서 Cross-entropy를 사용하는 것의 의미를 직관적으로 이해해볼 수 있다.

🙌 간단히 구해보자!

import numpy as np
def CEE(y, t):
    delta = 1e-10
    return -np.sum(t*np.log(y+delta)) #CEE 계산식

t = np.array([0, 0, 0, 0.5, 0.5, 0, 0, 0, 0, 0]) #실제값
y0 = [0, 0, 0, 0.5, 0.5, 0, 0, 0, 0, 0] #예측값1
y1 = [0.01, 0.01, 0.1, 0.3, 0.33, 0.04, 0.02, 0.05, 0.01, 0.1] #예측값2
y2 = np.array([0.3, 0.01, 0.1, 0.01, 0.04, 0.02, 0.05, 0.33, 0.01, 0.1]) #예측값3

print(CEE(t,y0)) # 0.6931471803599453
print(CEE(t,y1)) # 8.265472039806522
print(CEE(t,y2)) # 21.21844021456322

위의 코드에서 볼 수 있는 것처럼 실제 값에서 예측 값이 멀어질수록 손실 값이 커짐을 알 수 있다.

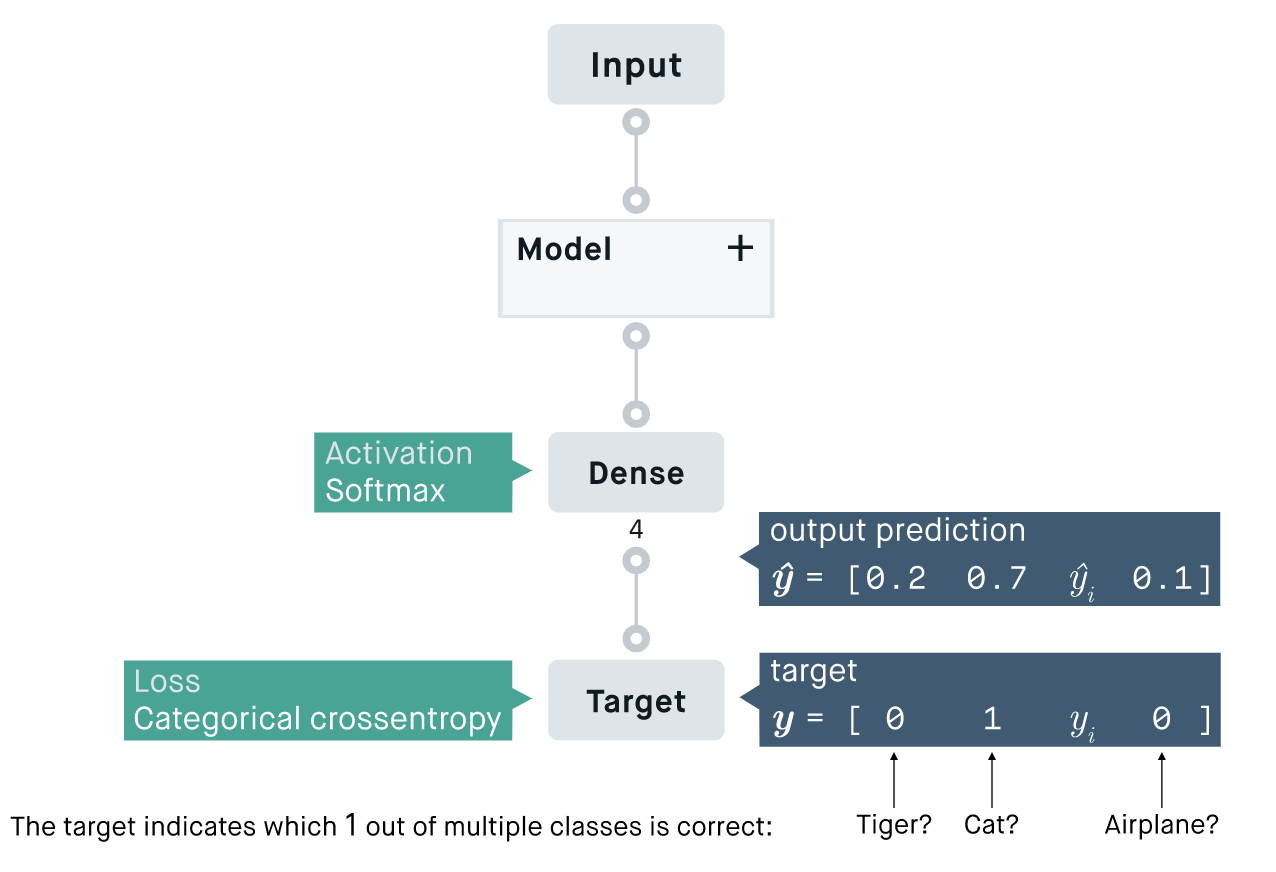
🙌 딥러닝 모델을 가정했을 때 Cross-entropy는 아래와 같은 과정으로 추출된다.

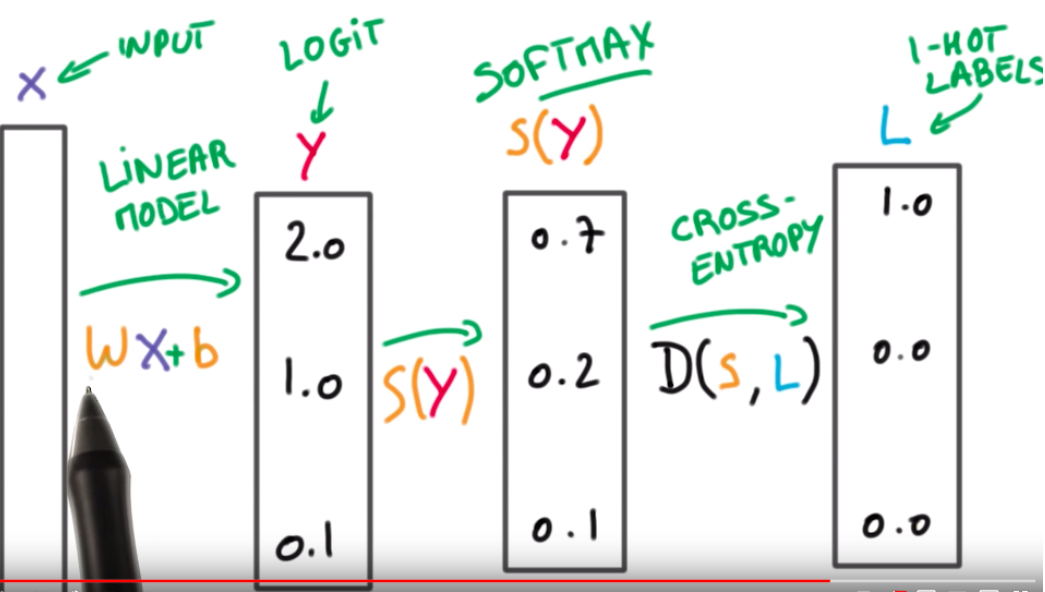
딥러닝 모델(Linear model)을 통해서 예측 값(logit, 또는 스코어)이 도출

→ Softmax 함수를 통해 이 값의 범위를 0~1로 조정하여 총 합이 1이되게 함

→ 정답 label과의 Corss-Entropy를 통해 loss 산출

(이 때, 정답 클래스에 해당하는 스코어에 대해서만 로그 합을 구해 최종 loss를 구함)

위 그림을 도식화 및 수식화 한 그림은 아래와 같다 👇

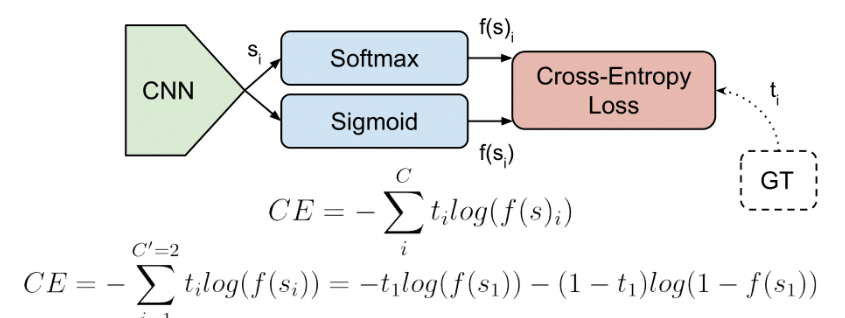
2.1. binary crossentropy : 이진 분류 모델에 사용

출처 : https://kh-kim.gitbook.io/natural-language-processing-with-pytorch/00-cover-7/06-multi_classification

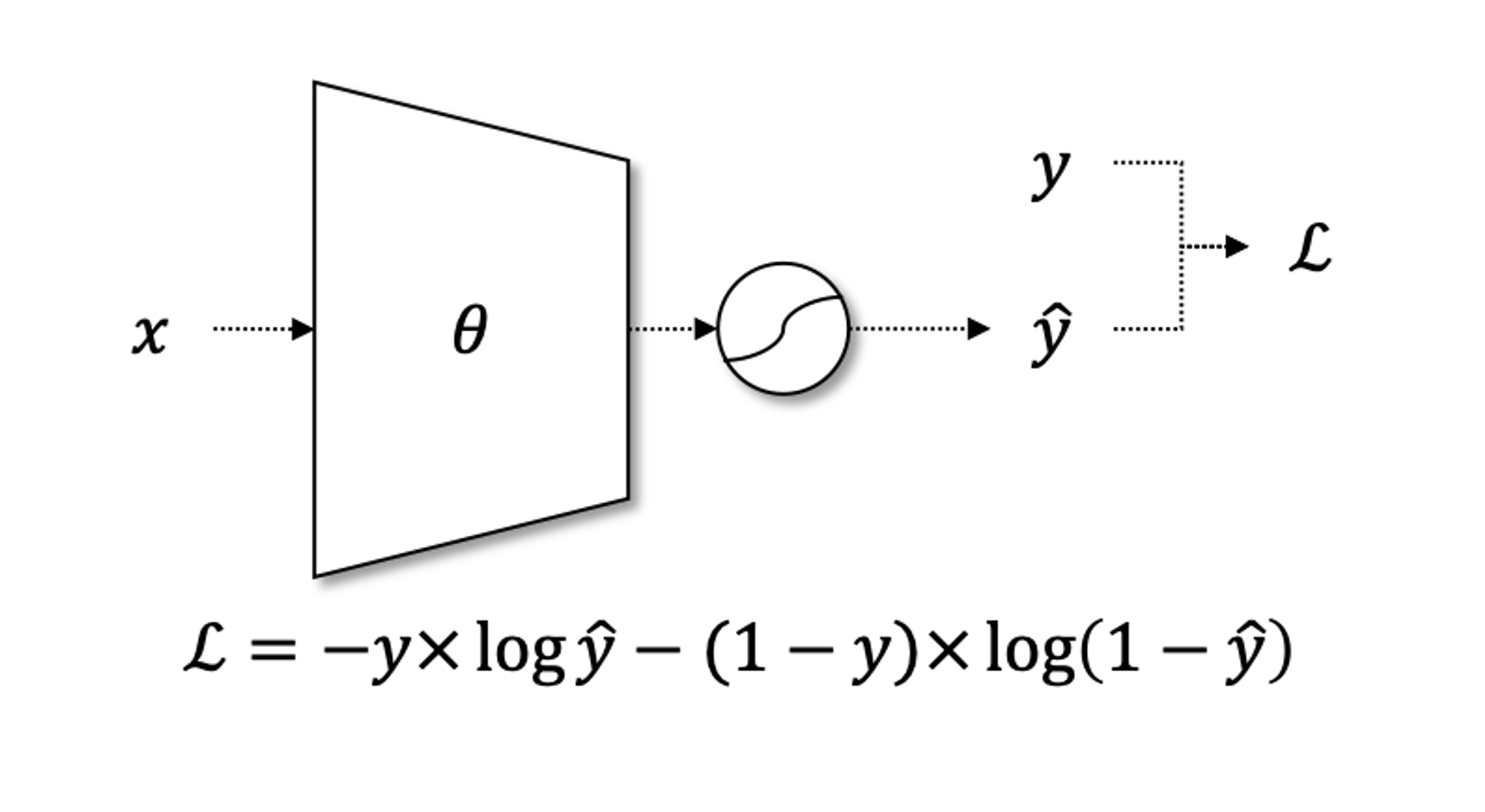
• 이진 분류 모델
  • True / False, 양성 / 음성 등 2개의 클래스를 분류할 수 있는 모델
  • 이진 분류 모델의 예측값은 0과 1 사이의 확률값
    예측값이 0에 가깝다면 False(혹은 True), 예측값이 1에 가깝다면 True(혹은 False)일 확률이 높음
• 함수식

출처 : https://towardsdatascience.com/understanding-pytorch-loss-functions-the-maths-and-algorithms-part-1-6e439b27117e

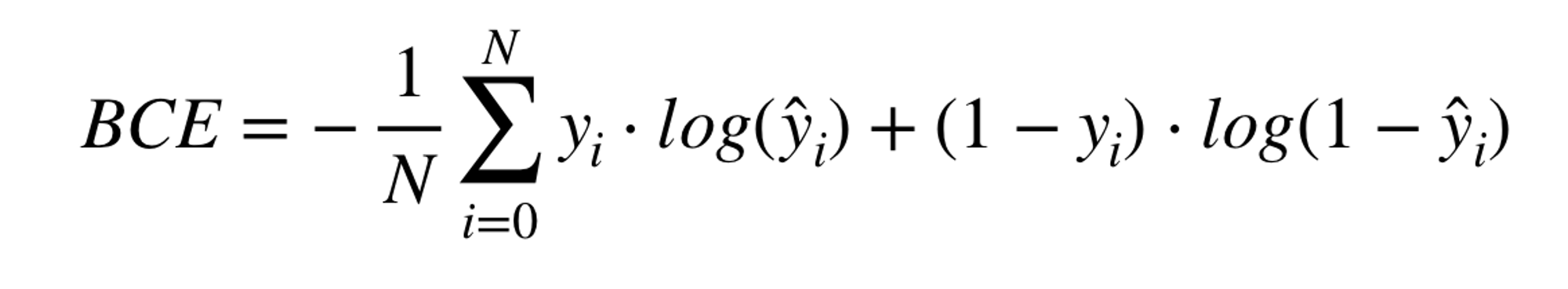
• Tensorflow 예시 코드
  

# 코드 출처 : https://www.tensorflow.org/api_docs/python/tf/keras/losses/BinaryCrossentropy
    
tf.keras.losses.BinaryCrossentropy(
        from_logits=False,
        label_smoothing=0.0,
        axis=-1,
        reduction=losses_utils.ReductionV2.AUTO,
        name='binary_crossentropy'
)

# 코드 출처 : https://siegel.work/blog/LossFunctions/
    
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding, LSTM, Bidirectional
    
#  this function builds, trains and evaluates a keras LSTM model 
def build_and_evaluate_model(x_train, y_train, x_develop, y_develop):
    
        x_train = sequence.pad_sequences(x_train, maxlen = 100)
        x_dev = sequence.pad_sequences(x_develop, maxlen = 100)
        
        model = Sequential()
        model.add(Embedding(input_dim = 10000, output_dim = 50))  #input_dim or the size of the data set, e.g vocabulary 
        model.add(Bidirectional(LSTM(units = 25)))
        model.add(Dense(1,activation='sigmoid'))
        model.predict(x_develop)
        model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics=['accuracy'])
        model.fit(x = x_train, y = y_train, batch_size = 32, epochs = 10, validation_data = (x_develop, y_develop))
        
        score, acc = model.evaluate(x_develop, y_develop)
     
        return score, acc, model

• 활성화 함수
  • y값(출력값)이 0에서 1 사이의 값인 sigmoid를 사용 → 이 때문에 binary crossentropy는 sigmoid crossentropy라 불리기도 함
    
  • 출력값이 0과 1 중 어디에 가까운지에 따라 이진 분류 가능
  • 다만 sigmoid 함수는 기울기 소실과 학습 속도 문제가 있으므로 출력층에서만 사용하는 것을 권장
  • 은닉층(입력층과 출력층 사이)에서는 사용하지 않는 것이 좋음
  • 입력층에서 sigmoid 함수를 사용하고자 한다면 sigmoid 함수를 일부 보완한 tahn(Hyperbolic Tangent) 함수를 대신 사용하는 것을 추천

2.2 categorical_crossentropy

Categorical Crossentropy : 레이블 (y) 클래스가 3개 이상일 경우 사용. 즉, 멀티클래스 분류에 사용

• 활성화 함수로 일반적으로 softmax 사용 (모든 벡터 요소의 값은 0과 1사이의 값이 나오고, 모든 합이 1이 됨)
• softmax 활성화 함수와 함께 쓰이는 경우가 많아 softmax loss 라고도 불림
• 라벨이 one-hot encoding 된 형태로 제공될 때 사용 가능
• 수식

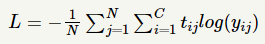
• C 는 클래스의 개수
• 실제값과 예측값이 모두 동일하게 될 경우 손실함수의 값은 0이 나옴

  • 샘플이 하나이고, 실제값과 예측값이 모두 [1 0 0 0 0]이라면

    $-(1log1 + 0log0 + 0log0 + 0log0 + 0log0) = 0$
• 실제값은 [1 0 0 0 0], 예측값은 [0 1 0 0 0]인 경우의 손실함수 값일 경우 양의 무한대로 발산

• 일반적으로 예측값은 [0.02 0.94 0.02 0.01 0.01]와 같은 식으로 나오기 때문에 양의 무한대가 나올리는 없지만, 큰 값이 나오게 됨
• 이러한 특성을 가지고 있기 때문에 멀티클래스 분류 문제의 손실함수로 사용

💡Categorical Crossentropy의 프로세스

💡 Tensorflow 예제 코드

• tf.keras.losses.CategoricalCrossentropy()

y_true = [[0, 1, 0], [0, 0, 1]]
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
# Using 'auto'/'sum_over_batch_size' reduction type.
cce = tf.keras.losses.CategoricalCrossentropy()
cce(y_true, y_pred).numpy()

>> 1.177

# 모델 컴파일 시에도 loss function으로 사용
model.compile(optimizer='sgd',
              loss=tf.keras.losses.CategoricalCrossentropy())

💡keras.categorical_crossentropy() 소스 코드

def categorical_crossentropy(
    y_true, y_pred, from_logits=False, label_smoothing=0.0, axis=-1
):
    if isinstance(axis, bool):
        raise ValueError(
            "`axis` must be of type `int`. "
            f"Received: axis={axis} of type {type(axis)}"
        )
    y_pred = tf.convert_to_tensor(y_pred)
    y_true = tf.cast(y_true, y_pred.dtype)
    label_smoothing = tf.convert_to_tensor(label_smoothing, dtype=y_pred.dtype)

    def _smooth_labels():
        num_classes = tf.cast(tf.shape(y_true)[-1], y_pred.dtype)
        return y_true * (1.0 - label_smoothing) + (
            label_smoothing / num_classes
        )

    y_true = tf.__internal__.smart_cond.smart_cond(
        label_smoothing, _smooth_labels, lambda: y_true
    )

    return backend.categorical_crossentropy(
        y_true, y_pred, from_logits=from_logits, axis=axis
    )

• logit옵션이 기본적으로 False이며 return값은 nagative likelihood 임
• output sum을 1로 scaling 해주긴 하지만, 확률값으로의 변환은 따로 없기 때문에 multiclass classification 문제를 해결하고자 한다면 마지막에 softmax를 해주어야 함.
  • from_logits=True로 하면 softmax 가 자동으로 적용

2.3 sparse_categorical_crossentropy

🍙tensorflow

**y_true = [1, 2]**
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
loss = tf.keras.losses.sparse_categorical_crossentropy(y_true, y_pred)
assert loss.shape == (2,)
loss.numpy()
# array([0.0513,2.303],dtype=float32)

: categorical_crossentropy와 똑같이 손실함수로 쓰이지만, 비교하는 값이 정수(int)로 사용된다.

• y_train이 범주의 인덱스로 되어 있을 때(one-hot-encoding안된다)사용
• 각 샘플이 정확히 하나의 클래스에 속한 경우에 사용이 좋다.
• 단점 : 정확도가 categorical_crossentropy와 차이가 없다.
• 장점 : 메모리 소요가 적다.
• 문자열 : "sparse_categorical_crossentropy”
• 함수 : tf.keras.losses.sparse_categorical_crossentropy
• 클래스 : tf.keras.losses.SparseCategoricalCrossentropy

3. Hinge loss

• 생긴게 경첩(hinge) 같다고 해서 붙여진 이름이다.
• 학습데이터 각각의 범주를 구분하면서 데이터와의 거리가 가장 먼 결정경계(decision boundary)를 찾기 위해 고안된 손실함수로 SVM(Support Vector Machine) 알고리즘을 위한 손실 함수로도 사용된다.
• Sj는 ‘정답이 아닌’ 클래스의 점수, Syi는 ‘정답’ 클래스의 점수, 1은 safty margin이다.
  • Sj - Syi + 1 > 0 일 경우 그 값이 loss가 된다.
  • Sj - Syi + 1 < 0 일 경우 loss는 0이 된다.

예를 들어 이미지를 분류하는 어떤 알고리즘이 고양이 이미지에 대해 스코어가 위와 같이 나왔다고 하자.

고양이 이미지에 대한 정답 클래스의 점수 즉 cat 클래스의 점수는 3.2이, 정답이 아닌 car 클래스는 5.1, frog 클래스는 -1.7 이다.

여기서 힌지 로스를 구해보자면 식은 아래와 같다.

max(5.1 - 3.2 +1) + max(-1.7 -3.2 + 1) 
= 2.9 + 0 = **2.9**

car 클래스에 대한 loss : car 점수 - cat 점수 + 1은 2.9로 0보다 크기 때문에 loss 값이 된다.

frog 클래스에 대한 loss : frog 점수 - cat 점수 + 1은 -3.9로 0보다 작기 때문에 loss 값은 0이 된다.

최종적으로 두 값을 더해 고양이 이미지의 loss는 2.9가 된다.

동일한 방식으로 loss 값을 구한 뒤 class의 수로 나누어 최종 loss는 5.27이 된다.

(2.9 + 0 + 12.9) / 3 = **5.27**

이것을 코드로 나타내면 다음과 같다.

def L_i_vectorized(x, y, w):
    scores = w.dot(x)
    margins = np.maximum(0, scores - scores[y] + 1)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i

만약 자동차 이미지의 car 클래스 점수가 4.9에서 3.9가 되더라도 cat 클래스 점수나 frog 클래스 점수보다 1 이상 높기 때문에 여전히 loss는 0이다.

즉, 이것은 Hinge loss가 데이터에 둔감하다는 뜻으로 점수가 몇점이냐보다 정답 클래스의 점수가 정답이 아닌 클래스의 점수보다 높은가에 관심이 있다는 뜻이다.

또 loss의 최소값은 언제나 0이다. 0보다 작을 경우 0을 loss 값으로 가져오기 때문이다.

반면 최대값은 이론상 무한정 증가할 수 있다는 특징이 있다.

미니 프로젝트

주제 : 월간 데이콘 신용카드 사용자 연체 예측 AI 경진대회
https://dacon.io/competitions/official/235713/overview/description

구글 colab 경로 확인 : %pwd

구글 드라이브에 마운트

• 이 방식 말고 직접 코랩에서 드라이브에 마운트해도 됨

from google.colab import drive
drive.mount('/content/drive')

• 마운트 한 후에 content/drive 경로를 보면 MyDrive가 생성되어 있음. 이제 내 드라이브에서 경로 지정하면 됨

# 구글 드라이브 내 데이터 경로 지정
path = '/content/drive/MyDrive/Colab Notebooks/data/credit_delinquency/'
path