👉 오늘 한 일

• 미니 프로젝트 마무리

Mini_project 5

월간 데이콘 신용카드 사용자 연체 예측 AI 경진대회

• https://dacon.io/competitions/official/235713/overview/description

배경

신용카드사는 신용카드 신청자가 제출한 개인정보와 데이터를 활용해 신용 점수를 산정합니다. 

신용카드사는 이 신용 점수를 활용해 신청자의 향후 채무 불이행과 신용카드 대급 연체 가능성을 예측합니다. 

현재 많은 금융업계는 인공지능(AI)를 활용한 금융 서비스를 구현하고자 합니다. 



신용카드 사용자들의 개인 신상정보 데이터로 사용자의 신용카드 대금 연체 정도를 예측할 수 있는 

인공지능 알고리즘을 개발해 금융업계에 제안할 수 있는 인사이트를 발굴해주세요!

목적

• 신용카드 사용자 데이터를 보고 사용자의 대금 연체 정도를 예측하는 알고리즘 개발

평가지표

• logloss
• Private Score를 기준으로 최종 순위를 결정

데이터 설명

출처 : https://www.dacon.io/competitions/official/235713/talkboard/402821/

index
gender: 성별
car: 차량 소유 여부
reality: 부동산 소유 여부
child_num: 자녀 수
income_total: 연간 소득
income_type: 소득 분류
							['Commercial associate', 'Working', 'State servant', 'Pensioner', 'Student']

edu_type: 교육 수준
							['Higher education' ,'Secondary / secondary special', 'Incomplete higher', 'Lower secondary', 'Academic degree']

family_type: 결혼 여부
							['Married', 'Civil marriage', 'Separated', 'Single / not married', 'Widow']

house_type: 생활 방식
							['Municipal apartment', 'House / apartment', 'With parents',

							 'Co-op apartment', 'Rented apartment', 'Office apartment']

DAYS_BIRTH: 출생일
							데이터 수집 당시 (0)부터 역으로 셈, 즉, -1은 데이터 수집일 하루 전에 태어났음을 의미

DAYS_EMPLOYED: 업무 시작일
							데이터 수집 당시 (0)부터 역으로 셈, 즉, -1은 데이터 수집일 하루 전부터 일을 시작함을 의미

							양수 값은 고용되지 않은 상태를 의미함

FLAG_MOBIL: 핸드폰 소유 여부
work_phone: 업무용 전화 소유 여부
phone: 전화 소유 여부
email: 이메일 소유 여부
occyp_type: 직업 유형													
family_size: 가족 규모
begin_month: 신용카드 발급 월
							데이터 수집 당시 (0)부터 역으로 셈, 즉, -1은 데이터 수집일 한 달 전에 신용카드를 발급함을 의미

credit: 사용자의 신용카드 대금 연체를 기준으로 한 신용도
							=> 낮을 수록 높은 신용의 신용카드 사용자를 의미함

📌모델 성능 개선을 위해 진행해 본 것

• 원핫인코딩이나 결측치 대체 등의 전처리를 하였습니다.

• 레이어의 갯수를 변경하였습니다.

• units의 갯수를 변경하였습니다.

• 활성화 함수를 변경하였습니다.

• dropout을 적용하였습니다.

• epoch수를 변경하였습니다.

• validation_split를 조정하였습니다.

• early_stop을 추가하였습니다.

후기

💡프로젝트를 진행하며 어려웠던 점이 있었다면?

• 딥러닝 파라미터 튜닝 방법을 잘 몰라서 일일히 손으로 코드를 바꿔가며 작업했는데.. 굉장히 오래 걸린다.

💡프로젝트를 진행하며 시도했지만 성공하지 못한게 있다면?

• 모델이 학습할 때 초기 가중치(랜덤값)에 영향을 많이 받는 것 같아서 초기 가중치를 고정시키고 학습해보려고 했으나 시간 관계 상 하지 못했다. 다음 미니 프로젝트 때 시도해보고자 한다.

💡프로젝트를 진행하며 배운 내용과 의견은?

• 딥러닝의 학습율 조정 방법과 그 외 성능 개선을 위한 파라미터 튜닝 방법을 알았지만, 이 데이터셋에는 부스팅 계열 머신러닝 모델이 성능이 더 좋았을 것 같다..!

💡딥러닝은 무엇인가? 딥러닝과 머신러닝의 차이는?

• 머신러닝은 사람이 직접 특징을 도출할 수 있게 설계해서 예측값을 출력하는 알고리즘이고,
• 딥러닝은 인공지능 스스로 일정 범주의 데이터를 바탕으로 공통된 특징을 도출하고, 그 특징으로 예측값을 출력하는 머신러닝 알고리즘의 한 분야 입니다.

💡알고있는 Activation Function은?(Sigmoid, ReLU, LeakyReLU, Tanh 등)

출처
https://deepinsight.tistory.com/113
https://yeomko.tistory.com/39

• 입력 신호의 총합을 출력신호로 변환하는 함수를 일반적으로 Activation Function이라고 합니다.(입력 신호의 총합이 활성화를 일으키는지 정하는 역할을 함)

1. Sigmoid
   특징

• 출력 값을 0에서 1로 변경해줍니다.(Squashes number to range [0, 1])
• 가장 많이 사용되었던 활성화 함수라고 합니다.

단점

• Saturation(포화상태)
  

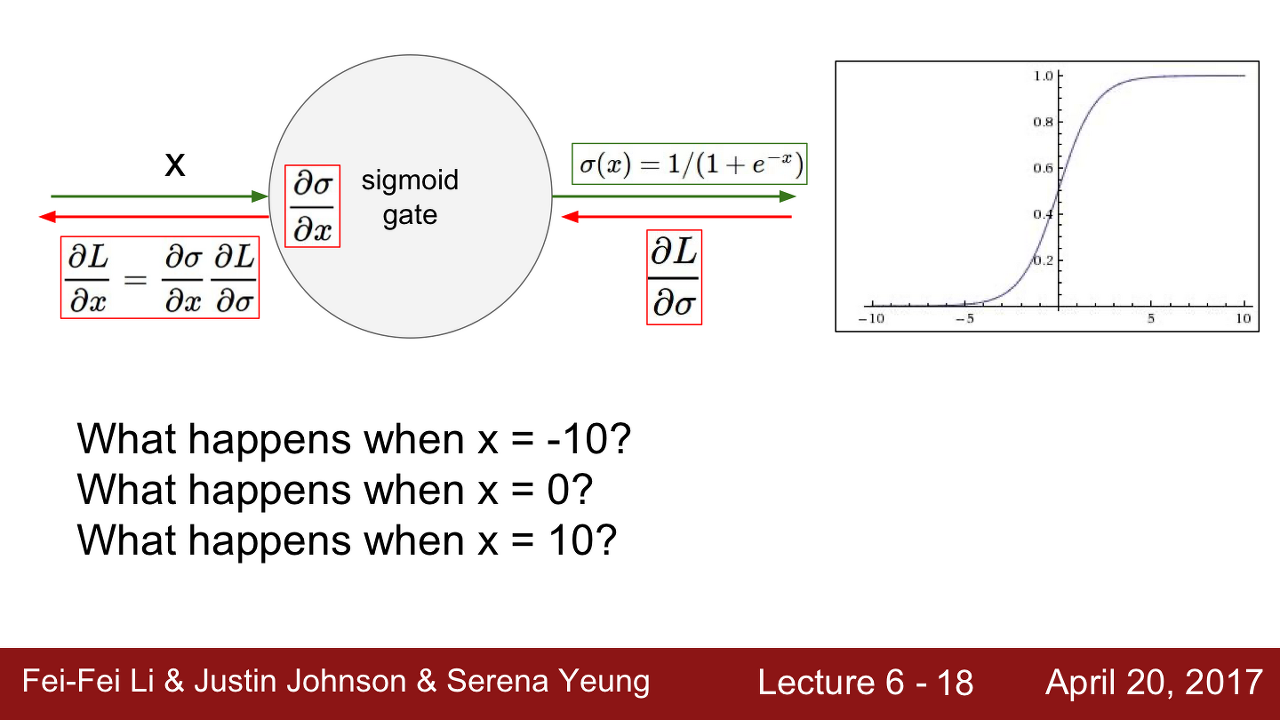
  • sigmoid 함수의 출력 그래프를 보면 입력 신호의 총합이 크거나 작을 때 기울기가 0에 가까워지는 것을 볼 수 있습니다. 이렇듯 Activation Function의 구간에서 기울기(gradient)가 0에 가까워지는 현상을 Saturated라고 합니다. 이는 Vanishing Gradient문제를 야기합니다.

• Sigmoid outputs are not zero-centered
  

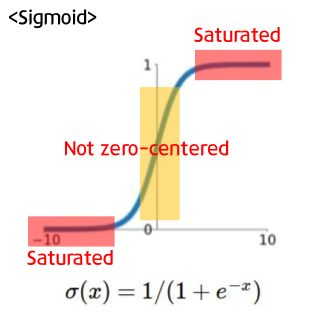
  • 만약 neuron의 input값인 x가 항상 양수라면 gradient W는 항상 양수이거나/항상 음수 일 것입니다

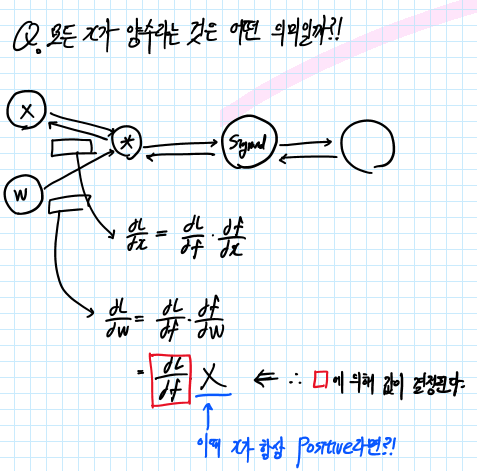
• W의 Gradient를 구하는 과정을 Computational Graph를 통해 알아보도록 합니다. 위의 그림과 같이 Loss에 대한 W의 Gradient는 Upstream Gradient(dL/df)에 Local Gradient(df/dW)를 통해 구할 수 있습니다. 이때 df/dW는 X와 같습니다. (곱셈에 대한 역전 파는 반대 값을 곱해주는 것과 같기 때문입니다.)
• 따라서 X의 값이 항상 Positive(+) 라면 dL/dW의 값은 Upstream Gradient(dL/df)의 값에 따라 정해지게 됩니다. 따라서 Gradient W의 값은 항상 Positive 또는 Negative 값이 됩니다. 이 말인즉슨 gradient W는 항상 같은 방향으로 움직인다는 것을 의미합니다.

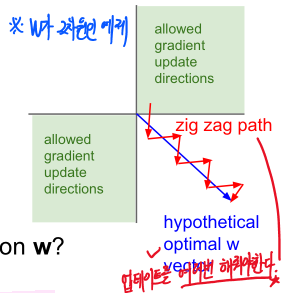
• (X가 항상 Positive라고 가정했을 때) W의 gradient는 항상 Positive 또는 Negative였습니다.

• (2차원의 W값이 있다고 가정을 해보겠습니다. x축을 w1, y축을 w2로 가정합니다.)

• 이때 W의 Update는 w1이 증가했을 때 w2도 증가하는 경우, w1이 감소했을 때 w2도 감소하는 두 가지 경우에 따라 Update 됩니다. (* 왜냐하면 W의 gradient(기울기)가 X가 항상 Positive일 때 항상 Positive or Negative 였기 때문입니다)

• 그런데 최적의 해가 w1이 증가했을 때 w2는 감소하는 방향입니다.(위의 그래프에서 파란색 직선)

• W의 gradient가 항상 Positive or Negative인 경우는 비효율적으로 최적해를 탐색하게 됩니다.

• 위의 그림과 같이 파란색 직선으로 해를 탐색하는 것이 아닌 'zig zag'로 해를 탐색하게 되는 것입니다. 여러 번 탐색을 해야 하기 때문에 비효율적인 weight update방법이 됩니다.

• 이것이 바로 우리가 일반적으로 zero-mean data를 원하는 이유입니다.

• 입력 X가 양수/음수를 모두 가지고 있으면 gradient w가 전부 Positive/Negative로 움직이는 것을 막을 수 있습니다.

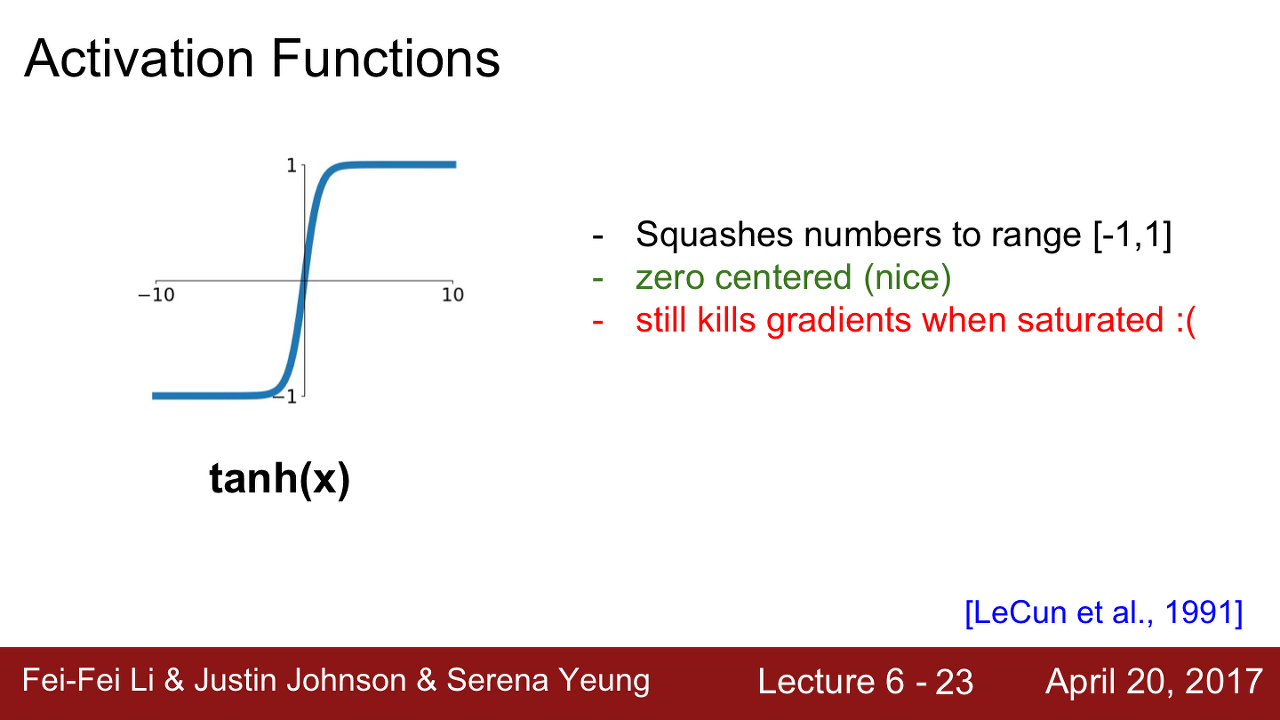
2. tanh
   특징

• 출력 값을 -1에서 1로 압축시켜줍니다.
• zero-centerd 합니다(sigmoid가 가졌던 두 번째 문제점을 해결해줍니다)

단점

• 여전히 gradient가 죽는 구간이 있습니다. (양수/음수 구간 모두 존재합니다)

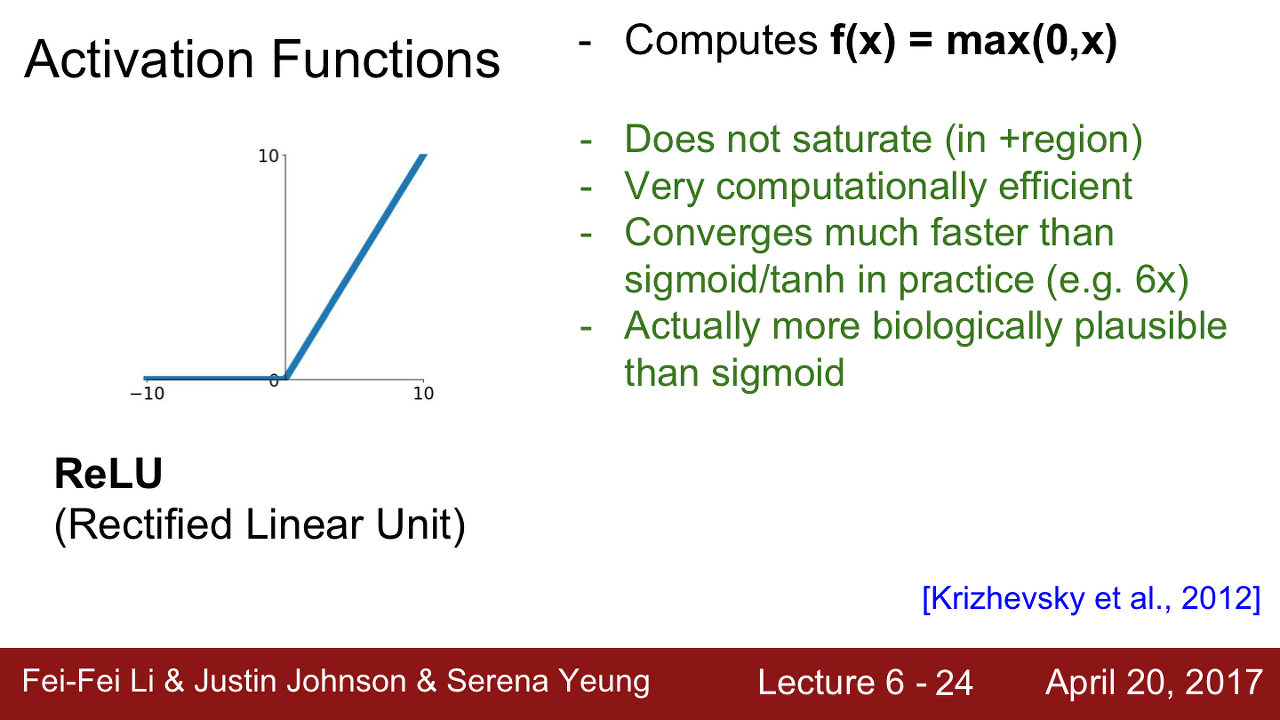
3. ReLU
   특징

• 양의 값에서는 Saturated 되지 않습니다.
• 계산 효율이 뛰어납니다. sigmid/tanh보다 훨씬 빠릅니다.(6배 정도)
• 생물학적 타당성도 가장 높은 activation function이라고 합니다.

단점

• zero-centerd가 아니라는 문제가 다시 발생했습니다.(non-zero centered)
• 또한 음수 영역에서 saturated 되는 문제가 다시 발생합니다.
  

Dying ReLU

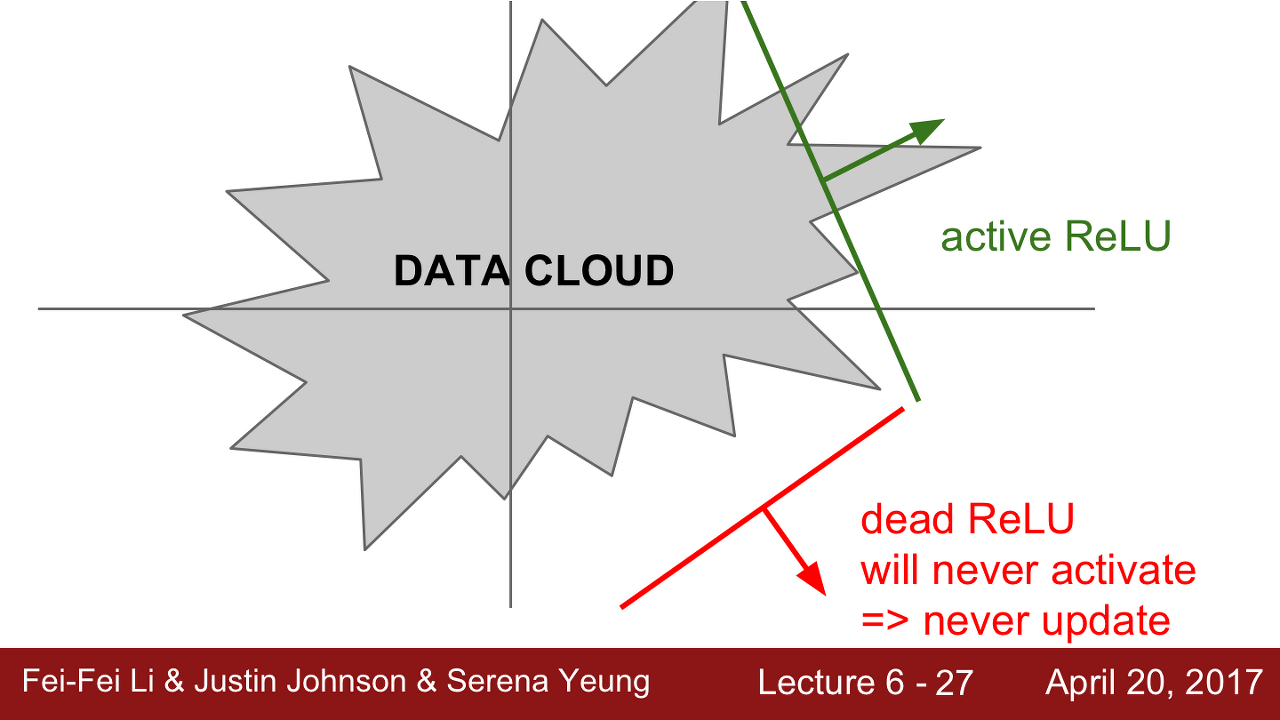
DATA CLOUD로부터 떨어져 있을 때 Dying ReLU가 발생할 수 있습니다.

1) 첫째, 초기화를 잘못한 경우입니다.

• 가중치 평면이 data cloud에서 멀리 떨어져 있는 경우입니다. 이런 경우 어떤 입력 데이터에서도 activate 되지 않습니다.

2) 더 흔한 경우는 Learning rate가 높은 경우입니다.

• 가중치 파라미터 업데이트의 learning rate가 높은 경우 ReLU가 데이터의 manifold를 벗어나게 됩니다. 이런 일들은 학습과정에서 흔한 일이고 충분히 발생할 수 있다고 합니다.

• 그래서 학습이 잘 되다가 죽어버리게 된다고 합니다.

🤔그렇다면 data cloud에서 ReLU가 죽어버리는지 아닌지를 어떻게 알 수 있을까요?

위의 예를 다시 보겠습니다. 간단한 2차원의 예를 통해 알아보도록 하겠습니다. 이때 가중치는 초평면(active ReLU 또는 dying ReLU)을 이루게 될 것입니다.

W의 초평면의 위치와 Data의 위치를 고려했을 때 W의 초평면 자체가 Data와 동떨어지는 경우가 발생할 수 있습니다.

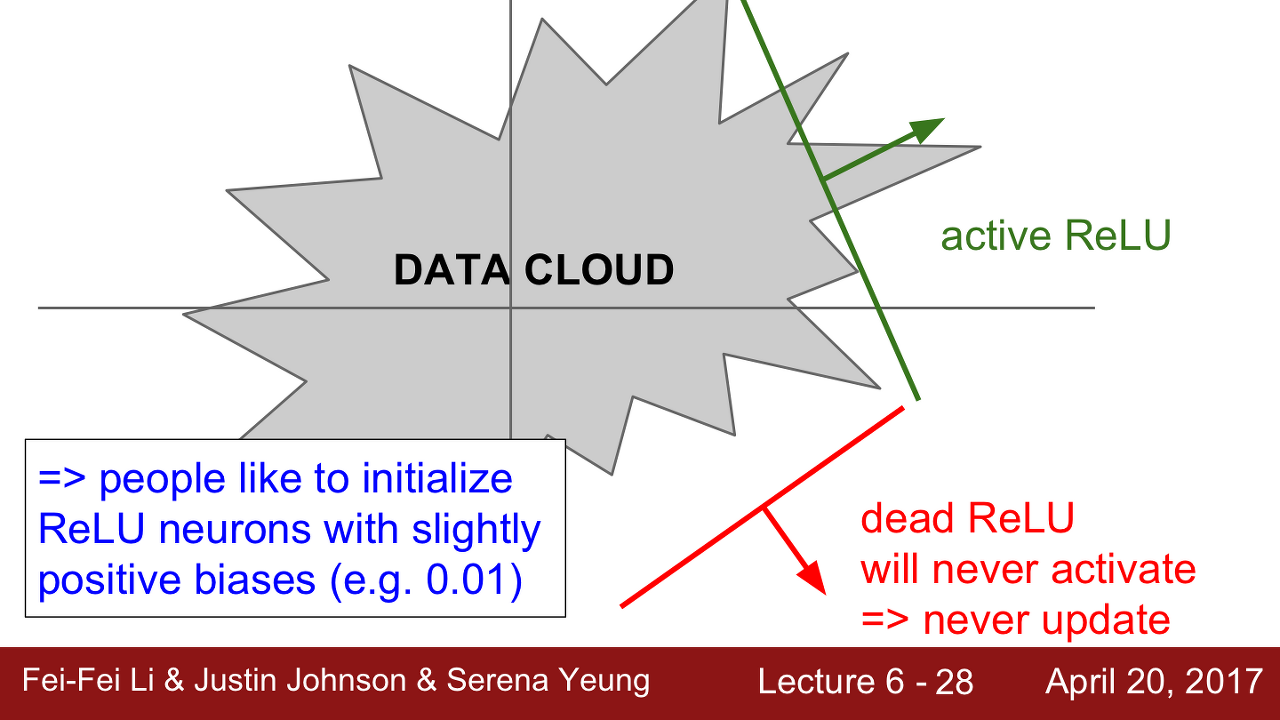
Dying ReLU를 피하기 위해 실제로 ReLU를 초기화할 때 positive biases를 추가해 주는 경우가 있습니다. Weight Update시에 active ReLU가 될 가능성을 조금이라도 늘려주기 위함입니다.

하지만 이 방법이 도움이 된다는 주장도 있고 도움이 되지 않는다는 주장도 있다고 합니다.

4. Leaky ReLU

특징

• ReLU와 유사하지만 negative regime(음의 영역)에서 더 이상 0이 아닙니다.
• saturated 되지 않습니다
• 여전히 계산이 효율적이며 빠릅니다
• 더 이상 Dying ReLU 현상이 없게 됩니다

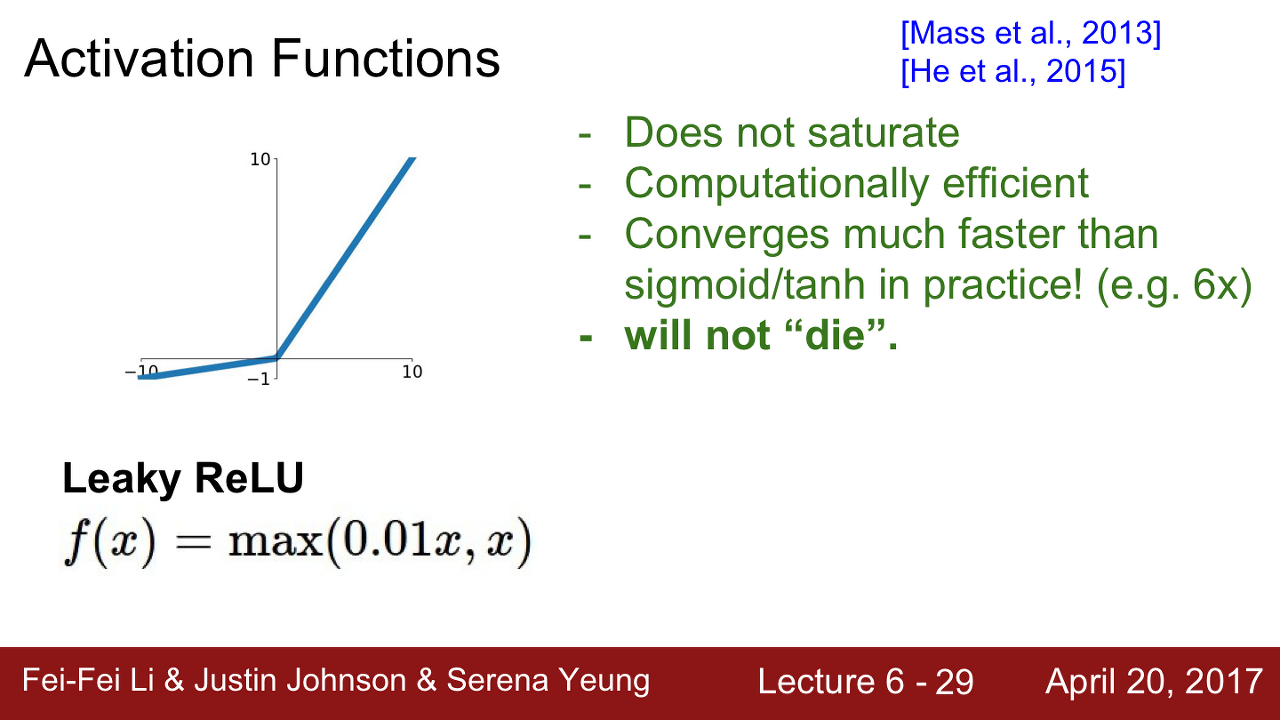
5. ELU(Exponential Linear Units), SeLU(scaled exponential linear unit)
   

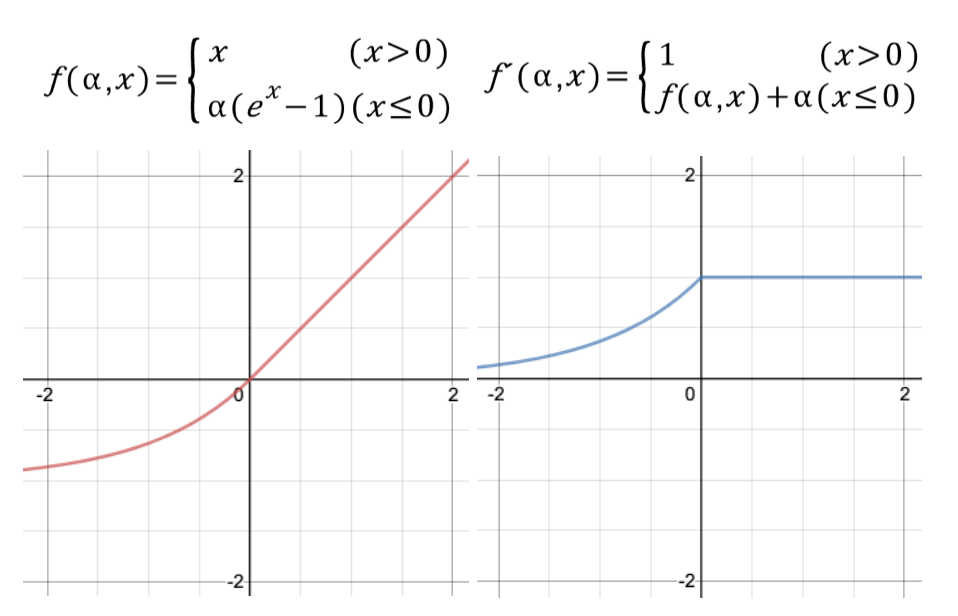
특징

• zero-mean에 가까운 출력 값을 보입니다.(그래프를 보시면 0을 기준으로 조금 스무스합니다)

• ReLU, LeakyReLU, PReLU가 zero-mean 출력 값을 갖지 못하는 것에 비해 상당한 이점을 가지고 있습니다.

• ReLU와 Leaky ReLU의 중간 정도라고 보시면 된다고 합니다. ELU는 Leaky ReLU처럼 zero-mean의 출력을 내지만 Saturation관점에서는 ReLU의 특성도 가지고 있습니다. -> 단점

• 지수 함수를 이용하여 입력이 0 이하일 경우 부드럽게 깎아줍니다. 미분 함수가 끊어지지 않고 이어져있는 형태를 보입니다. 별도의 알파 값을 파라미터로 받는데 일반적으로 1로 설정됩니다.

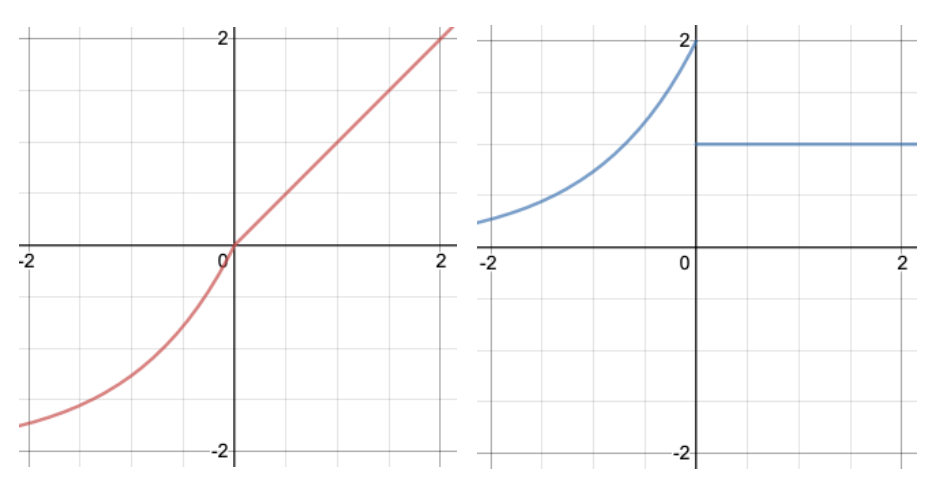
• 그 밖의 값을 가지게 될 경우 SeLU(scaled exponential linear unit)이라 부릅니다. 알파를 2로 설정할 경우 그래프는 아래와 같은 모습을 보입니다.
  

그 외 Swish, Softsign, Softplus, ThresholdReLU(thresold rectified linear unit), Maxout Neuron 등등.. 너무 많습니다...

💡기울기 소실 문제는 왜 발생할까?

• 기울기 소실 문제(Vanishing Gradient problem)는 역전파(Backpropagation) 알고리즘에서 처음 입력층(input layer)으로 진행할수록 기울기가 점차적으로 작아지다가 나중에는 거의 기울기의 변화가 없어지는 문제입니다.

  • 활성화 함수(Activation function)로 시그모이드 함수(sigmoid function)을 사용할 때 이 함수의 특성으로 인해 기울기 소실 문제가 발생합니다.
    

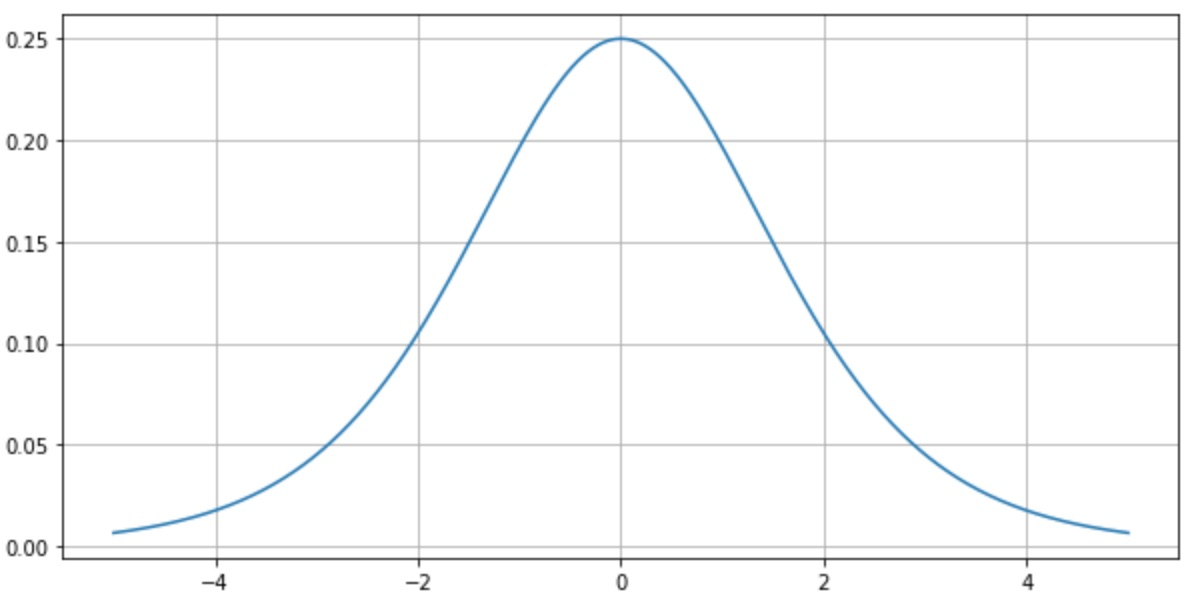
  • sigmoid 함수를 미분한 함수의 그래프를 보면 기울기가 최대가 0.25이고 최소가 0에 수렴합니다. 즉, 0 ~ 0.25사이의 값을 가집니다. 역전파에서 입력층에 가까운 앞쪽의 layer로 갈수록 sigmoid 함수의 미분을 연쇄적으로 곱하는데 기울기가 1보다 작으므로 곱할수록 값은 점점 작아지게 됩니다.

  • layer가 아주 많으면 입력층에 가까운 앞쪽의 layer로 갈수록 기울기의 값은 거의 0에 가깝게 작아져서 가중치의 변화가 거의 없게 되고 error값도 더 이상 줄어들지 않게 됩니다.

• 반대의 경우도 있습니다. 기울기가 점차 커지더니 가중치들이 비정상적으로 큰 값이 되면서 결국 발산되기도 합니다. 이를 기울기 폭주(Gradient Exploding) 라고 합니다.