탐색

• 여러가지 자료중 원하는 자료를 찾는 작업이다
• 탐색키(search key)
  -항목과 항목을 구별해주는 키(유일하다)
• 탐색을 위해 사용되는 자료 구조
  -배열, 연결리스트, 트리, 그래프 등

순차탐색(sequential search)

• 정렬되지 않은 배열을 처음부터 마지막까지 하나씩 검사하는 방법

시간 복잡도:O(n)

int seq_search(int key, int low, int high)
{  
int i;
for(i=low; i<=high; i++)
    if(list[i]==key)
   	return i; // 탐색 성공
return -1;    	// 탐색 실패
}

이진탐색

• 이미 정렬된 배열에서 탐색에 적합하다.
• 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지 알아내서 탐색의 범위를 반으로 줄여가며 탐색
  

int search_binary2(int key, int low, int high){
 int middle;
 while( low <= high ){ 				// 아직 키들이 남아 있으면
	middle = (low+high)/2;
	if( key == list[middle] ) return middle; 	// 탐색 성공
	else if( key > list[middle] ) low = middle+1; 	// 오른쪽 부분리스트 탐색
	else high = middle-1; 			// 왼쪽 부분리스트 탐색
 }
  return -1; 					// 탐색 실패
}

위의 코드는 반복알고리즘으로 구현

시간복잡도:O(logn)

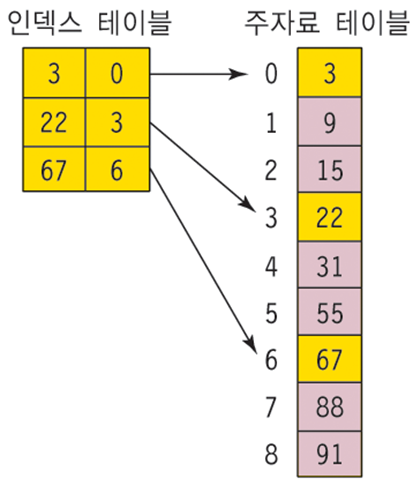
색인 순차탐색(indexed sequential search)

• 인덱스(index) 테이블을 사용하여 탐색의 효율을 증대
• 주 자료 리스트와 인덱스 테이블은 모두 정렬되어야 한다.
• 인덱스 테이블에서 index[i] <= key < index[i+1] 를 만족하는 항목만 순차탐색
• 시간복잡도: O(m+n/m) (인덱스 테이블의 크기=m, 주자료 테이블의 크기=n)

보간탐색(interpolation search)

• 사전이나 전화번호부를 탐색하는 방법
  -'ㅎ'으로 시작하는 단어는 사전의 뒷부분에서 찾음
  -'ㄱ'으로 시작하는 단어는 앞부분에서 찾음
  

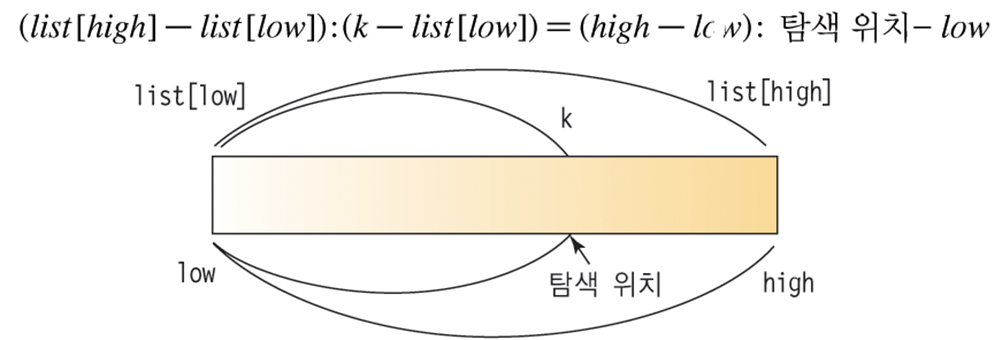
• 탐색키가 존재할 위치를 예측하여 탐색하는 방법

• 보간 탐색은 이진 탐색과 유사하나 리스트를 불균등 분할하여 탐색한다

• 시간복잡도: O(log(logn))
  
  

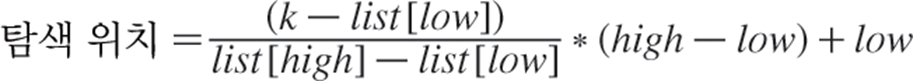
int interpol_search(int key, int n)
{
	int low, high, j;

	low = 0;
	high = n - 1;
	while ((list[high] >= key) && (key > list[low])) {
		j = (int)((float)(key - list[low]) / (list[high] - list[low]) * (high - low) + low);
		if (key > list[j]) low = j + 1;
		else if (key < list[j]) high = j - 1;
		else low = j;
	}
	if (list[low] == key) return(low);  // 탐색성공
	else return -1;  // 탐색실패
}

---

Reference C언어로 쉽게 풀어 쓴 자료구조, 천인국, 공용해, 하상호_2019