
Graph
DFS/BFS
Maze Escape
이차원 배열로 지도가 표현되어 있고, 시작점에서 끝점까지 걸리는 최단 거리를 구하는 문제이다. 이런 형식의 문제는 BFS의 논리를 가지고 풀어 가게 되지만, 일반적인 그래프를 인접 행렬 / 리스트로 표현하는 것과 다르게 각각 위치에서 주변의 4칸이 이동이 가능한지 여부를 판단하면서 풀어 나가야 한다. 이때 현재 위치에서 위 / 아래 / 왼쪽 / 오른쪽 에 해당하는 X와 Y의 차이 (델타)를 활용해서 다음 좌표를 선정하면 편하게 위치를 지정할 수 있다.
private final int[] dx = {-1, 1, 0, 0};
private final int[] dy = {0, 0, -1, 1};실제 미로는 int[][] 와 같은 방식으로 만들어 지는데, 각 좌표에 도달한적 있는지를 판단하기 위한 boolean[][] 을 같이 만들어 준다. 이 정보들을 가지고 BFS를 진행하면서 다음 과정을 판단하며 Queue에 다음 위치를 입력한다.
- 다음 위치가 범위 내에 있는지 (가로 세로를 벗어나지 않는지)
- 벽이 아닌 이동할 수 있는 공간인지
- 방문한 적 있는 공간인지
여기에 더해 문제가 최단거리 인지, 도달 가능성에 대한 건지에 대한 차이에 따라 Queue에 담기는 데이터의 형식이 조금씩 달라진다.
- 도달 가능성에 대한 문제라면 Queue가 완전히 빌 때까지 반복하면서, 목표 지점에 도달했는지 여부만 판단하면 되기 때문에 Queue에도 방문할 위치만 담기면 된다.
- 하지만 만약 최단 거리 문제라면, 현재 지점까지 오는데 얼마나 걸렸는지에 대한 데이터가 Queue에 함께 포함되어야 하며, 다음에 Queue에 데이터를 넣는 과정에서 그 데이터를 하나씩 증가시켜야 한다.
import java.util.LinkedList;
import java.util.Queue;
public class MazeEscape {
// 사방 탐색을 위한 변수
private final int[] dx = {-1, 1, 0, 0};
private final int[] dy = {0, 0, -1, 1};
// 최단 거리를 돌려 준다
public int solution(int[][] maze) {
// bfs 로직을 사용하는데
// 다음에 접근할 수 있는 칸을 maze의 가로 세로 크기 이내의 인접한 칸을 기준으로 판단
// int[]를 담는 Queue {x, y, distance}
Queue<int[]> visitNext = new LinkedList<>();
// 미로에서 이미 도달한 적 있는 칸임을 나타내기 위한 boolean[][] visited
boolean[][] visited = new boolean[6][6];
// 시작점인 (5, 0)에서 시작하고 아직 거리가 0
visitNext.offer(new int[] {5, 0, 0});
// 정답을 담기 위한 answer
int answer = -1;
// bfs 시작
// queue가 비어 있지 않은 동안에
while(!visitNext.isEmpty()) {
// 다음에 갈 곳을 queue에서 꺼낸다
int[] next = visitNext.poll();
int nowX = next[0];
int nowY = next[1];
int steps = next[2];
visited[nowX][nowY] = true;
// 네 개의 방향을 확인한다
int[] top = new int[] {nowX - 1, nowY, steps + 1}; //
for (int i = 0; i < 4; i++) {
int nextX = nowX + dx[i];
int nextY = nowY + dy[i];
// 현재 칸이 3이라면 이미 도달
// bfs이기에 제일 먼저 도달한 애가 제일 짧은 거리임을 기대할 수 있음
if (maze[nowX][nowY] == 3) {
answer = steps;
break;
}
if(
// 1. 미로의 범위를 벗어나는가?
// 2. 길이 존재하는가?
// 3. 이미 방문하지 않았는가?
(checkBounds(nextX, nextY)) &&
(maze[nextX][nextY] == 0 || maze[nextX][nextY] == 3) &&
(!visited[nextX][nextY])
) {
// 방문 대상으로 기록
visitNext.offer(new int[] {nextX, nextY, steps + 1});
// 방문 표시
visited[nextX][nextY] = true;
}
}
}
return answer;
}
// 미로의 범위 내에 있는지 검사
private boolean checkBounds(int x, int y) {
return -1 < x && x < 6 && -1 < y && y < 6;
}
public static void main(String[] args) {
// 2가 시작점 3이 목적지
// {5, 0} 시작 {0, 5} 도착
// 실제로는 x가 y 같고 y가 x처럼 움직임
int answer = new MazeEscape().solution(new int[][]{
{0, 0, 0, 0, 0, 3},
{1, 0, 1, 1, 1, 0},
{1, 0, 0, 0, 1, 0},
{1, 0, 1, 0, 1, 0},
{0, 0, 1, 0, 0, 0},
{2, 1, 1, 0, 1, 1}
});
System.out.println("answer = " + answer);
}
}이떼 boolean[][] visited 배열의 문제점을 알 수 있다. 이미 방문하려고 queue에 넣었을 경우임에도 불구하고 중복해서 queue에 들어오게 된다는 점이다. 실제로 방문했을 시점에 처리하게 되면 그렇게 된다. 따라서 queue에 넣을 때 방문 처리를 하면 중복 문제를 해결할 수 있게 된다.
Game Map Shortest Path
문제 설명
ROR 게임은 두 팀으로 나누어서 진행하며, 상대 팀 진영을 먼저 파괴하면 이기는 게임이다. 따라서, 각 팀은 상대 팀 진영에 최대한 빨리 도착하는 것이 유리하다.
지금부터 당신은 한 팀의 팀원이 되어 게임을 진행하려고 한다. 다음은 5 x 5 크기의 맵에, 당신의 캐릭터가 (행: 1, 열: 1) 위치에 있고, 상대 팀 진영은 (행: 5, 열: 5) 위치에 있는 경우의 예시이다.

위 그림에서 검은색 부분은 벽으로 막혀있어 갈 수 없는 길이며, 흰색 부분은 갈 수 있는 길이다. 캐릭터가 움직일 때는 동, 서, 남, 북 방향으로 한 칸씩 이동하며, 게임 맵을 벗어난 길은 갈 수 없다.
아래 예시는 캐릭터가 상대 팀 진영으로 가는 두 가지 방법을 나타내고 있다.
- 첫 번째 방법은 11개의 칸을 지나서 상대 팀 진영에 도착

- 두 번째 방법은 15개의 칸을 지나서 상대팀 진영에 도착

위 예시에서는 첫 번째 방법보다 더 빠르게 상대팀 진영에 도착하는 방법은 없으므로, 이 방법이 상대 팀 진영으로 가는 가장 빠른 방법이다.
만약, 상대 팀이 자신의 팀 진영 주위에 벽을 세워두었다면 상대 팀 진영에 도착하지 못할 수도 있다. 예를 들어, 다음과 같은 경우에 당신의 캐릭터는 상대 팀 진영에 도착할 수 없다.

게임 맵의 상태 maps가 매개변수로 주어질 때, 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값을 return 하도록 solution 함수를 완성해 보자. 단, 상대 팀 진영에 도착할 수 없을 때는 -1을 return 한다.
제한사항
- maps는 n x m 크기의 게임 맵의 상태가 들어있는 2차원 배열로, n과 m은 각각 1 이상 100 이하의 자연수이다.
- n과 m은 서로 같을 수도, 다를 수도 있지만, n과 m이 모두 1인 경우는 입력으로 주어지지 않는다.
- maps는 0과 1로만 이루어져 있으며, 0은 벽이 있는 자리, 1은 벽이 없는 자리를 나타낸다.
- 처음에 캐릭터는 게임 맵의 좌측 상단인 (1, 1) 위치에 있으며, 상대방 진영은 게임 맵의 우측 하단인 (n, m) 위치에 있다.
입출력 예
| maps | answer |
|---|---|
| [[1,0,1,1,1],[1,0,1,0,1],[1,0,1,1,1],[1,1,1,0,1],[0,0,0,0,1]] | 11 |
| [[1,0,1,1,1],[1,0,1,0,1],[1,0,1,1,1],[1,1,1,0,0],[0,0,0,0,1]] | -1 |
package com.example.javacodingtest.programmers.level2;
// https://school.programmers.co.kr/learn/courses/30/lessons/1844?language=java
import java.util.LinkedList;
import java.util.Queue;
public class GameMapShortestPath {
// 사방 탐색을 위한 변수
private final int[] dx = {-1, 1, 0, 0};
private final int[] dy = {0, 0, -1, 1};
// 최단 거리를 돌려 준다
public int solution(int[][] maze) {
int n = maze.length;
int m = maze[0].length;
// bfs 로직을 사용하는데
// 다음에 접근할 수 있는 칸을 maze의 가로 세로 크기 이내의 인접한 칸을 기준으로 판단
// int[]를 담는 Queue {x, y, distance}
Queue<int[]> visitNext = new LinkedList<>();
// 미로에서 이미 도달한 적 있는 칸임을 나타내기 위한 boolean[][] visited
boolean[][] visited = new boolean[n][m];
// 시작점인 (5, 0)에서 시작하고 아직 거리가 0
visitNext.offer(new int[] {0, 0, 1});
// 정답을 담기 위한 answer
int answer = -1;
// bfs 시작
// queue가 비어 있지 않은 동안에
while(!visitNext.isEmpty()) {
// 다음에 갈 곳을 queue에서 꺼낸다
int[] next = visitNext.poll();
int nowX = next[0];
int nowY = next[1];
int steps = next[2];
visited[nowX][nowY] = true;
// 네 개의 방향을 확인한다
int[] top = new int[] {nowX - 1, nowY, steps + 1}; //
for (int i = 0; i < 4; i++) {
int nextX = nowX + dx[i];
int nextY = nowY + dy[i];
// 현재 칸이 3이라면 이미 도달
// bfs이기에 제일 먼저 도달한 애가 제일 짧은 거리임을 기대할 수 있음
if (nowX == n - 1 && nowY == m - 1) {
answer = steps;
break;
}
if(
// 1. 미로의 범위를 벗어나는가?
// 2. 길이 존재하는가?
// 3. 이미 방문하지 않았는가?
(checkBounds(nextX, nextY, n, m)) &&
(maze[nextX][nextY] == 1) &&
(!visited[nextX][nextY])
) {
// 방문 대상으로 기록
visitNext.offer(new int[] {nextX, nextY, steps + 1});
// 방문 표시
visited[nextX][nextY] = true;
}
}
}
return answer;
}
// 미로의 범위 내에 있는지 검사
private boolean checkBounds(int x, int y, int n, int m) {
return -1 < x && x < n && -1 < y && y < m;
}
public static void main(String[] args) {
// 2가 시작점 3이 목적지
// {5, 0} 시작 {0, 5} 도착
// 실제로는 x가 y 같고 y가 x처럼 움직임
int answer = new GameMapShortestPath().solution(new int[][]{
{1, 0, 1, 1, 1},
{1, 0, 1, 0, 1},
{1, 0, 1, 1, 1},
{1, 1, 1, 0, 1},
{0, 0, 0, 0, 1}
});
System.out.println("answer = " + answer);
}
}Target Number
문제 설명
n개의 음이 아닌 정수들이 있습니다. 이 정수들을 순서를 바꾸지 않고 적절히 더하거나 빼서 타겟 넘버를 만들려고 한. 예를 들어 [1, 1, 1, 1, 1]로 숫자 3을 만들려면 다음 다섯 방법을 쓸 수 있다.
1+1+1+1+1 = 3 +1-1+1+1+1 = 3 +1+1-1+1+1 = 3 +1+1+1-1+1 = 3 +1+1+1+1-1 = 3
사용할 수 있는 숫자가 담긴 배열 numbers, 타겟 넘버 target이 매개변수로 주어질 때 숫자를 적절히 더하고 빼서 타겟 넘버를 만드는 방법의 수를 return 하도록 solution 함수를 작성해 보자.
제한사항
- 주어지는 숫자의 개수는 2개 이상 20개 이하
- 각 숫자는 1 이상 50 이하인 자연수
- 타겟 넘버는 1 이상 1000 이하인 자연수
입출력 예
| numbers | target | return |
|---|---|---|
| [1, 1, 1, 1, 1] | 3 | 5 |
| [4, 1, 2, 1] | 4 | 2 |
public class TargetNumber {
private int answer = 0;
public int solution(int[] numbers, int target) {
dfs(numbers, 0, target, 0);
return answer;
}
// 재귀 함수 dfs
public void dfs(
// 내가 사용할 숫자들
int[] numbers,
// 내가 다음에 사용할 차례의 숫자
// 이번 dfs 호출에서 더하거나 빼거나 할 숫자는 numbers[next]
int next,
// 목표값
int target,
// 이번 재귀까지 합한 값
int sum
) {
// 마지막 숫자를 쓴 시점에 next는 배열의 크기와 동일해진다
if(next == numbers.length) {
// target과 일치하는지 확인
if(sum == target) this.answer++;
}
else {
// 더한 다음 다음 숫자 결정
dfs(numbers, next + 1, target, sum + numbers[next]);
// 뺀 다음 다음 숫자 결정
dfs(numbers, next + 1, target, sum - numbers[next]);
}
}
public static void main(String[] args) {
int answer = new TargetNumber().solution(new int[] {1, 1, 1, 1, 1}, 3);
System.out.println("answer = " + answer);
}
}Disjoint
Disjoint
서로소 집합은 서로 중복이 포함되지 않는 즉 교집합이 존재하지 않는 집합이다. 이때 각 집합에 속한 하나의 멤버를 통해 집합을 구분하며, 연결 리스트나 트리를 이용해 표현할 수 있다.
Make Set(x): x를 대표자로 하는 집합을 생성Find Set(x): x가 속한 집합의 대표자를 반환Union(x, y): x와 y의 집합을 하나로 연합
Linked-list Implementation
연결리스트의 가장 앞 원소를 대표자로 취급해서 표현할 수 있다. 각 원소들은 대표자로 향하는 링크를 보유한다. 선형 자료 구조의 한계점이 있다.
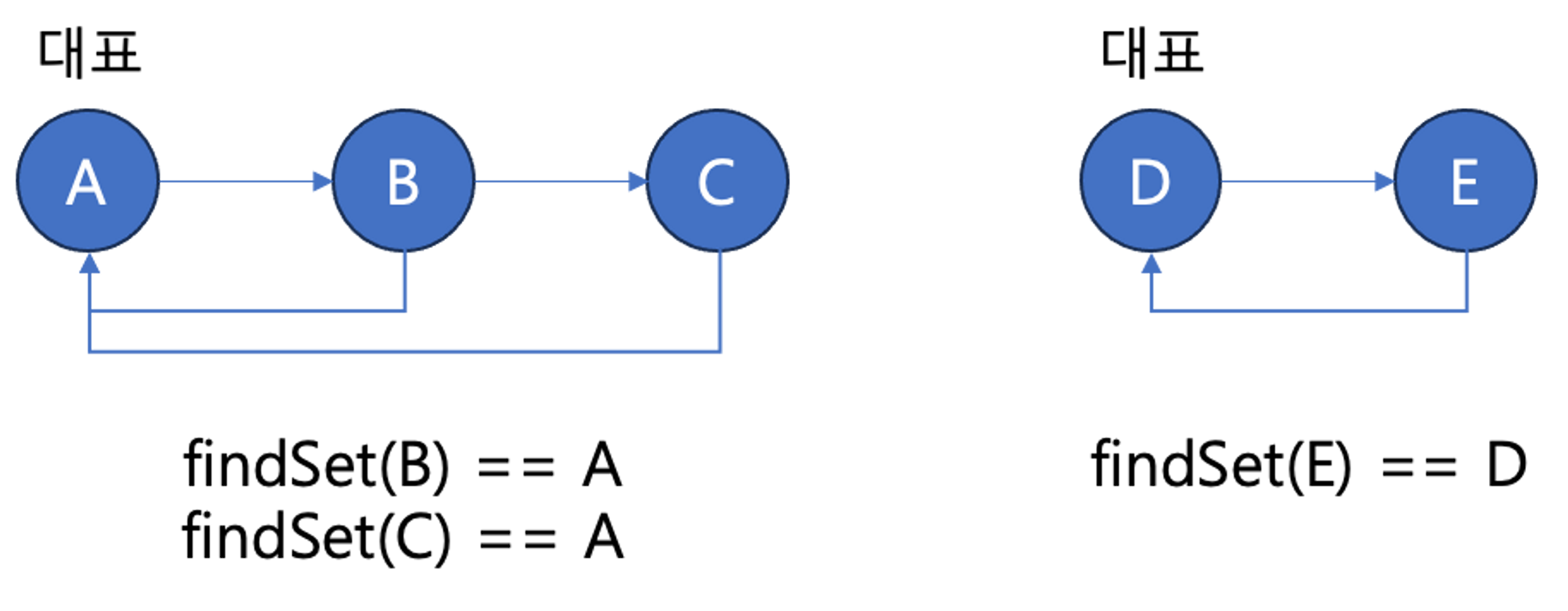
Tree Implementation
루트 노드를 대표자로 취급해서 표현할 수 있다. Find set(x)를 할 때 나 스스로가 대표가 될 때까지 재귀 호출을 하는 방식으로 함수를 작성한다.
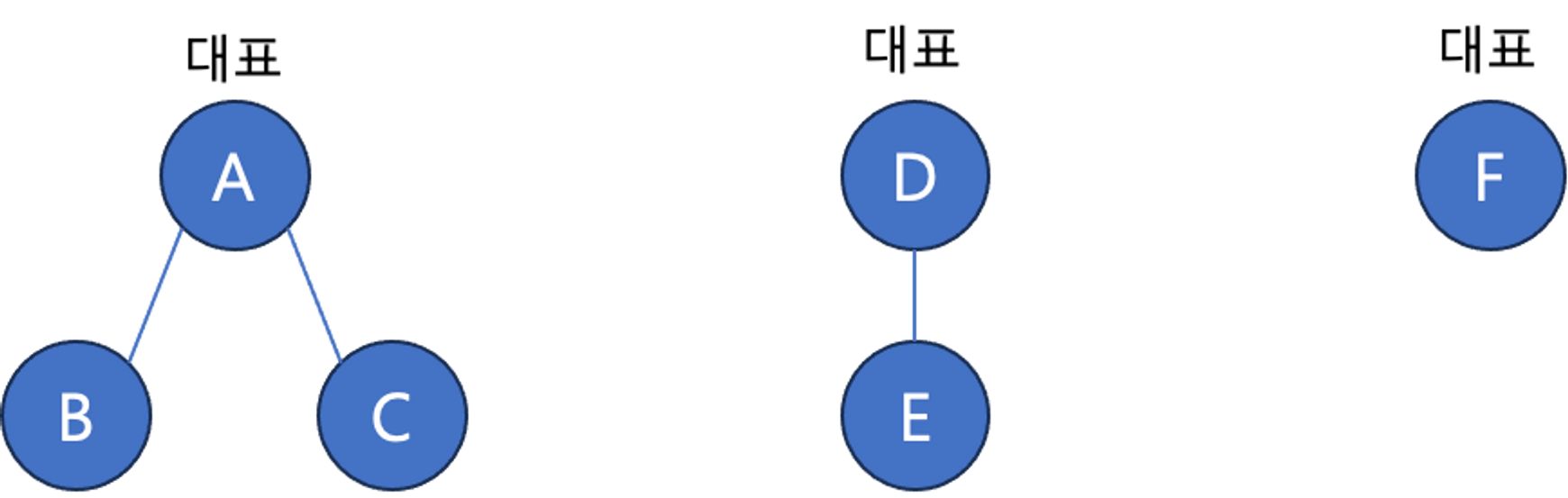
Minimun Spanning Tree
Minimun Spanning Tree
그래프의 정점과 간선 중 일부를 선택해서 구성하는 트리를 신장 트리라고 한다. 가중치 그래프일 때, 만들 수 있는 신장 트리 중 가중치 합이 최소인 트리를 최소 신장 트리라고 한다. 무향 가중치 그래프이며 사이클이 없이 n개의 정점을 모두 포함해야 한다. 예를 들어 유통망 (모두가 연결되어 있는데 비용은 최소)여야 할 때, 네트워크를 구할 때 등등 사용되는 알고리즘이다.
Kruskal Algorithm
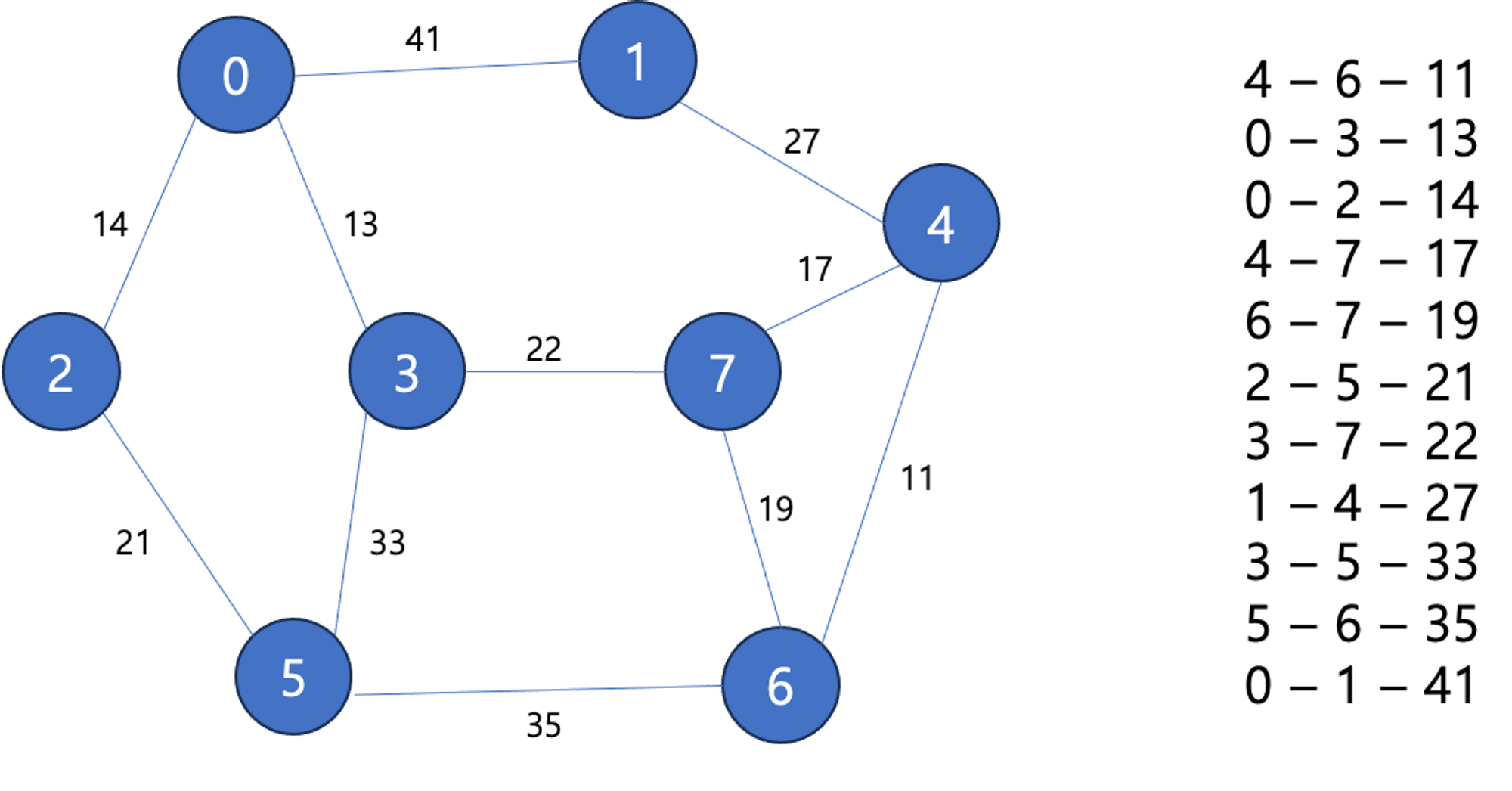
최소 신장 트리를 구하는 대표적인 알고리즘이다. 간선을 선택해가며 MST를 찾는 알고리즘이다. 노드의 갯수가 N개 일 때,
- 간선들을 가중치에 따라 오름차순으로 정렬한다.
- 가중치가 낮은 간선부터 선택하면서 트리를 만들어 간다. 이때 사이클이 존재하면, 다음으로 가중치가 낮은 간선을 선택한다.
- 선택한 간선이 N-1개가 될 때까지 선택한다.
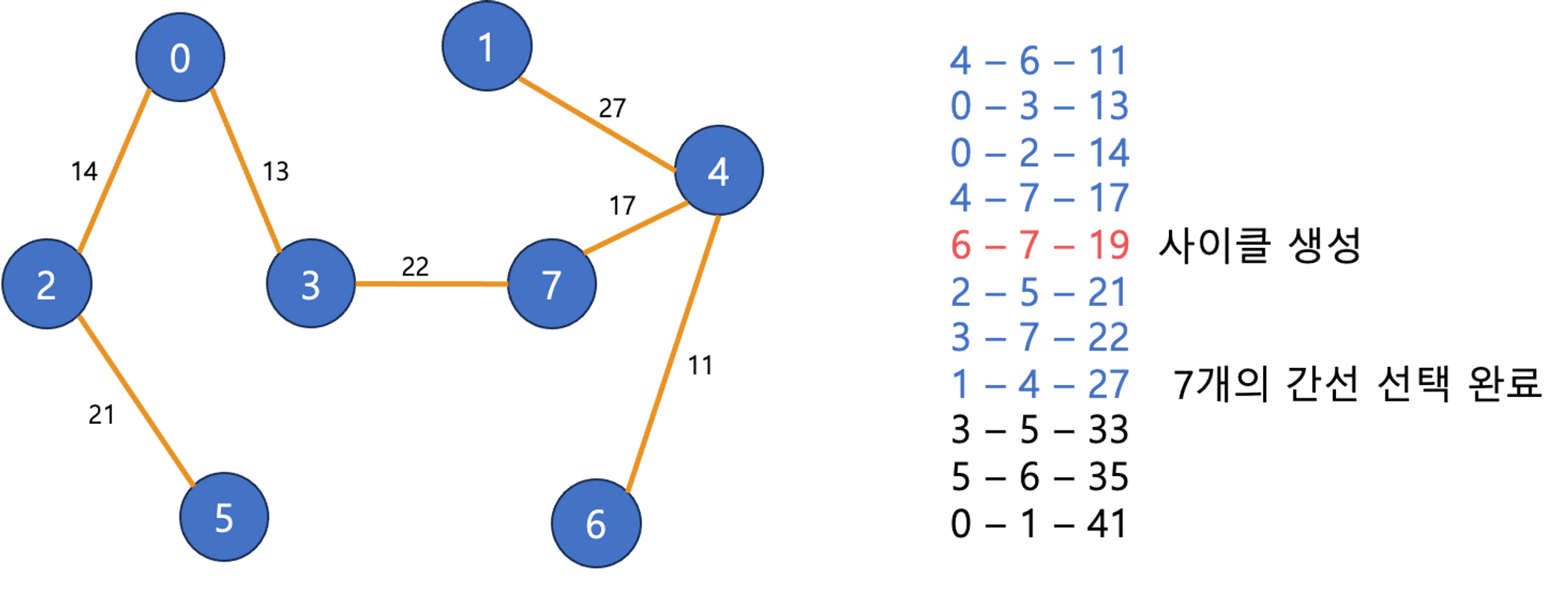
이때 사이클이 존재하는지에 대한 여부는 다음에 선택할 간선의 노드를 기준으로 찾는데, 간선에 연결된 노드가 각각 같은 집합에 속하는 경우 사이클이 생성된다고 판단하고 넘어갈 수 있다.
이때 사이클이 있는지를 판단하는 것은 서로소 집합의 개념을 활용해서 할 수 있다. 현재에 있는 노드의 루트 노드와 다음에 선택할 가장 작은 간선의 루트 노드가 같아서 같은 집합에 속하게 된다는 것을 확인하면 사이클이 생성된다는 것을 알 수 있다.
Aspect Oriented Programming
Aspected Oriented Programming
Aspected Oriented Programming
여태까지 개발한 것은 직접적인 비즈니스 로직에 해당한다. 여러 비즈니스 로직에 동일하게 작동하는 기능을 만들고 싶다면 메소드 실행의 걸린 시간이나 메소드의 반환값을 고려해야 한다. 서로 다른 비즈니스 로직이 공통적으로 가졌으면 하는 기능은 횡단 관심이다. 예를 들어 게시글을 게시하거나 댓글을 달 때 service.add는 둘 다 필요하다. 이 기능이 횡단 관점의 관심사인 것이다.
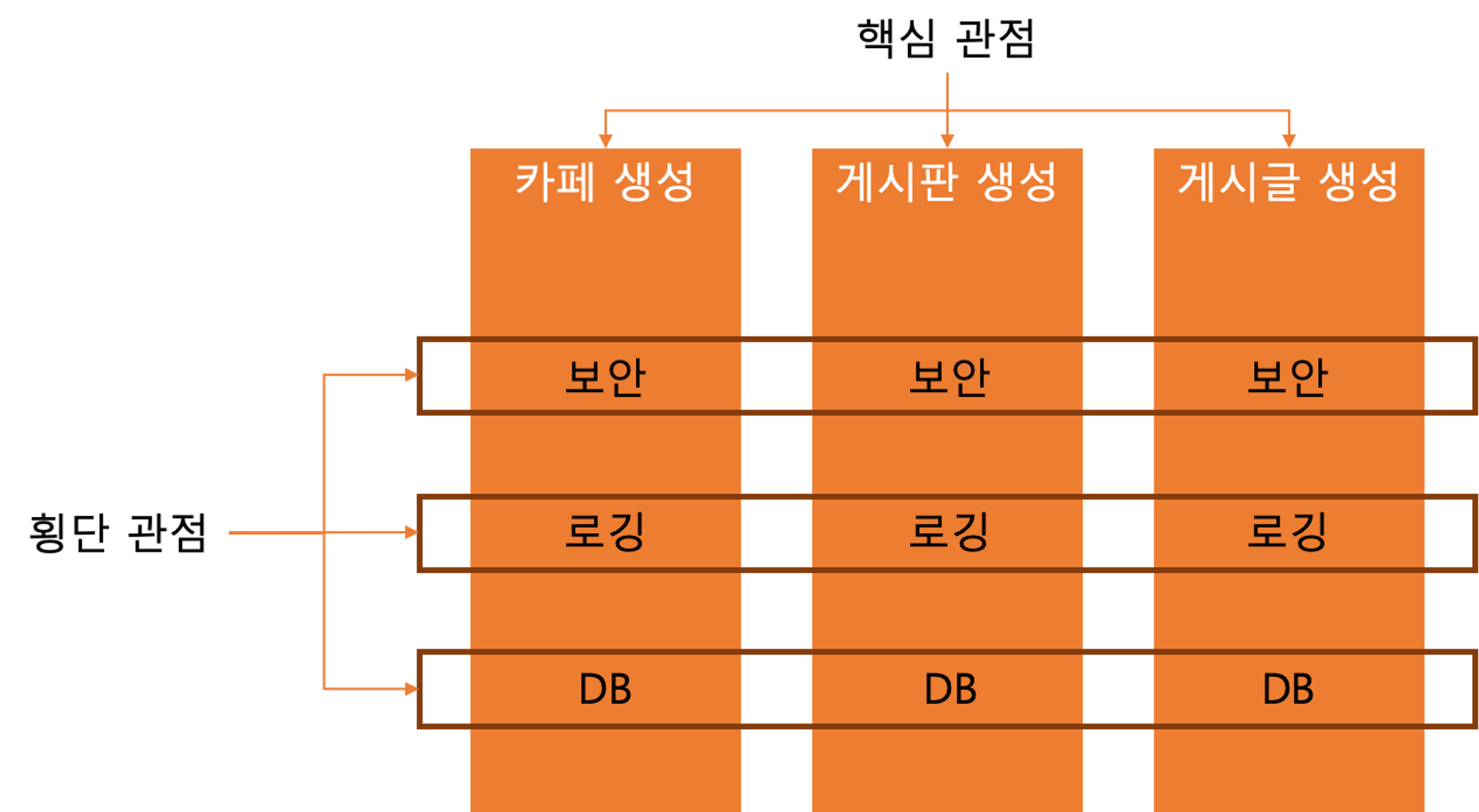
관점 지향 프로그래밍은 핵심 기능을 관리하는 코드는 건드리지 않으면서 여러 핵심 기능들이 활용할 수 있는 기능을 만드는데 초점을 맞추고 있다. 그래서 로깅과 같은 단순한 목적을 위해 소스 코드의 여러 부분에 흩어진 중복된 코드를 작성할 필요를 줄여 준다.
spring-boot-starter-aop
Spring Boot를 사용하는 경우 spring-boot-starter-aop 의존성을 추가해서 AOP 프로그래밍을 진행할 수 있다. 다만 [start.spring.io](http://start.spring.io) 에서는 추가할 수 없는데, 이는 이 이슈에서 이유를 확인할 수 있다. 그래서 저희가 활용하고자 한다면, 수동으로 의존성을 추가해 주어야 한다.
implementation 'org.springframework.boot:spring-boot-starter-aop'본격적으로 AOP를 진행하기 전에 사용하는 용어를 잠시 살펴보자.

일반적인 프로그램이 실행될 때 main의 실행 후 객체가 생성되고 죽으면서 플로우를 만들어 간다. 프로그램이 시작되고 종료될 때까지 프로그램 실행 단위마다 틈이라고 하는 Join Points가 있다. 이 부분에 관점 지향 프로그래밍 코드가 삽입되는 것이다.
Aspect: 횡단 관점에 적용할 기능을 모듈화한 단위이다. 즉 어떤 핵심 기능에 추가할 횡단 기능에 대한 정의를 담는다.Join Point: 실행 중인 프로그램에서 메소드 호출, 예외 발생 등의 시점을 지칭하는 말이다. 이러한 Join Point에 저희가 정의한 Aspect를 적용할 수 있다. 횡단 관심사가 진입할 수 있는 포인트를 말한다.Advice: 특정 Join Point에서 실제로 실행할 기능을 나타낸다. 이때 Advice는 Join Point의 전(Before), 후(After), 전후(Around) 등 다양한 시점을 지칭할 수 있다.Pointcut: 어느 특정한 Join Point를 지칭하기 위한 기준이다. Advice가 실제로 적용될 Join Point를 정의하는 역할이다. (어떤 클래스의 메소드인지 등)
@Aspect
관점을 정의하기 위해 Controller와 Dto를 하나씩 생성한다.
@Data
public class UserDto {
private Long id;
private String username;
private String password;
private String passwordCheck;
private String email;
private String phone;
}@Data
public class ResponseDto {
private String message;
}@Slf4j
@RestController
public class AopController {
public ResponseDto addUser(@RequestBody UserDto user){
userService.addUser();
ResponseDto response = new ResponseDto();
response.setMessage("success");
return response;
}
}이제 간단한 로그 기능을 통합하기 위해 LoggindAspect 클래스를 만들어 준다. Aspect임을 나타내기 위한 @Aspect 와 Spring Bean으로 등록하기 위한 @Component 가 첨부되어 있다. 이 두 가지가 있어야 저희가 Aspect 내부에 작성하는 Advice가 정상적으로 동작한다.
@Slf4j // log 추가
@Aspect // 이 클래스가 관점임을 나타냄
@Component // bean 객체로 등록
public class LogginAspect {
}이후 다음과 같은 메소드를 하나 정의한다.
@Slf4j // log 추가
@Aspect // 이 클래스가 관점임을 나타냄
@Component // bean 객체로 등록
public class LogginAspect {
// 컨트롤러 클래스의 풀 네임
// @Before: Advice, 실제로 실행될 코드를 나타냄
// @Before.value: Pointcut Designator, 어느 Joint point에서 실행될 것인지
@Before("this(com.example.aop.controller.AopController)")
public void logParameter(JoinPoint joinPoint) {
log.info("hello aop!");
}
}테스트 삼아 요청을 보내 보면 로그가 잘 찍히는 것을 볼 수 있다.

이제 이름에 맞춰서 파라미터를 로깅하는 함수로 변경해 보자.
@Slf4j // log 추가
@Aspect // 이 클래스가 관점임을 나타냄
@Component // bean 객체로 등록
public class LoggingAspect {
// 컨트롤러 클래스의 풀 네임
// @Before: Advice, 실제로 실행될 코드를 나타냄
// @Before.value: Pointcut Designator, 어느 Joint point에서 실행될 것인
// AopController가 실행되는 시점에 로그가 작동
@Before("this(com.example.aop.controller.AopController)")
public void logParameter(JoinPoint joinPoint) {
// 실행된 메소드의 정보를 담는 객체
MethodSignature methodSignature =
(MethodSignature)joinPoint.getSignature();
log.info(methodSignature.getName());
Object[] arguments = joinPoint.getArgs();
// 인자가 없을 때
if (arguments.length ==0) {
log.info("no args");
}
for (Object argument : arguments) {
log.info("argument: [{}]", arguments);
}
}
}@Before: 이 메소드가 Advice이며, 어떤 특정 Join Point 이전에 실행되는 Advice임을 나타내는 어노테이션이다."this(com.example.aop.AopController)":@Before등의 어노테이션에 전달하여 PointCut을 지정하기 위한 문법의 일부이다. 이를 Pointcut Designator라고 부른다. 여기서this는 전달된 클래스를 지정하며, 전달받은 클래스를 기준으로 작동하도록 전달하는 Designator 이다.JoinPoint: 이 Advice가 실행된 Join Point에 대한 정보가 담긴 객체이다.MethodSignature: 실행된 메소드의 정보를 담는 객체다. 여기서 메소드 이름 등 다양한 정보를 확인할 수 있다.
Postman 요청으로 확인해 보자.

Pointcut Designator
Advice를 적용하기 위해서는 어떤 JoinPoint에 적용하기 위한 것인지를 정의하기 위한 Pointcut Designator를 정의해 볼 수 있다. 몇 가지 예시만 살펴보자.
execution: 메소드를 지정한다. 이때, 클래스 내부의 메소드를 직접 지정할 수도 있지만, 클래스 내부의 메소드 전부를 지정하도록 할 수도 있다.@Before("execution(public " + "com.example.aop.dto.ResponseDto " + "com.example.aop.AopController.**addUser**(" + "com.example.aop.dto.UserDto))") // 접근 제어자 + 반환값 풀 네임 + 함수 이름 풀 네임 + 인자 풀 네임 // 또는 @Before("execution(public " + "com.example.aop.dto.ResponseDto " + "com.example.aop.AopController.***(..)**)")within: 특정 클래스를 지정한다. 클래스가 아니라 패키지 단위로 지정할 수도 있다.@Before("within(com.example.aop.AopController)") // 또는 @Before("within(com.example.aop..*)")@annotation: 어떤 특정 어노테이션이 붙은 Join Point를 지정한다. 이 어노테이션은 직접 제작할 수 있다.@Before("@annotation(com.example.aop.aspects.logging.LogArguments)")Interceptor & Filter
Interceptor & Filter
HandlerInterceptor: Spring Framework의 일부분으로 DispatcherServlet이 HandlerMethod로 요청을 넘기기 전에 실행하는 비즈니스 로직과 연관성이 높은 기능이다. 보통 보안이나 인증, 로그 등에 활용된다.Filter: Jakarta Servlet API의 일부분으로 DispatcherServlet에 도달하기 전에 요청을 검사할 수 있다. Spring 외부의 기능이기 때문에 예외 처리 등에서 Spring Framework의 도움을 받지 못한다.
