Techit 14th 3rd

Algorithm

N과 M 3

15651번: N과 M (3)

문제

자연수 N과 M이 주어졌을 때, 아래 조건을 만족하는 길이가 M인 수열을 모두 구하는 프로그램을 작성하시오.

• 1부터 N까지 자연수 중에서 M개를 고른 수열
• 같은 수를 여러 번 골라도 된다.

입력

첫째 줄에 자연수 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 7)

출력

한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다.

수열은 사전 순으로 증가하는 순서로 출력해야 한다.

예제 입력 1

3 1

예제 출력 1

1
2
3

예제 입력 2

4 2

예제 출력 2

1 1
1 2
1 3
1 4
2 1
2 2
2 3
2 4
3 1
3 2
3 3
3 4
4 1
4 2
4 3
4 4

예제 입력 3

3 3

예제 출력 3

1 1 1
1 1 2
1 1 3
1 2 1
1 2 2
1 2 3
1 3 1
1 3 2
1 3 3
2 1 1
2 1 2
2 1 3
2 2 1
2 2 2
2 2 3
2 3 1
2 3 2
2 3 3
3 1 1
3 1 2
3 1 3
3 2 1
3 2 2
3 2 3
3 3 1
3 3 2
3 3 3

코드

public class three15652 {
    private int n;
    private int m;
    private int[] arr;
    private StringBuilder answer;
    public void solution() throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer infoToken = new StringTokenizer(reader.readLine());
        n = Integer.parseInt(infoToken.nextToken());
        m = Integer.parseInt(infoToken.nextToken());
        // 순열 저장용 배열 생성
        arr = new int[m];
        // 정답 저장용 StringBuilder 생성
        answer = new StringBuilder();
        dfs(0);

        System.out.println(answer);
    }

    // 몇 번쨰 숫자를 고르고 있느냐
    public void dfs(int level) {
        if(level == m) {
            // 정답 저장
            for (int i = 0; i < m; i++) {
                answer.append(arr[i]).append(' ');
            }
            answer.append('\n');
        }
        else for (int i = 1; i <= n; i++) {
            arr[level] = i;
            dfs(level + 1);
        }
    }

    public static void main(String[] args) throws IOException {
        new three15652().solution();
    }
}

N과 M 4

15652번: N과 M (4)

문제

자연수 N과 M이 주어졌을 때, 아래 조건을 만족하는 길이가 M인 수열을 모두 구하는 프로그램을 작성하시오.

• 1부터 N까지 자연수 중에서 M개를 고른 수열
• 같은 수를 여러 번 골라도 된다.
• 고른 수열은 비내림차순이어야 한다.
  • 길이가 K인 수열 A가 A ≤ A ≤ ... ≤ A ≤ A를 만족하면, 비내림차순이라고 한다. 1 2 K-1 K
    

입력

첫째 줄에 자연수 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 8)

출력

한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다.

수열은 사전 순으로 증가하는 순서로 출력해야 한다.

예제 입력 1

3 1

예제 출력 1

1
2
3

예제 입력 2

4 2

예제 출력 2

1 1
1 2
1 3
1 4
2 2
2 3
2 4
3 3
3 4
4 4

예제 입력 3

3 3

예제 출력 3

1 1 1
1 1 2
1 1 3
1 2 2
1 2 3
1 3 3
2 2 2
2 2 3
2 3 3
3 3 3

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class three15652 {
    private int n;
    private int m;
    private int[] arr;
    private StringBuilder answer;
    public void solution() throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer infoToken = new StringTokenizer(reader.readLine());
        n = Integer.parseInt(infoToken.nextToken());
        m = Integer.parseInt(infoToken.nextToken());
        // 순열 저장용 배열 생성
        arr = new int[m];
        // 정답 저장용 StringBuilder 생성
        answer = new StringBuilder();
        dfs(0, 1);

        System.out.println(answer);
    }

    // 몇 번쨰 숫자를 고르고 있느냐
    public void dfs(int level, int largestPick) {
        if(level == m) {
            // 정답 저장
            for (int i = 0; i < m; i++) {
                answer.append(arr[i]).append(' ');
            }
            answer.append('\n');
        }
        else for (int i = largestPick; i <= n; i++) {
            arr[level] = i;
            dfs(level + 1, i);
        }
    }

    public static void main(String[] args) throws IOException {
        new three15652().solution();
    }
}

Dynamic Programming

Fibonacci

피보나치 수열은 수열의 K 번째의 숫자가, K - 1 번째의 숫자와 K - 2 번째의 숫자를 더한 값으로 이루어진 수열, 그리고 이 수열을 이루는 숫자를 피보나치 수라고 부른다. 이때 N번째 피보나치 수는 Fn 으로 표현하며, Fn = Fn-1 + Fn-2 가 된다. 그리고 그 정의상 피보나치 수열을 재귀적으로 구하는 함수를 구현하는 방법은 아래와 같다.

public int fiboSimple(int n) {
    if (n < 1)
        return 0;
    if (n == 1 || n == 2)
        return 1;
    return fiboSimple(n - 1) + fiboSimple(n - 2);
}

문제는 그 구현의 간단함과는 별개로, 이 메소드를 호출하게 될 경우 굉장히 많은 횟수의 메소드 호출이 일어나게 된다. 문제는 중복되는 연산이 계속해서 호출된다는 것이다.

이미 계산한 내용에 대한 결과를 메모리에 저장하고 있다면, 반복적인 연산을 계속해서 하지 않아도 된다.

Memorization

이전에 계산한 결과를 기억해서 이후 다시 그 결과를 다음 숫자를 구하는 데 활용하는 기법이다. 재귀 함수의 구조에서 계산해 본 경우를 담아 둔 결과를 같이 전달하기 때문에 입력값이 너무 크지 않은 문제에서 주로 사용한다. 이런식으로 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적 실행 속도를 빠르게 하는 기술을 Memoization 이라고 한다. 문자 그대로 해석하면 메모리에 넣기 라는 의미라고 볼 수 있다. 단점으로는 계산된 결과를 저장하기 위한 메모리 공간을 소모할 수 있다는 점을 가지고 있지만, 이미 만들어진 재귀적 구조의 해답을 가지고 있다면 비교적 간단하게 구현할 수 있다는 장점 또한 있다.

		public int fiboMemo(int n) {
        return fiboMemoRe(n, new int[n + 1]);
    }

    public int fiboMemoRe(int n, int[] memo) {
        if(n == 1 || n == 2) {
            return 1;
        }
        if(n == 0) return 0;
        else if (memo[n] == 0) // 만약 아직 없다면 이번에 구해서 기록
            memo[n] = fiboMemoRe(n - 1, memo) + fiboMemoRe(n - 2, memo);
        // memo[n] 이 있다면 해당 값이 지금 구하고 있는 n번째 피보나치 수열 값
        return memo[n];
    }

Dynamic Programming

반대로 우리는 피보나치 수열의 첫번째, 두번째 숫자를 이미 알고 있으면, 재귀적으로 문제를 풀 필요 없이 차근차근 더해 나가는 방식으로 이전에 있었던 부분 문제의 결과를 다음 문제의 해답을 구하는데 활용할 수 있다. 이런 식으로 전체 문제의 작은 부분을 해결하고 그 결과를 이용해 보다 큰 전체 문제의 해를 구하는 알고리즘 기법을 동적 계획법(Dynamic Programming)이라고 부른다.

public int fiboTab(int n) {
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;

        // 계산 결과 기록용 배열
        int[] fib = new int[n + 1];
        fib[1] = 1;
        fib[2] = 1;
        for (int i = 3; i < n + 1; i++) {
            fib[i] = fib[i - 1] + fib[i - 2];
        }
        return fib[n];
    }

Database

JOIN

나눠진 테이블을 다시 합칠 때 외래키를 기본키로 가진 테이블과 조합하여 결과를 도출하게 된다. 한쪽 테이블의 레코드에 다른 테이블의 기본키를 가리키는 외래키를 기준으로 테이블을 연결하는 행위를 JOIN이라고 한다.

INNER JOIN

앞서 CROSS JOIN 의 결과에 WHERE 절을 이용해 조건을 한정시켰는데, 이는 INNER JOIN을 통해서 동일한 결과를 구할 수 있다.

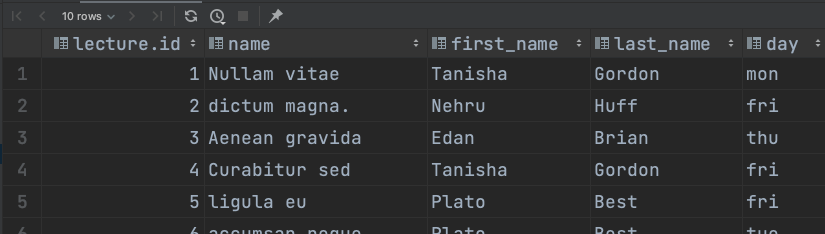
SELECT *
FROM lecture INNER JOIN instructor
    ON lecture.instructor_id = instructor.id;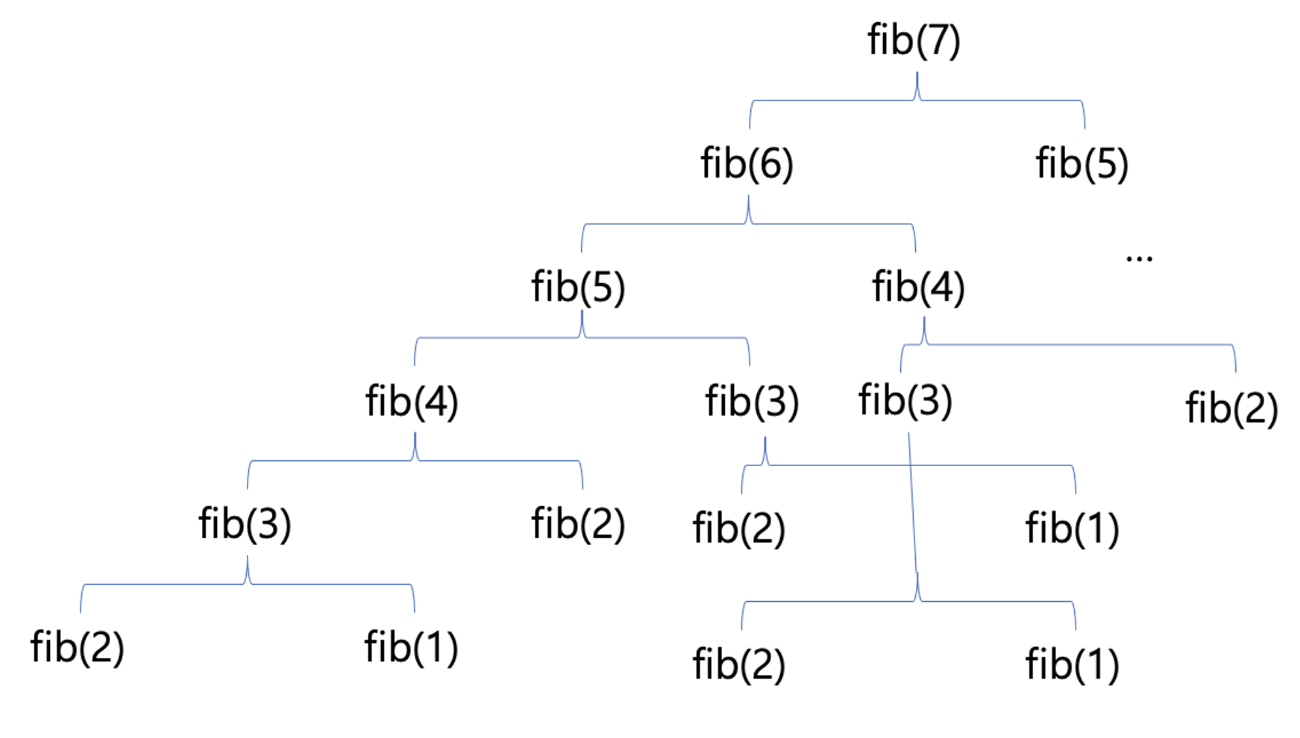

INNER JOIN 은 FROM 절 내부에서 ON 을 통해 어떤 조건을 기준으로 두 테이블을 조합할지를 전달하는 방식으로 결과를 한정지을 수 있다.

이때 조회되는 데이터의 조건이 있는데, 기본적으로 JOIN 을 진행하기 위한 조건인 lecture.instructor_id 가 일치하는 데이터만 가지고 온다. 이는 달리 말하면, 만약 instructor 테이블의 레코드 중 id 가 lecture.instructor_id 에 해당하는 동일한 값이 없는 레코드는 INNER JOIN의 결과로 확인할 수 없다는 의미이다.

그래서 주어진 결과를 다시 정리해서 [instructor.id](http://instructor.id) 를 기준으로 확인하면, 1 ~ 10 사이의 ID를 가진 instructor 의 레코드 중 일부는 찾아볼 수 없다는 걸 확인할 수 있다.

student 와 instructor 를 바탕으로 다시 확인해 보자.

SELECT *
FROM student INNER JOIN instructor
    ON student.advisor_id = instructor.id;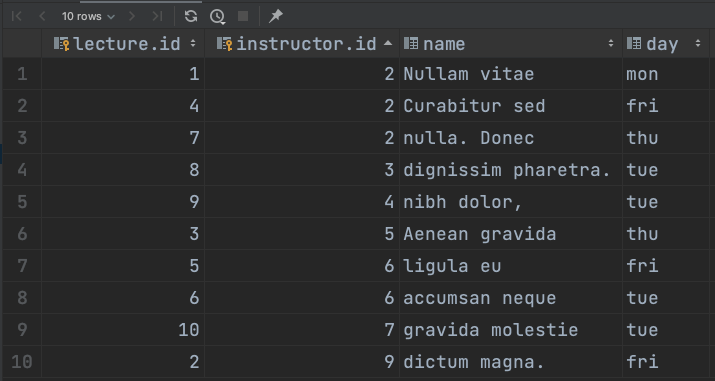

저희가 입력한 데이터는 총 20개의 student 레코드를 가지고 있지만, advisor_id 가 null 인 1 ~ 5의 레코드는 확인할 수 없다.

마지막으로, INNER 는 생략이 가능합니다. JOIN 이라고만 작성한다면 자연스럽게 INNER JOIN으로 인식하게 된다.

SELECT *
FROM lecture JOIN instructor
    ON lecture.instructor_id = instructor.id;

OUTER JOIN

만약 삭제되었거나, 비어있는 데이터라도 함께 보고 싶다면, INNER JOIN 대신 OUTER JOIN 을 활용할 수 있다. 이때 어떤 테이블을 기준으로 데이터를 보고싶은지에 따라, LEFT OUTER JOIN 과 RIGHT OUTER JOIN 으로 나뉘게 된다.

SELECT *
FROM instructor LEFT OUTER JOIN lecture
    ON instructor.id = lecture.instructor_id;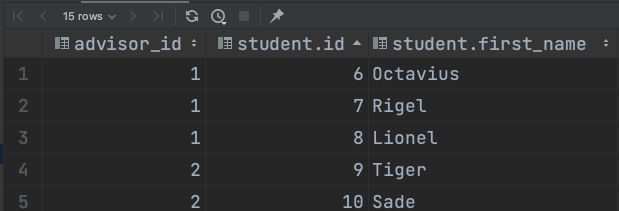

instructor LEFT OUTER JOIN lecture 을 한 결과이다. 여기서 보면 알수 있다시피, ID가 1이었던 instructor 의 레코드는 본래 연관된 lecture 가 없었어서 INNER JOIN 에서는 등장하지 않았지만, 여기서는 lecture 의 데이터 컬럼들이 null 로 대체되어 조회됨을 확인할 수 있다.

SELECT *
FROM student RIGHT OUTER JOIN instructor
    ON student.advisor_id = instructor.id;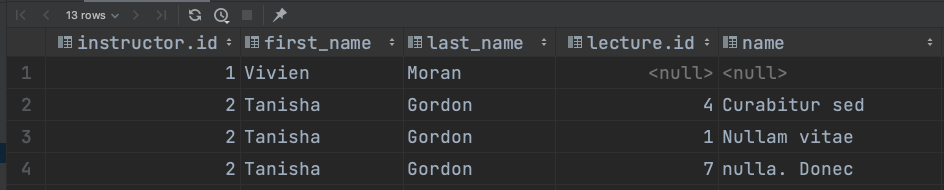

이전과 마찬가지로 student 테이블에서 연관된 레코드를 찾지 못한 경우 그 부분이 null 로 대체되어 있다. RIGHT OUTER JOIN 과 LEFT OUTER JOIN 의 기능은 거의 동일하다고 볼 수 있는데, 유일한 차이점은 앞쪽에 적은 테이블(LEFT)을 기준으로 하는지, 뒤쪽에 적은 테이블(RIGHT)을 기준으로 하는지 정도다. 어느쪽이든 그 테이블의 결과는 누락되지 않은 채 전부 조회된다.

여담으로 OUTER 는 생략이 가능하다. INNER JOIN의 경우 방향이 필요 없는 만큼, 방향이 명시되면 해당 JOIN 은 OUTER 임이 쉽게 유추 가능하다.

SELECT *
FROM instructor LEFT JOIN lecture
    ON instructor.id = lecture.instructor_id;

SELECT *
FROM student RIGHT JOIN instructor
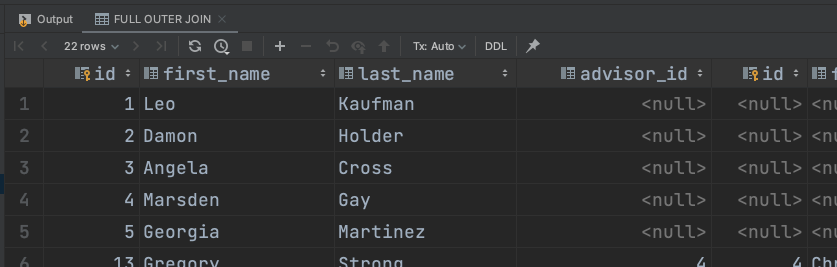
    ON student.advisor_id = instructor.id;

마지막으로 LEFT 도 RIGHT 도 아닌 FULL OUTER JOIN 이다. 이는 양쪽 모든 데이터를 확인하되, 연관관계가 없다면 없는 쪽의 컬럼은 다 null이 된다.

SELECT *
FROM student FULL OUTER JOIN instructor
   ON student.advisor_id = instructor.id;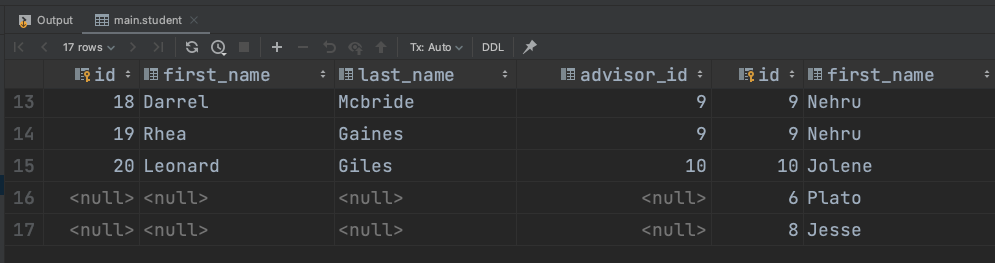

M:N

M:N 관계를 표현하고자 한다면, 한번의 FROM 절 내부에서 여러번 JOIN을 실행하면 된다.

SELECT student.id, s.first_name, s.last_name, l.name
FROM student
    INNER JOIN attending_lectures 
        ON student.id = attending_lectures.student_id
    INNER JOIN lecture 
        ON attending_lectures.attending_id = lecture.id
ORDER BY student.id;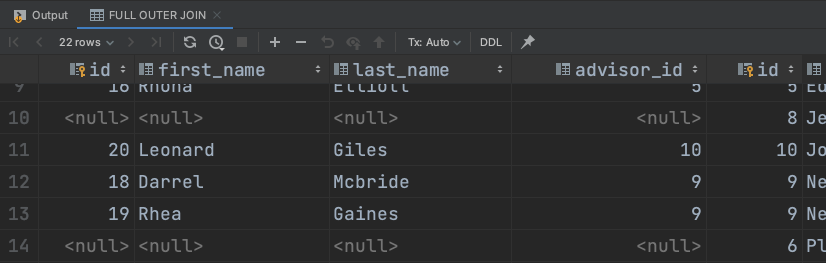

INNER JOIN 과 마찬가지로 OUTER JOIN 도 가능하다.

SELECT student.id, s.first_name, s.last_name, l.name
FROM student
    LEFT JOIN attending_lectures 
        ON student.id = attending_lectures.student_id
    LEFT JOIN lecture 
        ON attending_lectures.attending_id = lecture.id
ORDER BY student.id;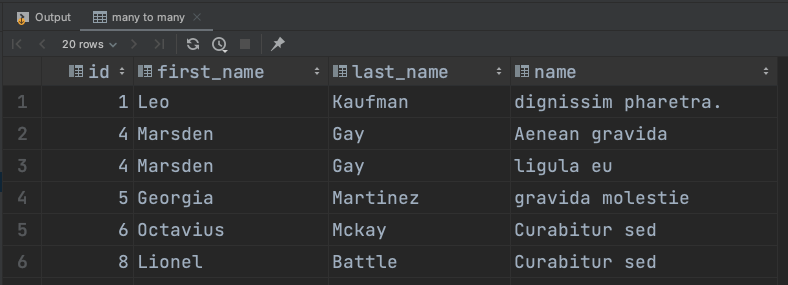

Querydsl

JpaRepository의 기능은 뭔가 아쉬워 보인다. 물론 JPQL을 사용하여 조금 더 복잡한 쿼리를 작성할 수 있지만, 문자열로 SQL 쿼리를 작성하듯이 작성해야 하기 때문에, 실제로 실행하기 전에 오류가 있는지 검사하기 어렵다.

그래서 많은 개발자들이 JPQL 대신 QueryDSL 이라는 프레임워크를 사용한다. QueryDSL은 JPQL에서는 문자열로 작성해야 하는 쿼리를 정적 타입을 이용해서 쿼리를 생성해주는 프레임워크이다.

• 문자가 아닌 코드로 쿼리를 묘사하기 때문에, 컴파일 시점에 문법 오류를 검사할 수 있다.
• 복잡한 쿼리나 동적 쿼리(주어진 데이터에 따라 런타임에 변경되는) 작성에 유리다.
• 쿼리에서 사용된 제약 조건 등을 메서드 추출을 통해 재사용하기 유리다.

먼저 의존성을 추가해 준다.