웜홀

Huisu·2023년 10월 24일

Bellman Ford Gold 3 boj

Coding Test Practice

목록 보기

52/98

문제

1865번: 웜홀

문제 설명

때는 2020년, 백준이는 월드나라의 한 국민이다. 월드나라에는 N개의 지점이 있고 N개의 지점 사이에는 M개의 도로와 W개의 웜홀이 있다. (단 도로는 방향이 없으며 웜홀은 방향이 있다.) 웜홀은 시작 위치에서 도착 위치로 가는 하나의 경로인데, 특이하게도 도착을 하게 되면 시작을 하였을 때보다 시간이 뒤로 가게 된다. 웜홀 내에서는 시계가 거꾸로 간다고 생각하여도 좋다.

시간 여행을 매우 좋아하는 백준이는 한 가지 궁금증에 빠졌다. 한 지점에서 출발을 하여서 시간여행을 하기 시작하여 다시 출발을 하였던 위치로 돌아왔을 때, 출발을 하였을 때보다 시간이 되돌아가 있는 경우가 있는지 없는지 궁금해졌다. 여러분은 백준이를 도와 이런 일이 가능한지 불가능한지 구하는 프로그램을 작성하여라.

제한 사항

첫 번째 줄에는 테스트케이스의 개수 TC(1 ≤ TC ≤ 5)가 주어진다. 그리고 두 번째 줄부터 TC개의 테스트케이스가 차례로 주어지는데 각 테스트케이스의 첫 번째 줄에는 지점의 수 N(1 ≤ N ≤ 500), 도로의 개수 M(1 ≤ M ≤ 2500), 웜홀의 개수 W(1 ≤ W ≤ 200)이 주어진다. 그리고 두 번째 줄부터 M+1번째 줄에 도로의 정보가 주어지는데 각 도로의 정보는 S, E, T 세 정수로 주어진다. S와 E는 연결된 지점의 번호, T는 이 도로를 통해 이동하는데 걸리는 시간을 의미한다. 그리고 M+2번째 줄부터 M+W+1번째 줄까지 웜홀의 정보가 S, E, T 세 정수로 주어지는데 S는 시작 지점, E는 도착 지점, T는 줄어드는 시간을 의미한다. T는 10,000보다 작거나 같은 자연수 또는 0이다.

두 지점을 연결하는 도로가 한 개보다 많을 수도 있다. 지점의 번호는 1부터 N까지 자연수로 중복 없이 매겨져 있다.

입출력 예

입력	출력
2
3 3 1
1 2 2
1 3 4
2 3 1
3 1 3
3 2 1
1 2 3
2 3 4	NO
3 1 8	YES

아이디어

최단거리를 구하는 벨만 포드 알고리즘

이때 중간에 dist[i] ≠ INF랑 비교하면 안 됨

만약 출발점이 A라면 dist[A] = 0, dist[B] = dist[C] = INF일 텐데, INF인지 비교하면 B, C는 탐색이 불가능함

해당 문제는 어디가 출발점인지 말 안 해 줘서, B, C에서 음의 사이클이 발생하는지도 봐야 함

제출 코드


import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;

public class three1865 {
    public int nodeCnt;
    public int edgeCnt;
    public List<List<int[]>> edges;
    public int[] dist;
    static final int INF = 987654321;
    public int warmholeCnt;
    public void solution() throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        int testCase = Integer.parseInt(reader.readLine());

        for (int i = 0; i < testCase; i++) {
            StringTokenizer infoToken = new StringTokenizer(reader.readLine());
            nodeCnt = Integer.parseInt(infoToken.nextToken());
            edgeCnt = Integer.parseInt(infoToken.nextToken());
            warmholeCnt = Integer.parseInt(infoToken.nextToken());

            edges = new ArrayList<>();
            for (int j = 0; j < nodeCnt; j++) {
                edges.add(new ArrayList<>());
            }

            for (int j = 0; j < edgeCnt; j++) {
                StringTokenizer edgeToken = new StringTokenizer(reader.readLine());
                int startNode = Integer.parseInt(edgeToken.nextToken()) - 1;
                int endNode = Integer.parseInt(edgeToken.nextToken()) - 1;
                int time = Integer.parseInt(edgeToken.nextToken());
                edges.get(startNode).add(new int[] {endNode, time});
                edges.get(endNode).add(new int[] {startNode, time});
            }

            for (int j = 0; j < warmholeCnt; j++) {
                StringTokenizer warmholeToken = new StringTokenizer(reader.readLine());
                int startNode = Integer.parseInt(warmholeToken.nextToken()) - 1;
                int endNode = Integer.parseInt(warmholeToken.nextToken()) - 1;
                int time = Integer.parseInt(warmholeToken.nextToken()) * (-1);
                edges.get(startNode).add(new int[]{endNode, time});
            }

            boolean minusCycle = false;
            dist = new int[nodeCnt];
            for (int j = 0; j < nodeCnt; j++) {
                if (bellmanFord(i)) {
                    minusCycle = true;
                    System.out.println("YES");
                    break;
                }
            }

            if (!minusCycle) {
                System.out.println("NO");
            }
        }
        reader.close();
    }

    private boolean bellmanFord(int start) {
        Arrays.fill(dist, INF);
        dist[start] = 0;
        boolean update = false;

        for (int i = 0; i < nodeCnt - 1; i++) {
            update = false;

            for (int j = 0; j < nodeCnt; j++) {
                for (int[] edge : edges.get(j)) {
                    if (dist[edge[0]] > dist[j] + edge[1]) {
                        dist[edge[0]] = dist[j] + edge[1];
                        update = true;
                    }
                }
            }
            if (!update) {
                break;
            }
        }

        if (update) {
            for (int i = 0; i < nodeCnt; i++) {
                for (int[] edge : edges.get(i)) {
                    if (dist[edge[0]] > dist[i] + edge[1]) {
                        dist[edge[0]] = dist[i] + edge[1];
                        return true;
                    }
                }
            }
        }
        return false;
    }

    public static void main(String[] args) throws IOException {
        new three1865().solution();
    }
}

추가 사항

Bellman-Ford Algorithm

벨만-포드 알고리즘은 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다. 간선의 가중치가 음수일 때도 최단 거리를 구할 수 있다.

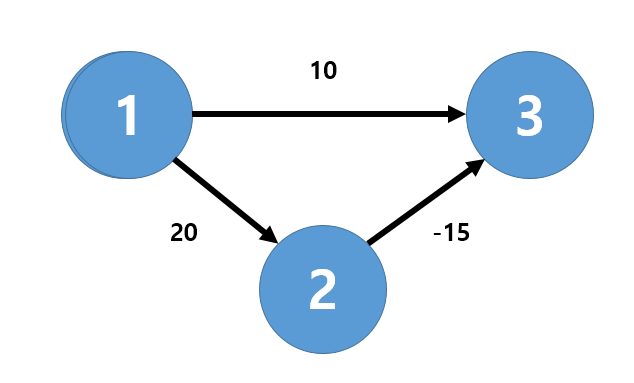
위와 같은 그림에서 노드 1에서 노드 3으로 가는 최단 거리를 구한다고 치자. 우리가 알고 있는 다익스트라 알고리즘을 쓸 경우, 노드 1에서 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드 3으로의 경로를 최단 거리로 인식한다. 그러나 노드 2와 노드 3은 음수 간선이기에 노드 1에서 노드 3으로 가는 최단 거리는 노드 1 → 노드 2 → 노드 3이다. 벨만 포드 알고리즘은 모든 간선을 매번 확인하기에 음수 간선이 있어도 찾을 수 있다.

정리하자면,

[다익스트라 알고리즘]