[프로그래머스] 조이스틱

1. 링크 프로그래머스 조이스틱

2. 풀이

조이스틱을 가로로 조작하는 경우랑 세로로 조작하는 경우 두 경우는 따로 계산해도 상관없다. 그러므로 두 경우를 따로 구해서 더해주면 된다.

1. 세로로 조작하는 경우

조작하는 알파벳으로 A에서 위쪽으로 조작하는 것이 빠른지, 아니면 A에서 아래쪽으로 조작하는 것이 빠른지 둘 다 계산을 해준 후에 빠른 경우를 택해주면 된다.

int count_minimum_character_moves(char c)
{
    int count = 'Z' + 1 - c;
    if (c - 'A' < count)
        count = c - 'A';
    return count;
}

그리고 이를 for문으로 name의 길이까지 계산하면,

int count_vertical_moves(const string& name)
{
    int total = 0;
    for (int i = 0; i < name.size(); i++)    
        total += count_minimum_character_moves(name[i]);
    return total;
}

2. 가로로 조작하는 경우

• BBBBBBAB처럼 처음부터 끝까지 가는 경우의 수

• ABAAAAABB처럼 앞으로 갔다가 뒤쪽으로 가는 것이 빠른 경우의 수

• ABBBAAAAABA처럼 뒤로 갔다가 앞쪽으로 가는 것이 제일 빠른 경우의 수

이렇게 3가지가 있습니다.

BBBBBBAB같이 처음부터 끝까지 가는 경우는 n - 1

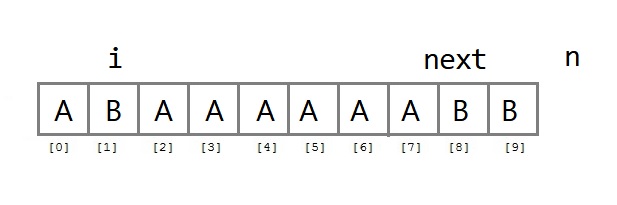
그림과 같이 앞쪽으로 갔다가 뒤쪽으로 가는 것이 빠른 경우는 2 ⨯ i + n - next = i + n - next + i

반대로, 뒤쪽으로 갔다가 앞쪽으로 가는 것이 빠른 경우는 i + 2 ⨯ (n - next) = i + n - next + (n - next)

이 두 식을 만족하는 것을 코드로 쓰면 i + n - next + min(i, n - next)가 된다.

이를 종합해서 cpp코드로 쓰면

int count_horizontal_moves(const string& name)
{
    int n = name.size();
    int total = n - 1;
    for(int i = 0; i < n; i++)
    {
        int next = i + 1;
        while(next < n and 'A' == name[next])
            next++;
        total = min(total, i + n - next + min(i, n - next));           
    }
    return total;
}

이 된다.

3. 코드

#include <string>
#include <algorithm>

using namespace std;

int count_minimum_character_moves(char c)
{
    int count = 'Z' + 1 - c;
    if (c - 'A' < count)
        count = c - 'A';
    return count;
}

int count_vertical_moves(const string& name)
{
    int total = 0;
    for (int i = 0; i < name.size(); i++)    
        total += count_minimum_character_moves(name[i]);
    return total;
}

int count_horizontal_moves(const string& name)
{
    int n = name.size();
    int total = n - 1;
    for(int i = 0; i < n; i++)
    {
        int next = i + 1;
        while(next < n and 'A' == name[next])
            next++;
        total = min(total, i + n - next + min(i, n - next));           
    }
    return total;
}

int count_minimum_moves(const string& name)
{
    int total = 0;

    total += count_vertical_moves(name);
    total += count_horizontal_moves(name);

    return total;
}


int solution(string name)
{
    return count_minimum_moves(name);
}