[BOJ. 2580] 스도쿠
1. 링크 백준 2580 스도쿠
2. 풀이
1. Brute Force
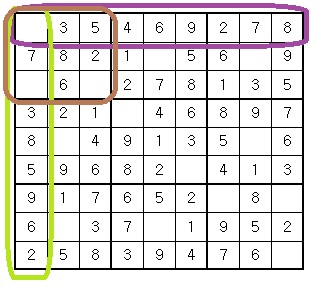
각각의 빈칸에 들어갈 숫자가 되는지 안되는지는 무차별로 대입해서 알아야 합니다.
무차별로 대입하는 방법은
- 가로에서 같은건 없는지
- 세로에서 같은건 없는지
- 3⨯3블럭에서 같은건 없는지
이렇게 총 3가지를 확인해야 합니다.
가로와 세로에서 같은 숫자가 있는지 없는지는 각각의 열(row)과 행(col)에서 loop문을 돌리면 됩니다.
bool isAvailableRow(int n, int row)
{
for (int i = 0; i < Nine; i++)
{
if (n == board[row][i])
return false;
}
return true;
}bool isAvailableColumn(int n, int col)
{
for (int i = 0; i < Nine; i++)
{
if (n == board[i][col])
return false;
}
return true;
}3⨯3블럭에서 중복이 되는 숫자가 있는지 확인하기 위해서는 현재의 열과 행을 3으로 나눈 뒤에 다시 3을 곱하면 3⨯3블럭의 시작점이 된다는 것을 이용해서 loop문을 돌리면 됩니다.
ex) (4, 5)가 있는 위치의 3⨯3블럭의 시작점은 (4 / 3 * 3, 5 / 3 * 3) = (3, 3)이다.
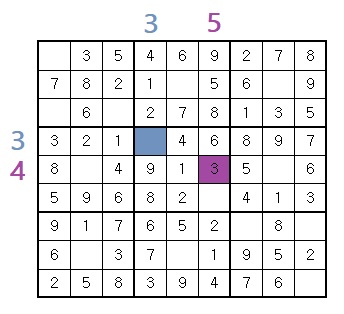
bool isAvailableBlock(int n, int row, int col)
{
int rowQuota = row / 3;
int colQuota = col / 3;
int startRow = rowQuota * 3;
int endRow = startRow + 3;
int startColumn = colQuota * 3;
int endColumn = startColumn + 3;
for (int i = startRow; i < endRow; i++)
{
for (int j = startColumn; j < endColumn; j++)
{
if (n == board[i][j])
return false;
}
}
return true;
}이렇게 가로, 세로, 3⨯3블럭을 확인하는 함수를 합해서 하나의 함수로 만들면 됩니다.
bool isAvailable(int row, int col, int n)
{
return isAvailableRow(n, row) and
isAvailableColumn(n, col) and
isAvailableBlock(n, row, col);
}2. Backtracking
각각의 조건이 만족하더라도 다음 그림과 같이 성립할 수 없는 경우가 발생할 수 있습니다.
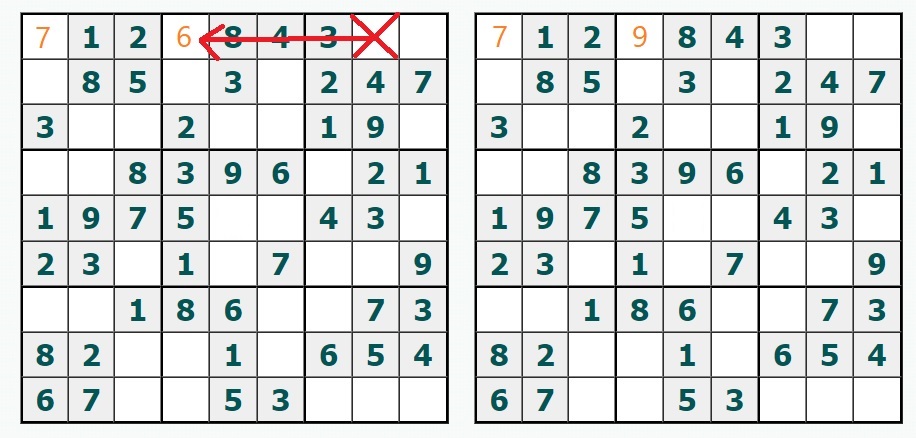
이러한 경우에는 다시 그 지점으로 돌아간 뒤에 다음 경우를 계산해주어야 합니다.
이를 하기 위해서는 DFS의 Backtracking을 사용해야 합니다.
스도쿠의 0의 행과 열이 들어가 있는 변수를 blanks로 하고 DFS의 Backtracking을 이용하여 재귀로 Pseudo code로 구현하면 다음과 같습니다.
dfs(blanks, count)
if(count == blanks.end)
isFinished = true
blankRow = blanks[count].row
blankColumn = blanks[count].column
for (int i = 1; i <= Nine; i++)
if (false == isAvailable(blankRow, blankColumn, i))
continue;
board[blankRow][blankColumn] = i;
dfs(blanks, count + 1);
if(true == isFinished)
return;
board[blankRow][blankColumn] = 0; 3. 코드
#include <iostream>
#include <vector>
#include <utility>
using namespace std;
const int Nine = 9;
int board[Nine][Nine];
void input()
{
for (int i = 0; i < Nine; i++)
{
for (int j = 0; j < Nine; j++)
{
cin >> board[i][j];
}
}
}
void print()
{
for (int i = 0; i < Nine; i++)
{
for (int j = 0; j < Nine; j++)
{
cout << board[i][j] << ' ';
}
cout << '\n';
}
}
bool isAvailableRow(int n, int row)
{
for (int i = 0; i < Nine; i++)
{
if (n == board[row][i])
return false;
}
return true;
}
bool isAvailableColumn(int n, int col)
{
for (int i = 0; i < Nine; i++)
{
if (n == board[i][col])
return false;
}
return true;
}
bool isAvailableBlock(int n, int row, int col)
{
int rowQuota = row / 3;
int colQuota = col / 3;
int startRow = rowQuota * 3;
int endRow = startRow + 3;
int startColumn = colQuota * 3;
int endColumn = startColumn + 3;
for (int i = startRow; i < endRow; i++)
{
for (int j = startColumn; j < endColumn; j++)
{
if (n == board[i][j])
return false;
}
}
return true;
}
bool isAvailable(int row, int col, int n)
{
return isAvailableRow(n, row) and isAvailableColumn(n, col) and isAvailableBlock(n, row, col);
}
void dfs(vector<pair<int, int>>& blanks, bool& isFinished, int count = 0)
{
if (blanks.size() == count)
{
isFinished = true;
return;
}
int blankRow = blanks[count].first;
int blankColumn = blanks[count].second;
for (int i = 1; i <= Nine; i++)
{
if (false == isAvailable(blankRow, blankColumn, i))
continue;
board[blankRow][blankColumn] = i;
dfs(blanks, isFinished, count + 1);
if (true == isFinished)
return;
board[blankRow][blankColumn] = 0;
}
}
void fillSudokuBlanks()
{
vector<pair<int, int>> blanks;
for (int i = 0; i < Nine; i++)
{
for (int j = 0; j < Nine; j++)
{
if (0 == board[i][j])
blanks.push_back({ i, j });
}
}
bool isFinished = false;
dfs(blanks, isFinished);
}
int main(void)
{
input();
fillSudokuBlanks();
print();
}