연쇄행렬곱셈
브루트 포스 방식
- 행렬이 N개일 때 곱셈의 종류는 Tn 가지

- 맨 마지막 곱만 남긴다고하면 1번과 3번은 같아. T(n-1) A*Z 라고 볼 수 있으니
-
결국 Tn >= 2T(n-1) (n=3 일때 같아!)
또 T2=1 -
repeated 연산으로 점화식을 깨면
Tn >=2^(n-2) => O(2^n)
=> 브루트포스로는 어렵다...
DP로
-
A1* A2* A3* A4 ....
연쇄 행렬 곱셈임으로 ixj jxk ...이라서
i =d0 j= d1 k=d2 ... 총 n+1 행 필요! -
M[i][j] 에 Ai부터 Aj까지 필요한 곱셈 최소 횟수를 저장하자
ex) M[1][n] 는 A1~ An까지 곱셈 횟수
k=1 이면 (A1)(A2A3A4A5A6)
k=2 이면 (A1A2)(A3A4A5A6) ...
최종 두개가 되는건 5개의 그룹! =>우리가 원하는 최적 값은 5개 경우 중 하나 + 선택된 그룹 내부 또한 최적의 경우일떄!
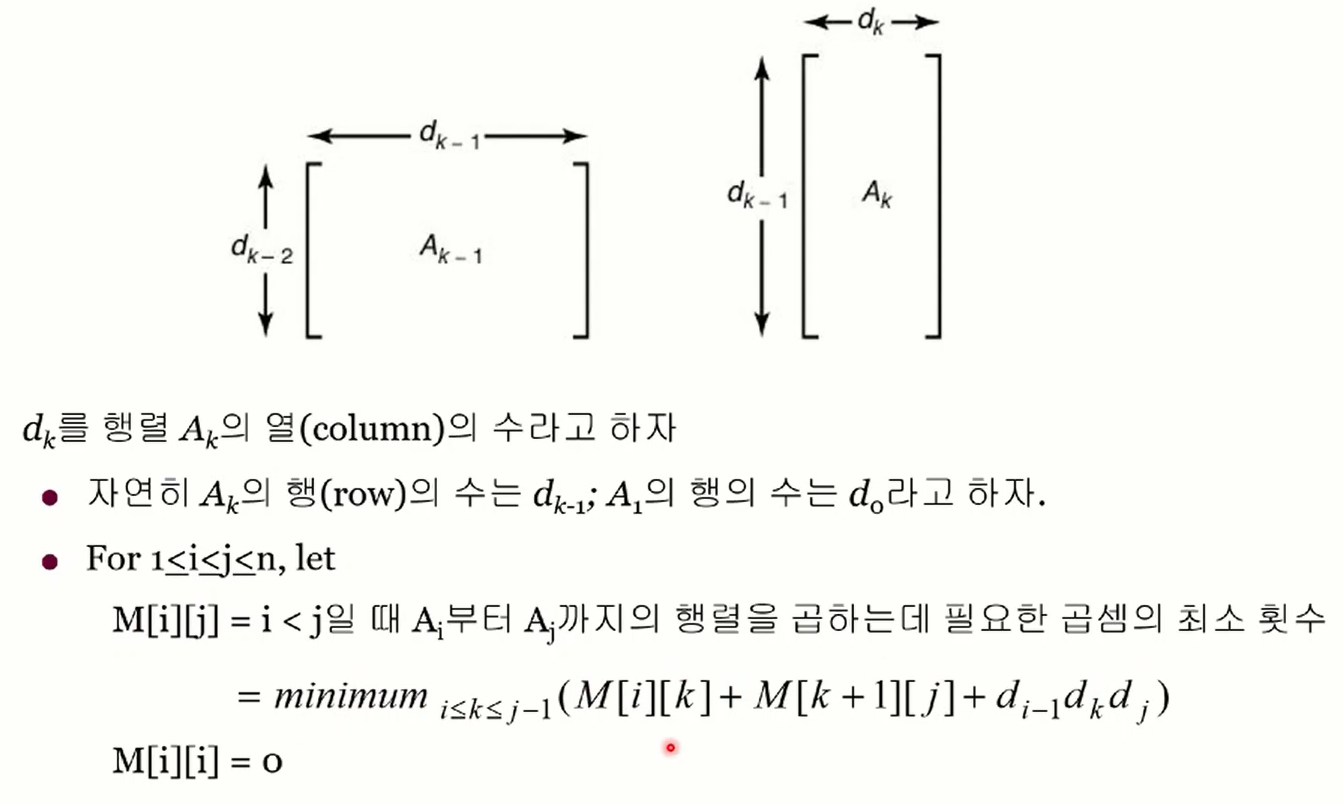
내부가 최적인 건 어차피 dp로
- Ex) n=6일때
M[1][6] = min(m[1][k]+m[k+1][6]+d0 dk d6) (1<=k<=5)
=> 첫번째 괄호부분을 하나의 행렬로 만드는 곱셈횟수 + 두번째 괄호부분... 곱셈횟수+ 이 두 행렬을 하나로 만드는 곱셈횟수
따라서 min은 k=1일떄의 최종값, k=2일때의 최종 값... 중에서 제~일 작은 값
키포인트
Ex) (A1)(A2A3A4A5A6) 일때 (A2A3A4A5A6) 얘를 부셔야 내부 최적 계산이 되지.
- (A2A3A4A5A6) => (A2)(A3~A6) , (A2A3)(A4~A6) ...
- n= 6일때 n=1을 다풀면 n=2 풀때 재료가 되고, n=3풀때 n=2푼게 재료가 돼
1개 짜리는 (A1)(A2)(A3)(A4)(A5)(A6) 이고
2개 짜리는 (A1A2) (A2A3) (A3A4) (A4A5) (A5A6)
3개 짜리는 (A1A2A3) (A2A3A4) (A3A4A5) (A4A5A6)
4개 짜리는 (A1A2A3A4) (A2~A5) (A3~A6)
5개 짜리는 (A1~A5) (A2~A6)
6개 짜리는 A1~A6
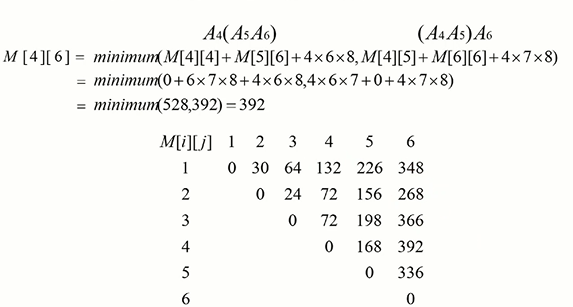
대각선으로 1개짜리 2개짜리... 해서 재료를 얻어
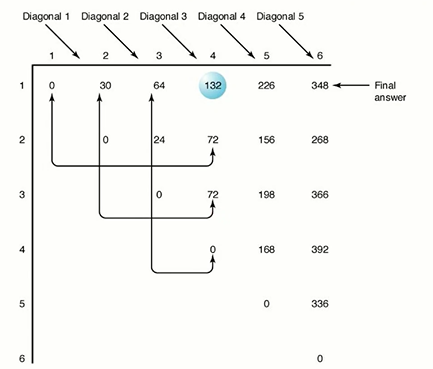
Ex) 1~4까지 부분문제 합(132)을 보자
(A1)(A2~A4),(A1A2)(A3A4),(A1A2A3)(A4) 이렇게 인데
그림에서 볼 수 있듯이 (1,1) (2,4)가 함께 참조 , (1,2)(3,4) 참조 (1,3)(4,4) 참조 인걸 볼 수 있다. 이렇기 때문에 대각선으로 채워야 유리!

행렬 n개짜리, d0~dn 까지 행렬의 열수, for문은 두개짜리 부터 푸는거.
첫 for는 대각선 하나를 결정
두번째 for에서는 행(i)를 결정. 행은 대각선이 증가하면 하나씩 -1. => n-diagonal
DP 사용의 이유
- 필요한거 부터 먼저 풀어서 재료를 만듬 => Bottom-Up 이기때문에 대각선으로 푼다.
- 부분문제의 최적합이 전체 문제 풀때 그대로 유지됨 => Optimal Substructure
성능 분석

- 3중 for문을 보면
d: 1~n-1 => n-1
i: 1~n-d => n-d
j: i~j-1 => n-1
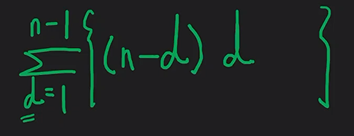
시그마를 풀면 n(n-1)(n+1)/6 => O(n^3)
최적 순서의 구축
- P[i][j] 에 M[i][j]를 계산할 때 최솟값인 k값을 저장한다.

Ex)
- P[1][6] = 1 => A1에서 나눠서 곱해야한다. (A1)(A2A3A4A5A6)
(A2A3A4A5A6) 는 어떻게 곱하지? - P[2][6] = 5 => A2~A6까지는 A5에서 나눠서 곱하고 마지막에 A1이랑 곱해야한다. (A1)(A2A3A4A5)(A6)
(A2A3A4A5) 는 어떻게 곱하지? - P[2][5] = 4 => A2~A5까지는 A4에서 나눠서 곱해야한다. A2~4와 나눠서 곱해 (A1)(A2A3A4)(A5)(A6)
(A2A3A4) 는 어떻게 곱하지? - P[2][4] = 3 => A2~A4까지는 A3에서 나눠서 곱해야한다.
(A1)(A2A3)(A4)(A5)(A6)
이런식으로 재귀함수가 형성된다

참고로 P 함수 알고리즘만 놓고 O(n)임
